各种二叉树的介绍

数据结构中有很多种类的树结构，例如，普通二叉树、完全二叉树、满二叉树、线索二叉树、哈夫曼树、二叉搜索树（排序树）、平衡二叉树、AVL平衡二叉树、红黑树、B树、B+树、堆

1、普通二叉树、完全二叉树、满二叉树

二叉树：最多有两棵子树的树被称为二叉树

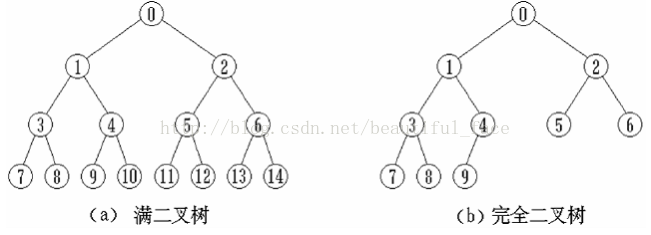
满二叉树：二叉树中所有非叶子结点的度都是2，且叶子结点都在同一层次上

完全二叉树：如果一个二叉树与满二叉树前m个节点的结构相同，这样的二叉树被称为完全二叉树

也就是说，如果把满二叉树从右至左、从下往上删除一些节点，剩余的结构就构成完全二叉树

采用顺序存储的完全二叉树，可以根据任意节点的位置计算其父节点、孩子节点在数组中的位置（下标），如果父节点和孩子节点存在的话。

这也说明，完全二叉树适合使用顺序表存储

 

2、线索二叉树

关于树的一些小知识点

 

3、哈夫曼树（最优二叉树）

Huffman树及JAVA实现 

4、二叉搜索（查找、排序）树

定义：

二叉查找树，也叫二叉排序树是满足以下条件的二叉树：
1.左子树上的所有节点值均小于根节点值
2.右子树上的所有节点值均不小于根节点值
3.左右子树也满足上述两个条件

二叉查找树（华中科技大学计算机考研复试上机题）

对二叉树进行中序遍历时，其输出是一个有序数组

根据二叉排序树的定义，发现其搜索过程具有二分特性，效率较高

缺点：二叉排序树的最终形态与输入数据的顺序有关，

例如，输入数据[1,2,3,4,5,6,7,8,9]，最终形成的二叉排序树如下图

此时，二叉树退化成了单链表，查找效率大大下降

5、平衡二叉树

为了克服二叉排序树的缺点，人们想出办法，使得一棵树的左右子树高度大致相等

比较出名的是苏联科学家家G.M. Adelson-Velsky 和 E.M. Landis于1962年提出的,被命名为AVL树，，和红黑树

 

6、AVL树

任一节点的左子树深度和右子树深度相差不超过1，我们用平衡因子衡量这种差异

任意节点的平衡因子Balance(p)= heigth(p的左子树) - height（p的右子树）

在进行AVL树的插入和删除操作时，当平衡因子=2时，就要调整节点的位置，使其满足AVL树的定义

关于AVL树的插入、删除操作，随后会进行记录 

7、红黑树 

性质1. 节点是红色或黑色。

性质2. 根节点是黑色。

性质3 每个叶节点（NIL节点，空节点）是黑色的。

性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

红黑树 阿里特别看重，我做了总结

参考：红黑树之 原理和算法详细介绍(阿里面试-treemap使用了红黑树) 红黑树的时间复杂度是O(lgn) 高度<=2log(n+1)1、X节点左旋-将X右边的子节点变成 父节点 2、X节点右旋-将X左边的子节点变成父节点

 

总结：我们知道，实际应用当中，我们经常使用的是查找和排序操作，这在我们的各种管理系统、数据库系统、操作系统等当中，十分常用。

数组的下标寻址十分迅速，但计算机的内存是有限的，故数组的长度也是有限的，实际应用当中的数据往往十分庞大

而且无序数组的查找最坏情况需要遍历整个数组

后来人们提出了二分查找，二分查找要求数组的构造一定有序。二分法查找解决了普通数组查找复杂度过高的问题

任和一种数组无法解决的问题就是插入、删除操作比较复杂，因此，在一个增删查改比较频繁的数据结构中，数组不会被优先考虑

普通链表由于它的结构特点被证明根本不适合进行查找

二叉查找树因为可能退化成链表，同样不适合进行查找

哈希表是数组和链表的折中，，同时它的设计依赖散列函数的设计，数组不能无限长、链表也不适合查找，所以也适合大规模的查找

AVL树的旋转过程非常麻烦，因此插入和删除很慢，也就是构建AVL树比较麻烦

红黑树是平衡二叉树和AVL树的折中，因此是比较合适的。集合类中的Map、关联数组具有较高的查询效率，它们的底层实现就是红黑树

参考：查找（一）史上最简单清晰的红黑树讲解

参考：红黑树