红黑树原理以及插入、删除算法 附图例说明

一、概念

R-B Tree，全称是Red-Black Tree又称红黑树，它是一种特殊的二叉查找树，红黑树的每个节点上都有存储位表示节点的颜色，可以是红或黑。

二、特性

1、每个节点或者是红色，或者是黑色

2、根节点是黑色的

3、每个叶子节点（NIL）是黑色的。注意：这里的叶子节点，是指为空的叶子节点

4、如果一个节点是红色的，则它的子节点必须是黑色的

5、从任意一个节点到其叶子的所有路径中，所包含的黑节点数量是相同的

特性解析1：根据特性4可知，从每个叶子节点到根节点的所有路径中不能有两个连续的红节点

特性解析2：根据特性5可知，没有一条路径会比其它路径长出两倍，因而红黑树是接近平衡的二叉树

三、应用

红黑树主要用于存储有序的数据，它的时间复杂度是O(logn)，非常高效

四、基本操作——插入

1、简介

红黑树的基本操作是添加和删除，在对红黑树进行添加和删除之后，都会用到旋转方法。为什么要用旋转方法呢？因为添加或删除红黑树的节点之后，红黑树就发生了变化，可能就不满足红黑树的5条性质了，也就不是一颗红黑树了。而通过旋转可以使这棵树重新成为红黑树，即旋转的目的就是为了保证红黑树的特性

左旋：对节点x进行左旋，意味着将“x的右孩子变成x的父亲”，而将“x原先的右孩子的左孩子变成x的右孩子”。即左旋中的“左”是指将别旋转的节点变成一个左节点

右旋：对节点x进行右旋，意味着将“x的左孩子变成x的父亲，而将”x原先的左孩子的右孩子变成x的右孩子“。即右旋中的”右“是指将被旋转的节点变成一个右节点

2、插入规则

新插入的节点都为红色

3、红黑树插入的4种情形

（1）新节点位于根节点，其没有父节点时，处理思路：将该节点直接设为黑色即可

（2）新节点的父节点已然是黑色时，处理思路：不用动，这已然是一颗红黑树

（3）父节点和叔节点都是红色时，处理思路：a.将父节点和叔节点设为黑色;b.将祖父节点设为红色;c.将祖父节点设为当前节点，并继续对新当前节点进行操作

（4）父节点是红色，叔节点是黑色时，又分如下四种情况：

• 当前节点是父亲的左孩子，父亲是祖父的左孩子（Left-Left），处理思路：a.将祖父节点右旋;b.交换父节点和祖父节点的颜色
• 当前节点是父亲的右孩子，父亲是祖父的左孩子（Right-Left），处理思路：a.将父节点左旋，并将父节点作为当前节点; b.然后再使用Left Left情形
• 当前节点是父亲的右孩子，父亲是祖父的右孩子（Right-Right），处理思路：a.将祖父节点左旋;b.交换父节点和祖父节点的颜色
• 当前节点是父亲的左孩子，父亲是祖父的右孩子（Left-Right），处理思路：a.将父节点右旋，并将父节点作为当前节点; b.然后再使用Right Right情形

4、插入图例

通过插入12   1   9   2   0   11   7   19   4   15   18   5   14   13   10   16   6   3   8   17完成上述所有情形的展示。

（1）插入12

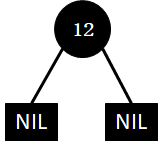
说明：插入的节点若是根节点，则直接将其设置为黑色

（2）插入1

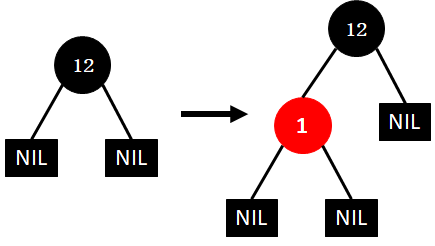
说明：插入的节点若不是根节点，则将其设置为红色

（3）插入9

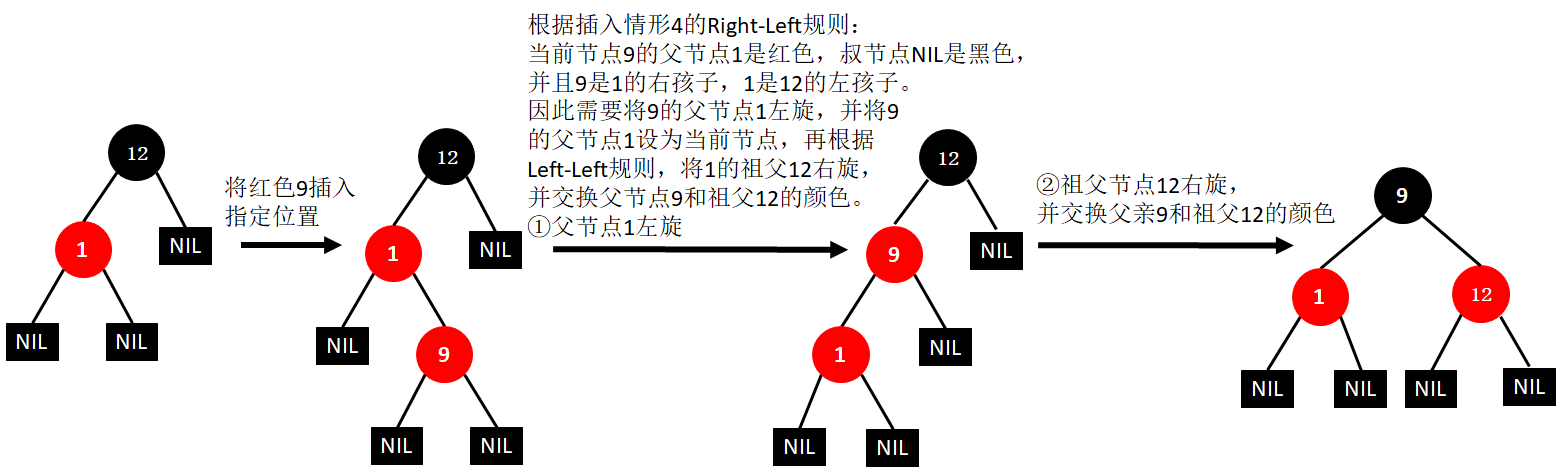
（4）插入2

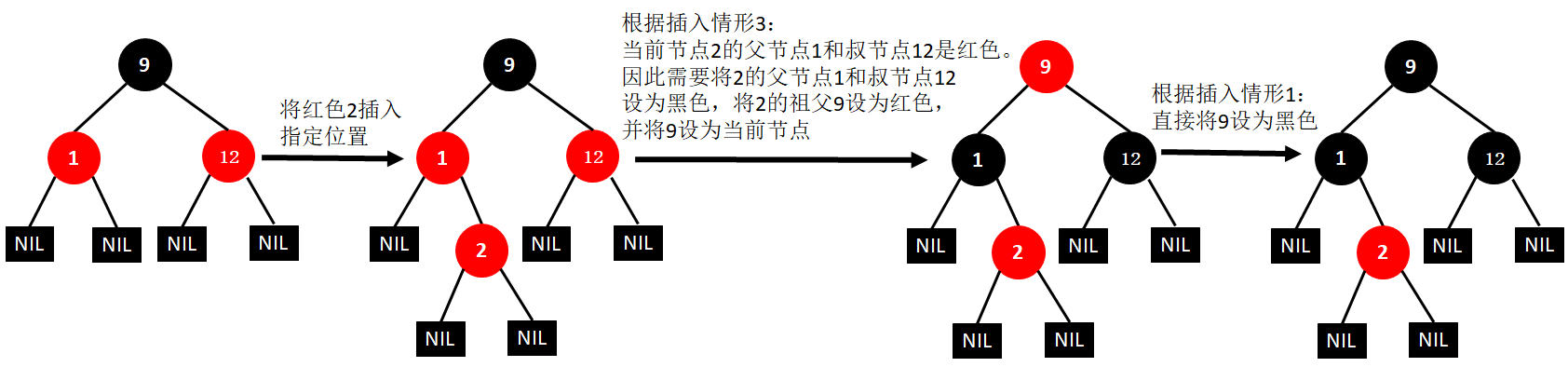
（5）插入0

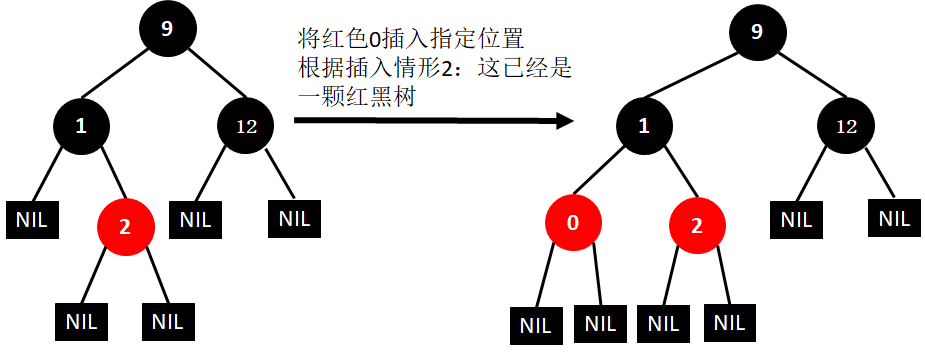
（6）插入11

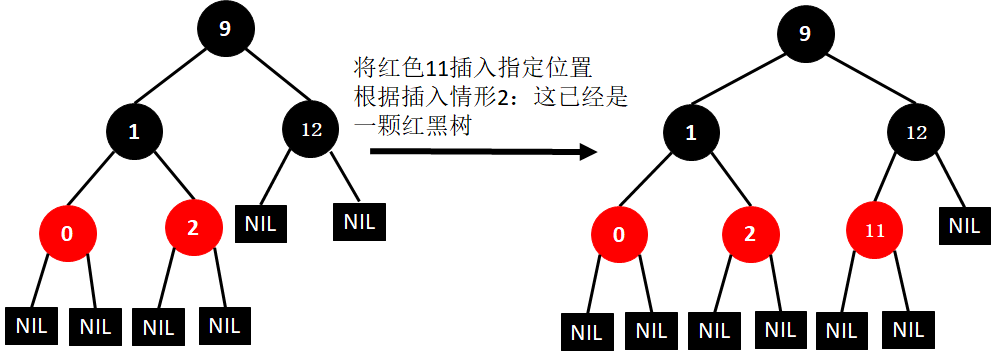
（7）插入7

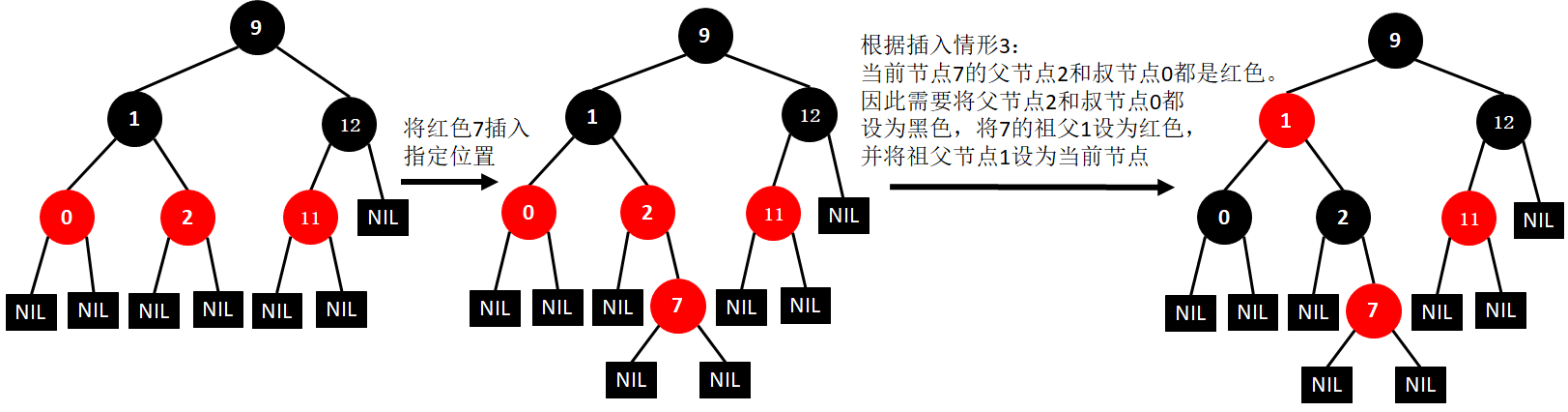
（8）插入19

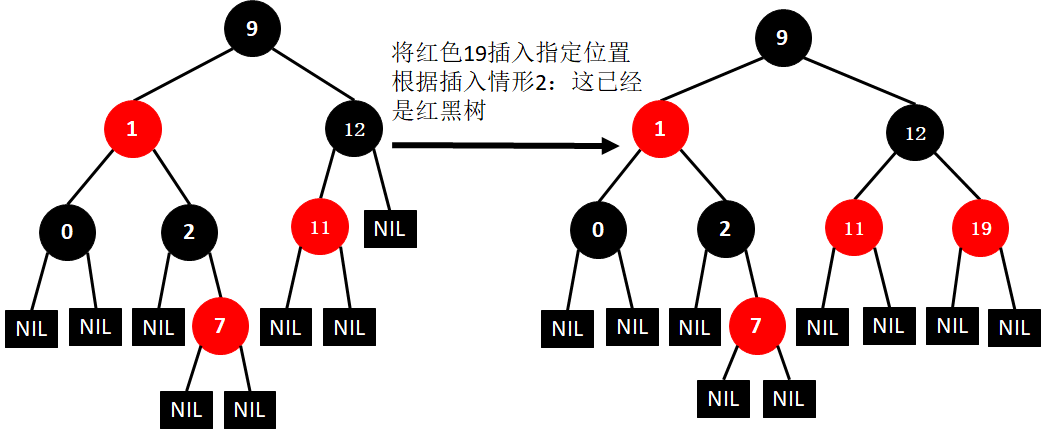
（9）插入4

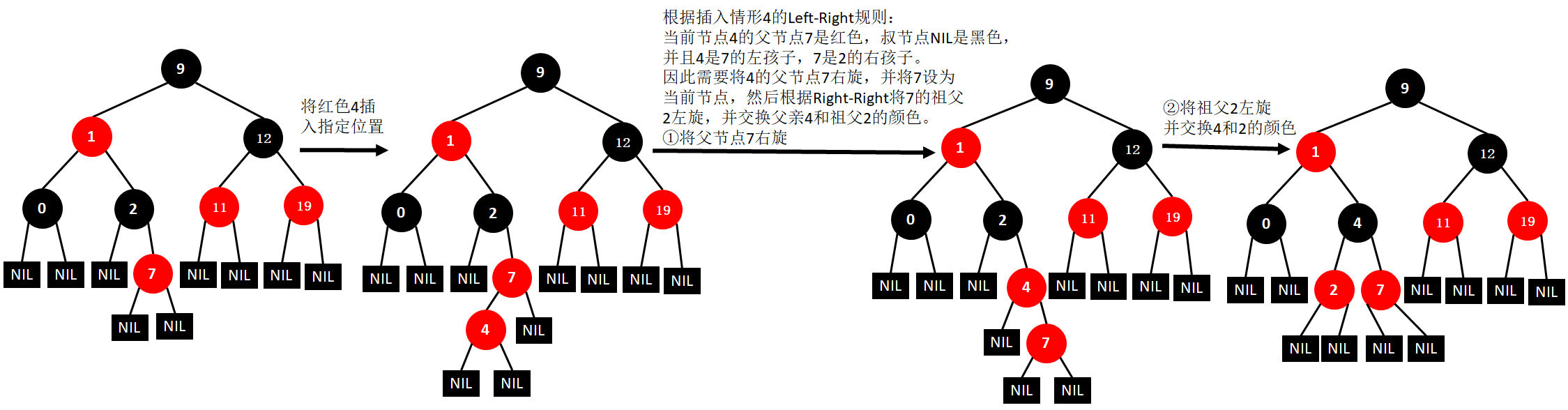
（10）插入15

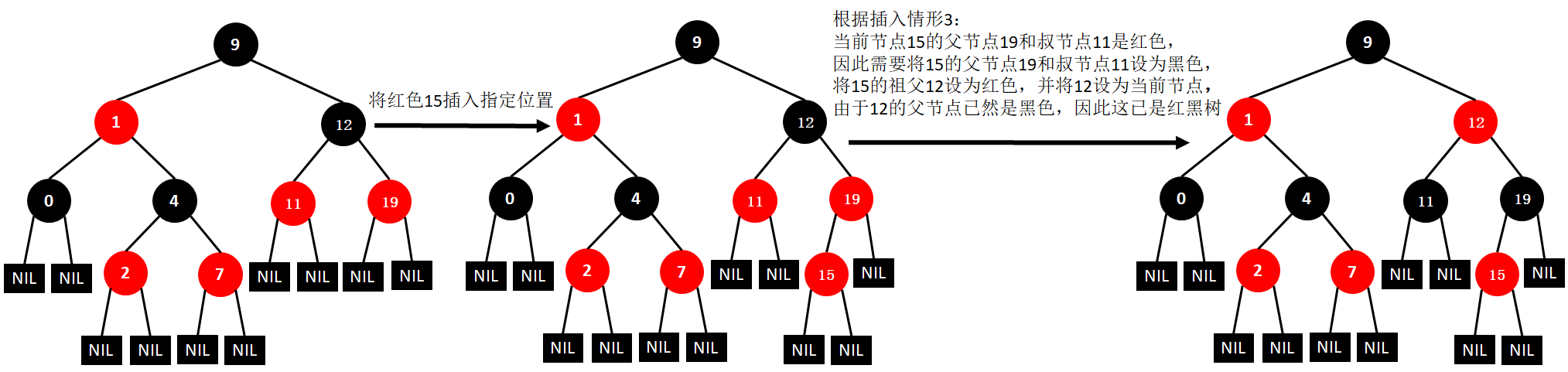
（11）插入18

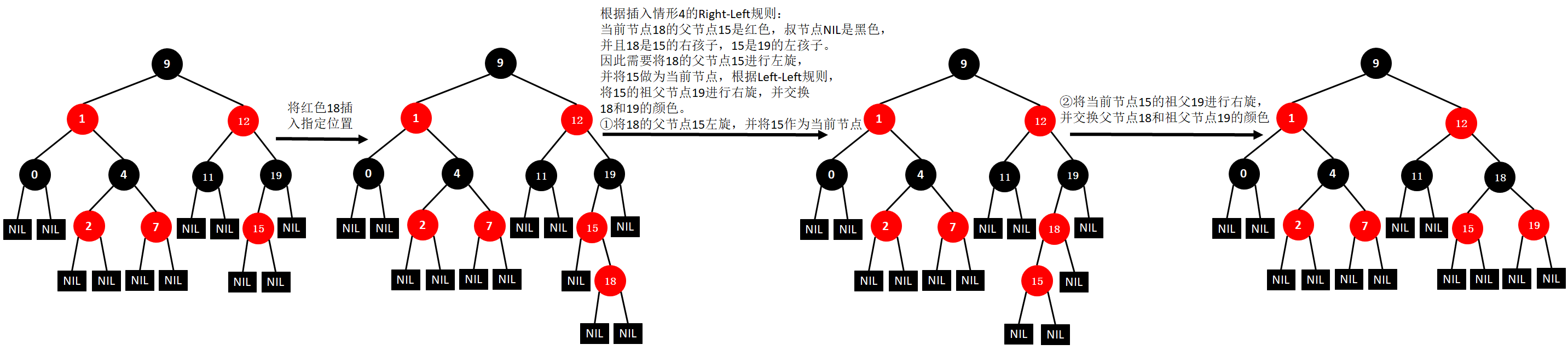
（12）插入5

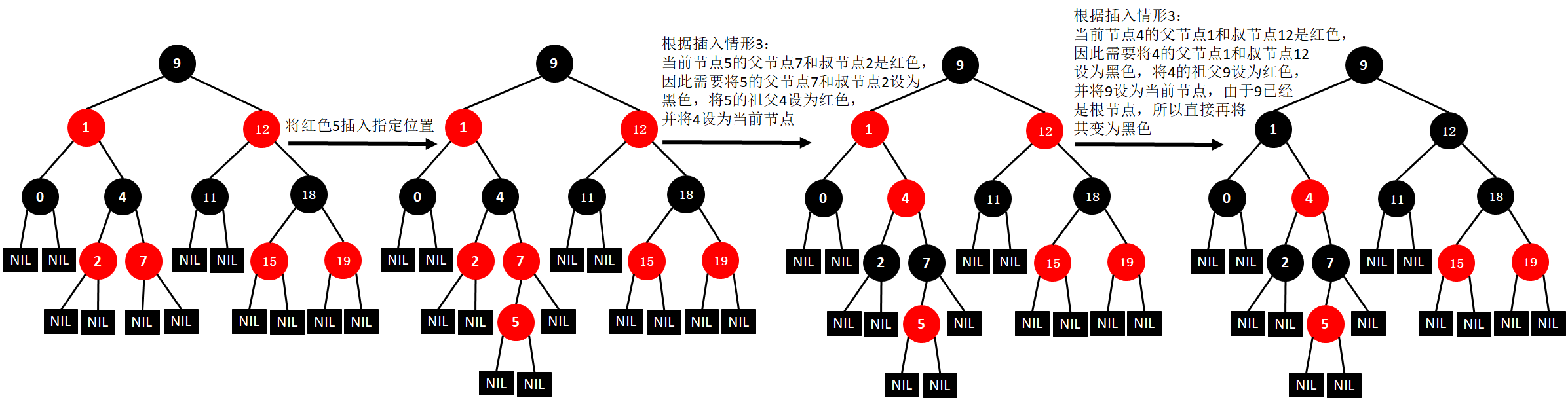
（13）插入14

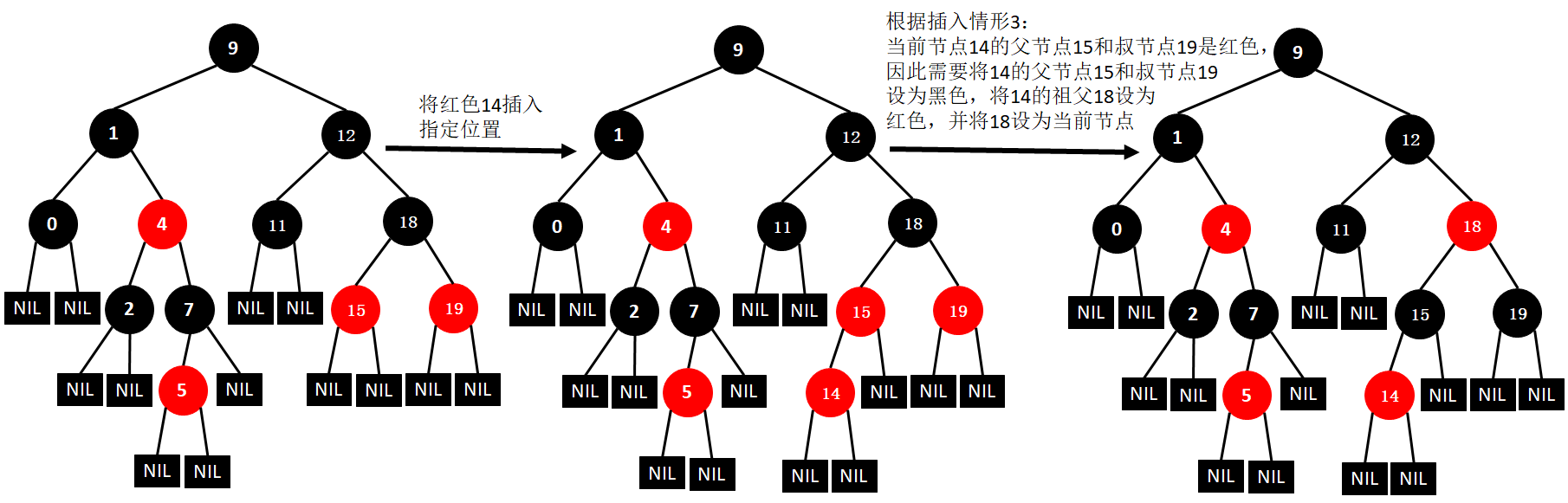
（14）插入13

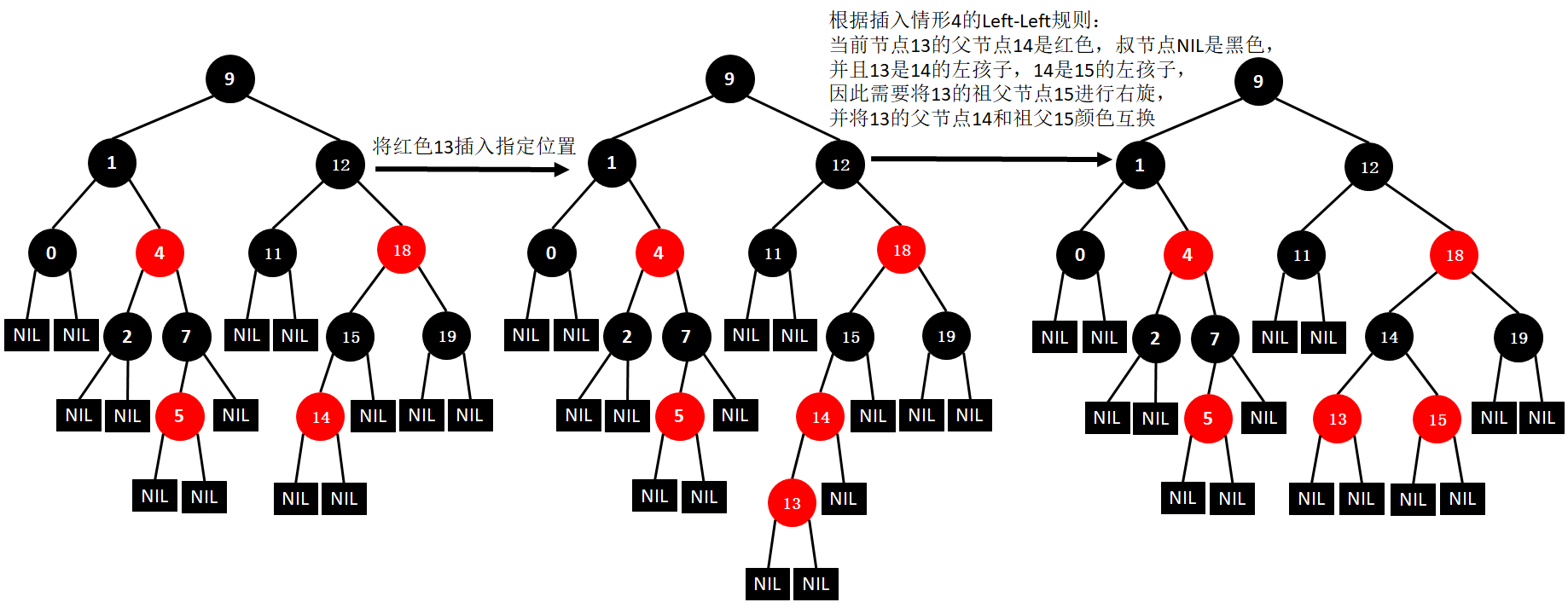
（15）插入10

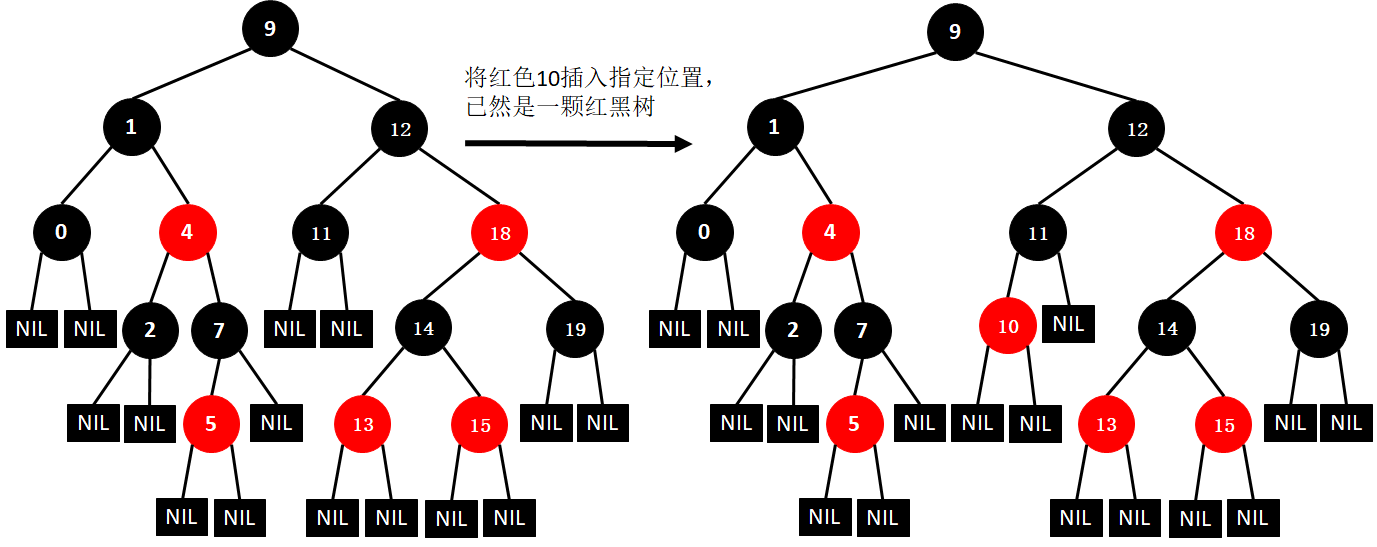
（16）插入16

（17）插入6

（18）插入3

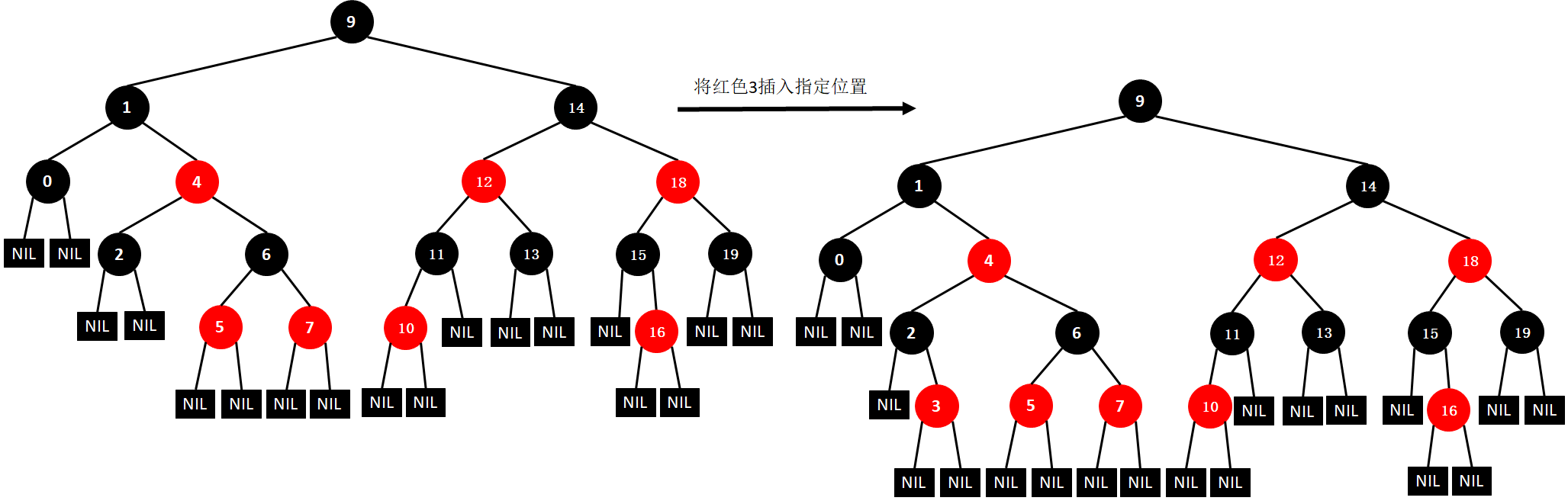
（19）插入8

（20）插入17

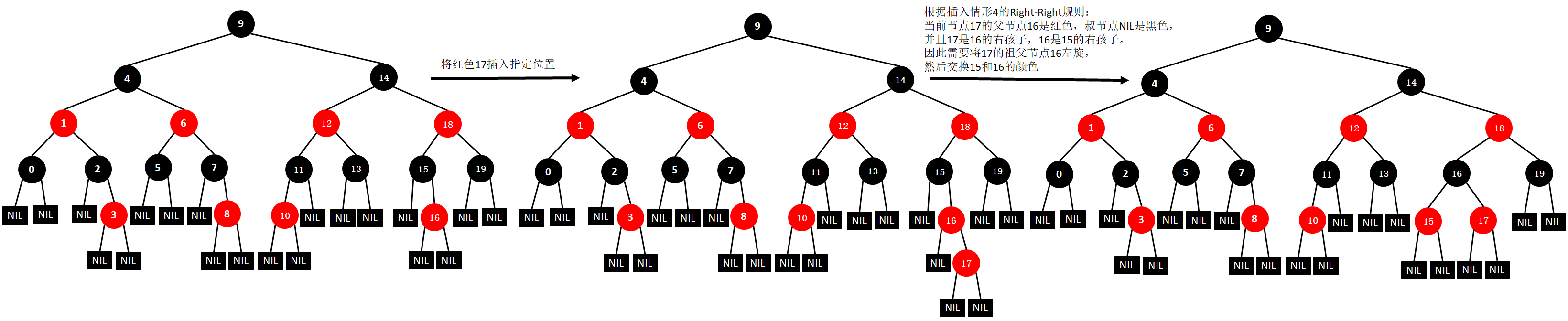
插入的过程讲解完毕。

五、基本操作——删除

1、红黑树删除的情形

一、从树中删除节点X（以寻找后继节点的方式进行删除）

情况①：如果X没有孩子，且如果X是红色，直接删除X；如果X是黑色，则以X为当前节点进行旋转调色，最后删掉X

情况②：如果X只有一个孩子C，交换X和C的数值，再对新X进行删除。根据红黑树特性，此时X不可能为红色，因为红色节点要么没有孩子，要么有两个黑孩子。此时以新X为当前节点进行情况①的判断

情况③：如果X有两个孩子，则从后继中找到最小节点D，交换X和D的数值，再对新X进行删除。此时以新X为当前节点进行情况①或②的判断

二、旋转调色（N=旋转调色的当前节点[等于情况①中的X]，P=N的父亲，W=N的兄弟，Nf=N的远侄子，Nn=N的近侄子）

情况1：N是根或者N是红色，则：直接将N设为黑色

情况2：N不是根且N是黑色，且W为红色，则：将W设为黑色，P设为红色，对P进行旋转(N为P的左子时进行左旋，N为P的右子时进行右旋)，将情况转化为情况1、2、3、4、5

情况3：N不是根且N是黑色，且W为黑色，且W的左右子均为黑色，则：将W设为红色，将P设为当前节点进行旋转调色，将情况转化为情况1、2、3、4、5

情况4：N不是根且N是黑色，且W为黑色，且Nf为黑色，Nn为红色，则：交换W与Nn的颜色，并对W进行旋转(N为P的左子进行右旋，N为P的右子进行左旋)，旋转后N的新兄弟W有一个红色WR，则转换为情况5

情况5：N不是根且N是黑色，且W为黑色，且Nf为红色，Nn为黑色，则：将W设为P的颜色，P和Nf设为黑色，并对P进行旋转(N为P的左子进行左旋，N为P的右子进行右旋)，N设为根

2、插入图例

通过删除12   1   9   2   0   11   7   19   4   15   18   5   14   13   10   16   6   3   8   17完成上述所有情形的展示。

（1）删除12

（2）删除1

（3）删除9

（4）删除2

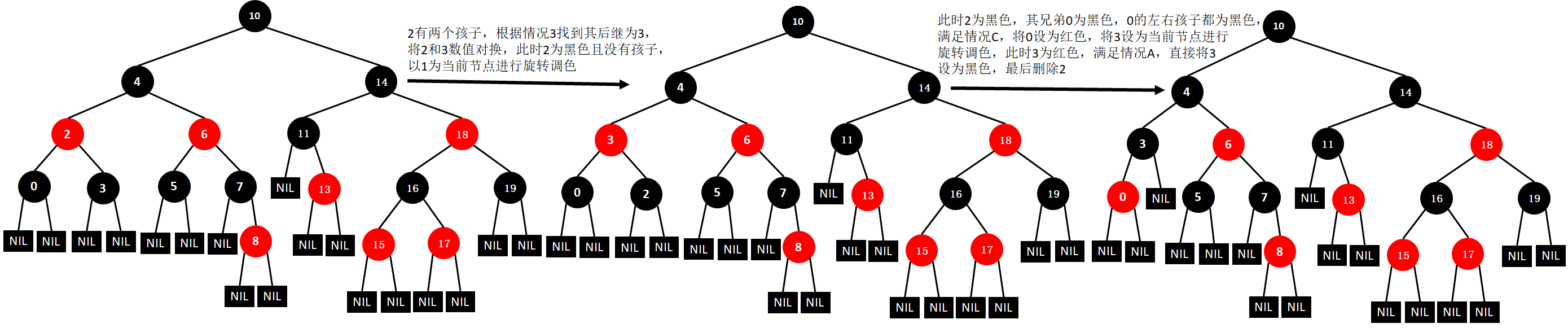
（5）删除0

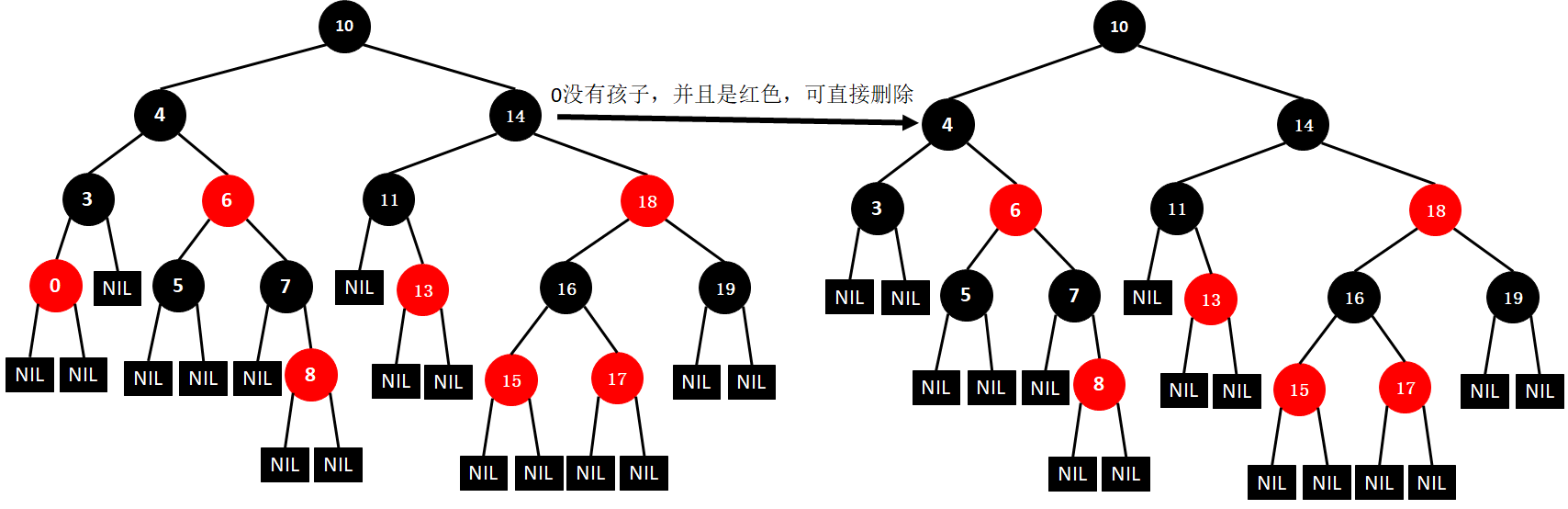
（6）删除11

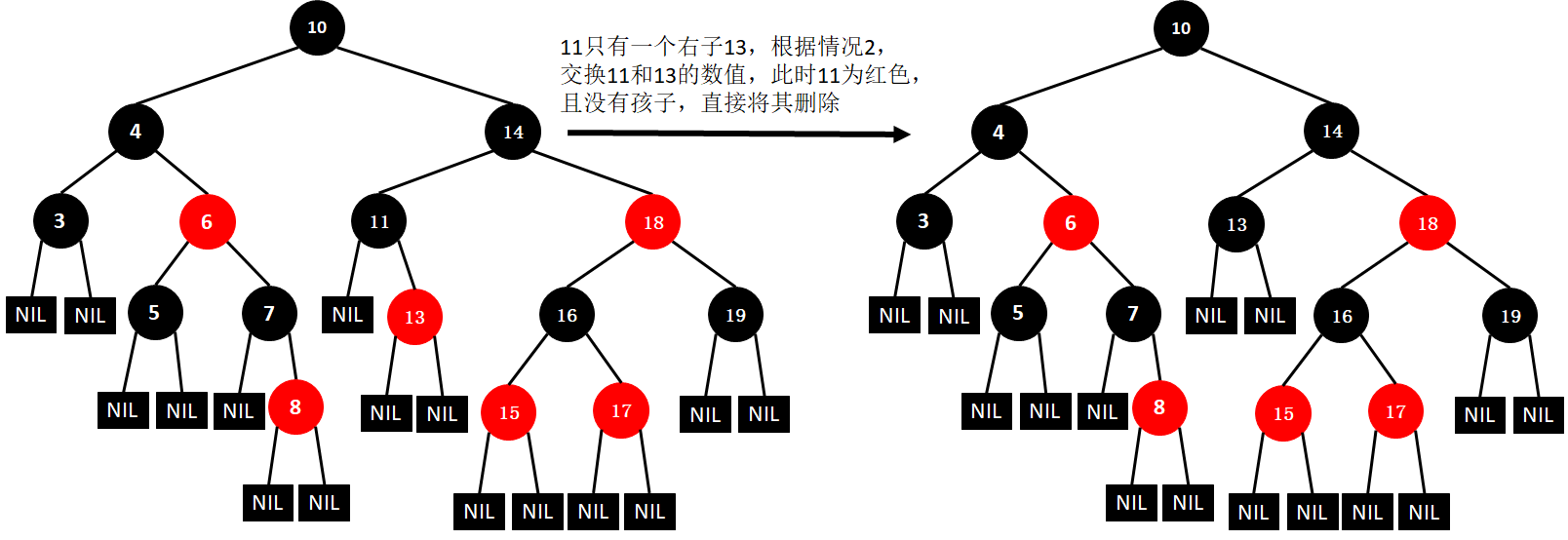
（7）删除7

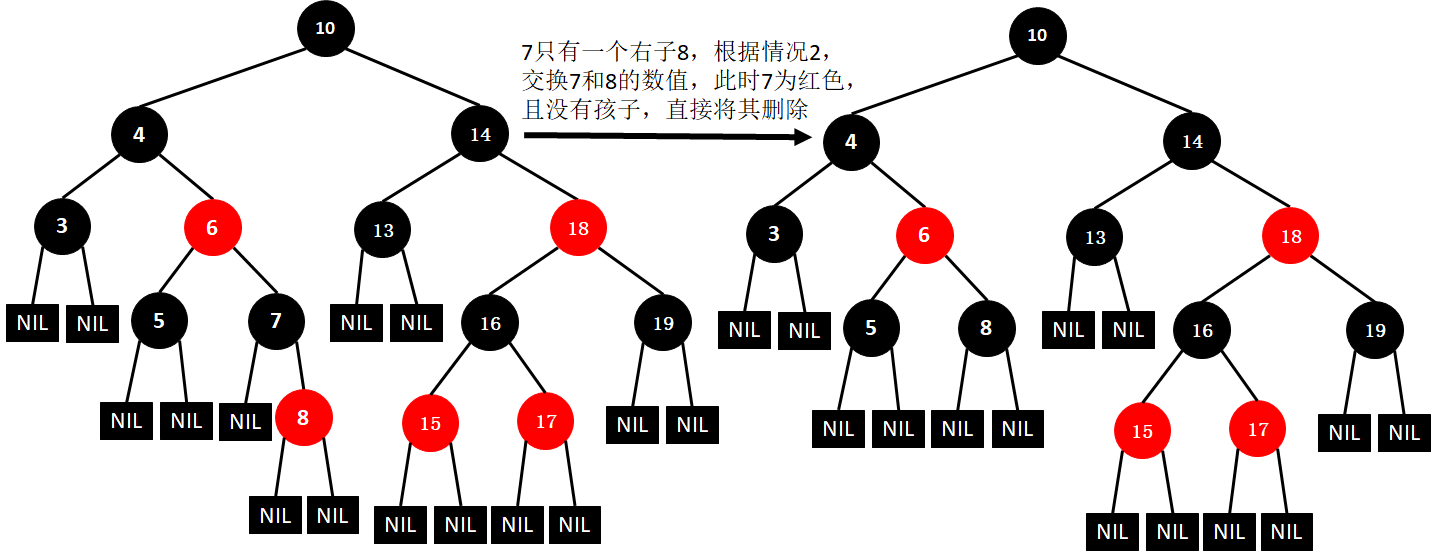
（8）删除19

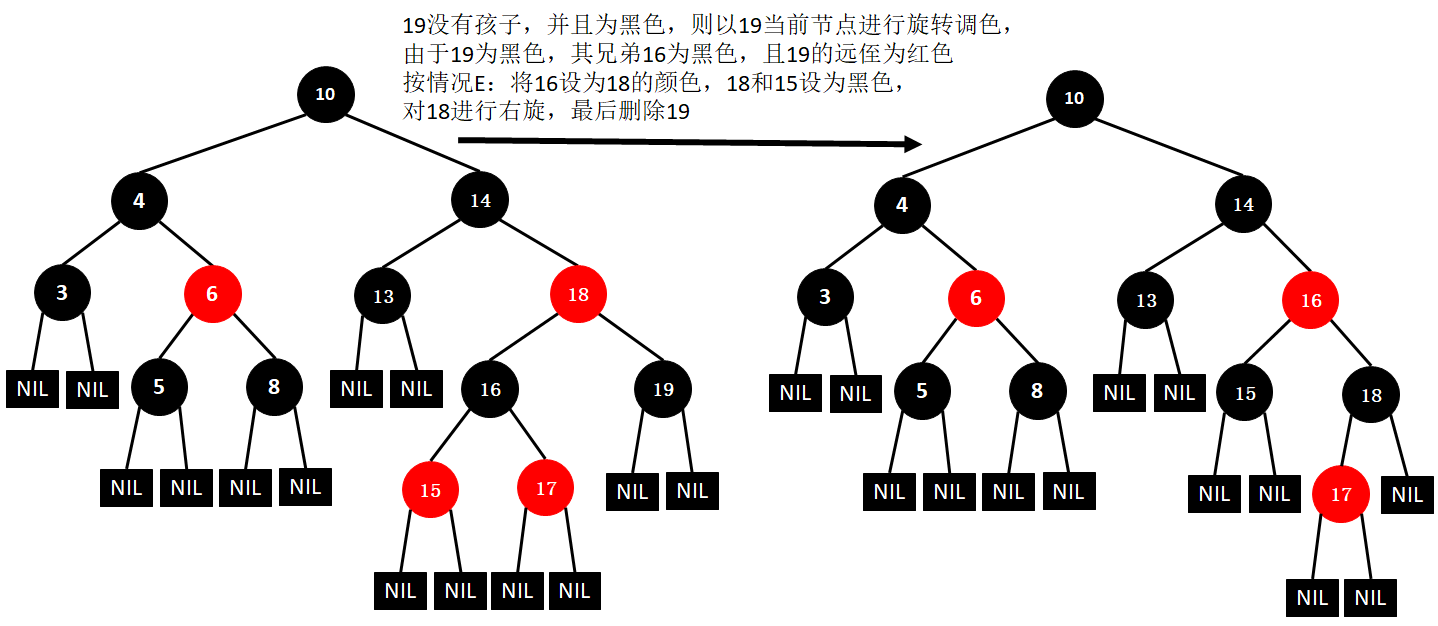
（9）删除4

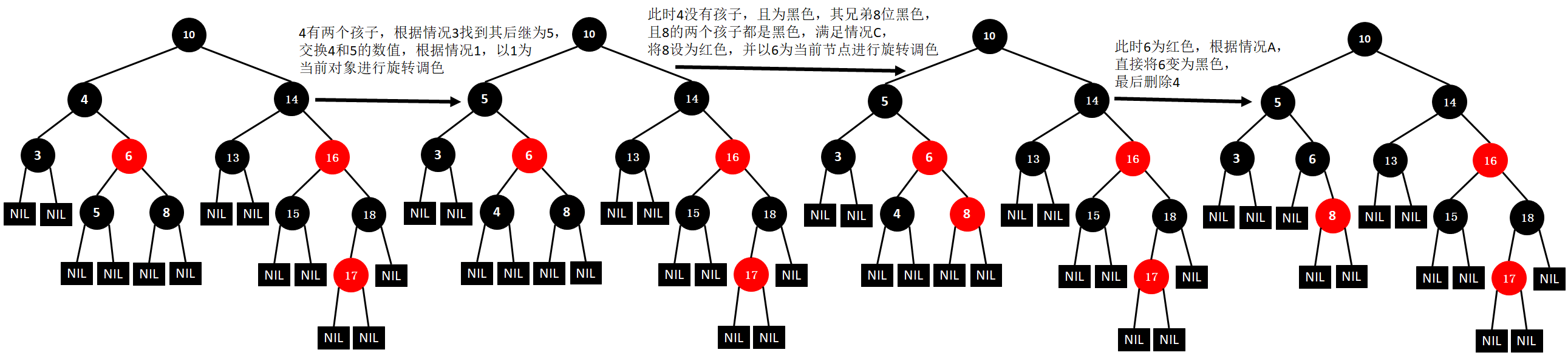
（10）删除15

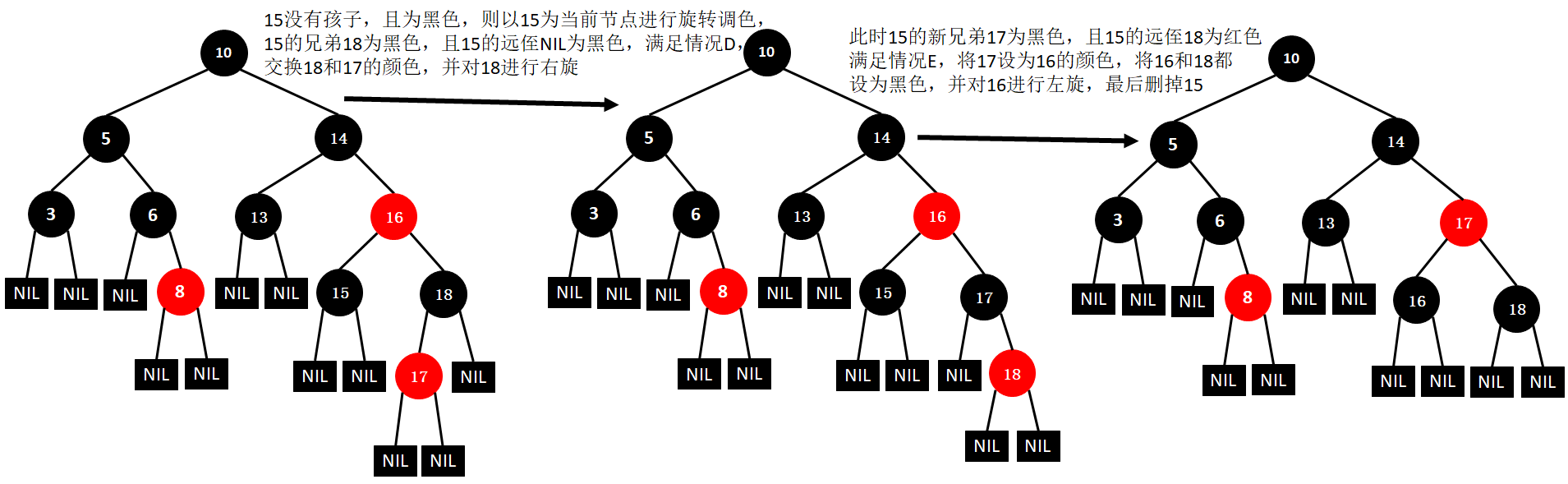
（11）删除18

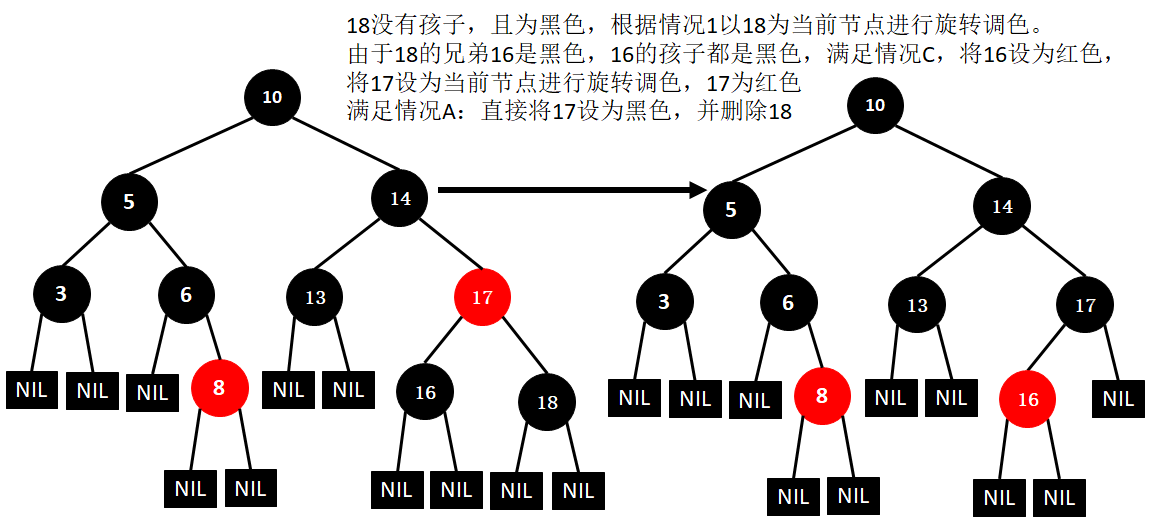
（12）删除5

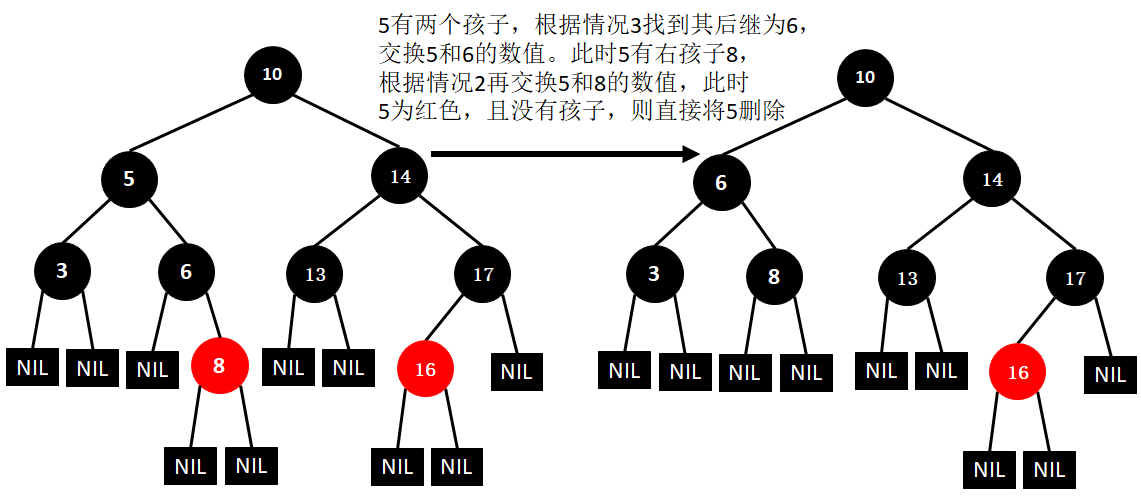
（13）删除14

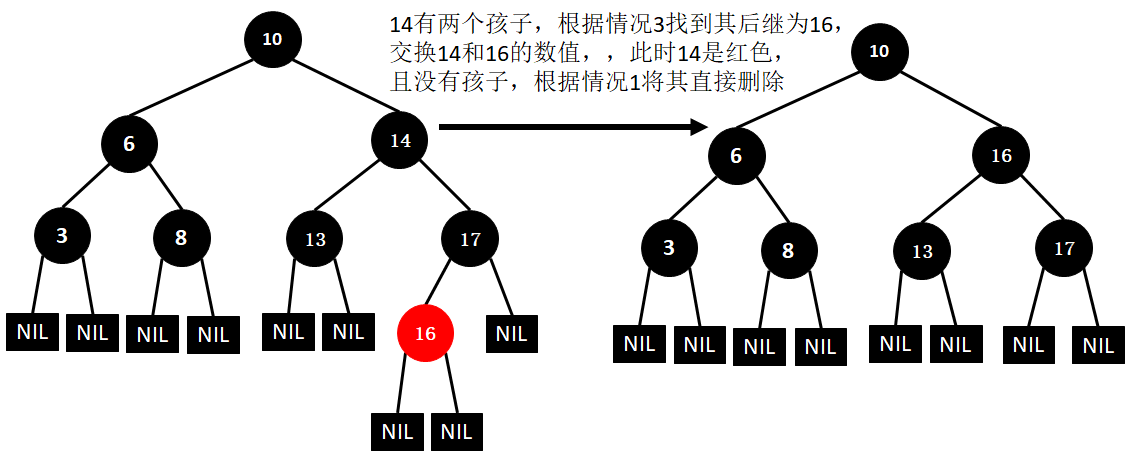
（14）删除13

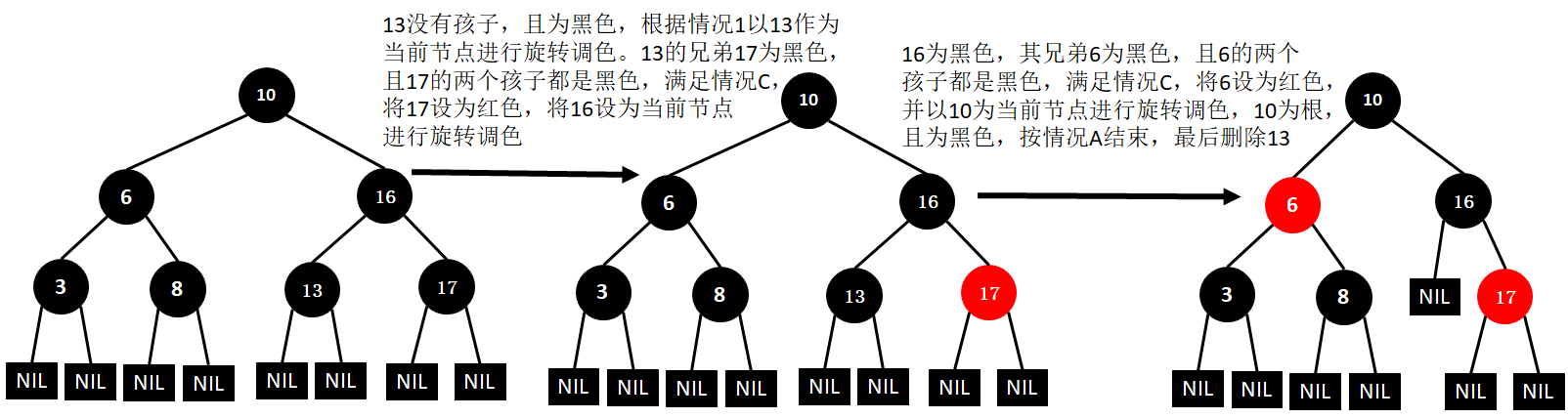
（15）删除10

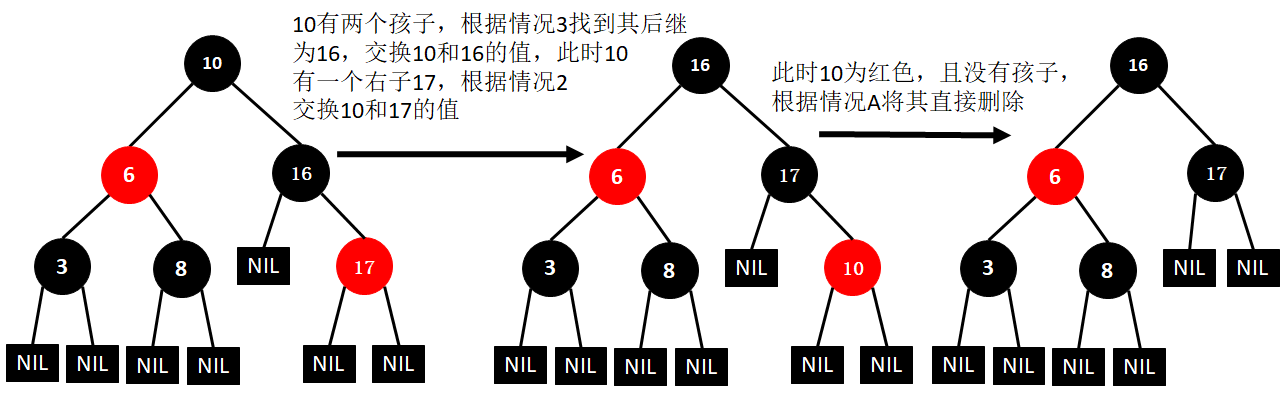
（16）删除16

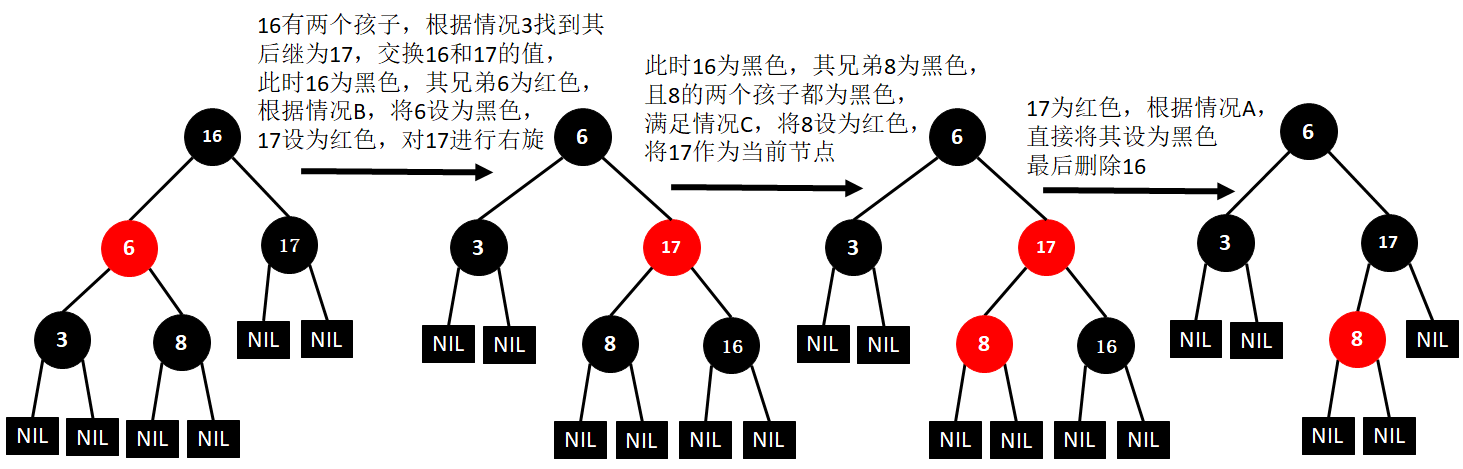
（17）删除6

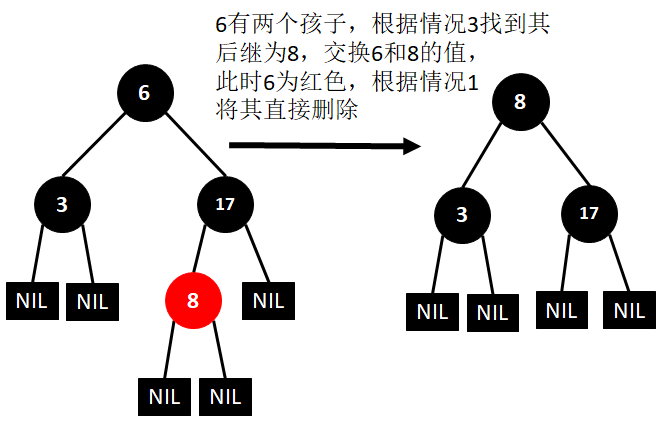
（18）删除3

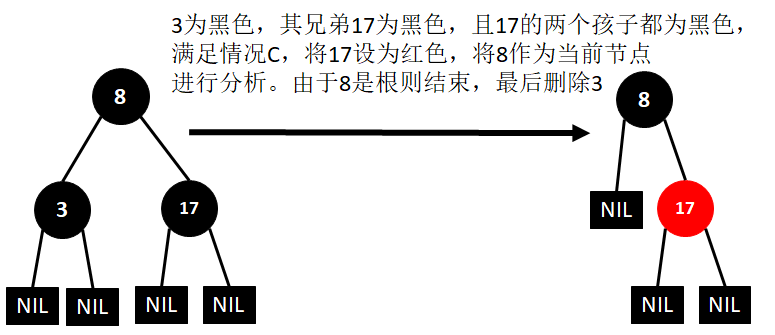
（19）删除8

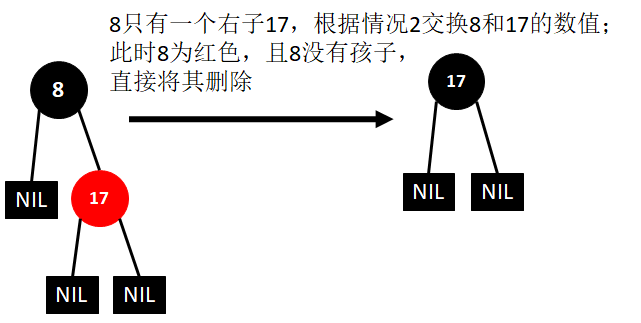
（20）删除20

删除完毕！

参考：红黑树原理以及插入、删除算法 附图例说明