[SWPU2019]EasiestRe-cnblog
[SWPU2019]EasiestRe 双进程保护,特殊的内存自修改,windows异常处理机制
分析程序代码

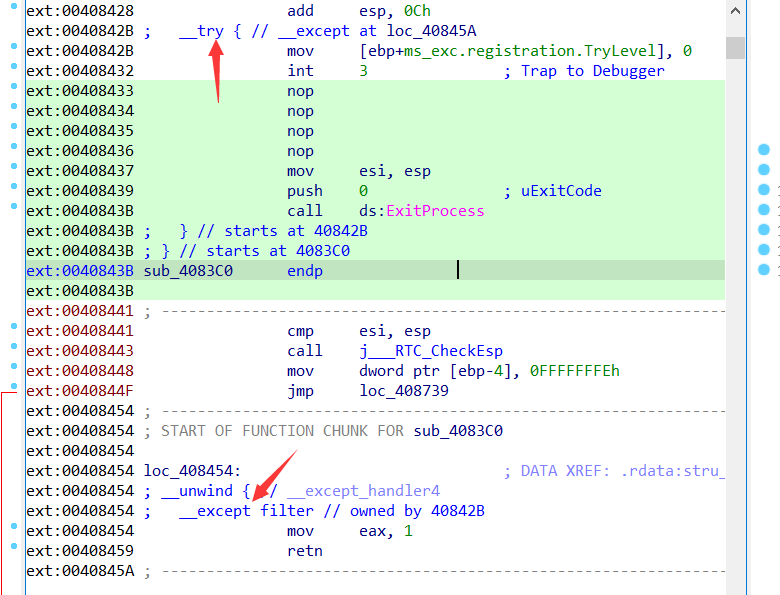
当int 3+nop长度为5时,debugger传回了DBG_EXCEPTION_NOT_HANDLED(0x80010001)信号,告知程序int 3断点导致的错误没有被处理,因此通过c程序的try,except机制跳转到loc_40842B进行处理,回避了ExitProcess的执行。
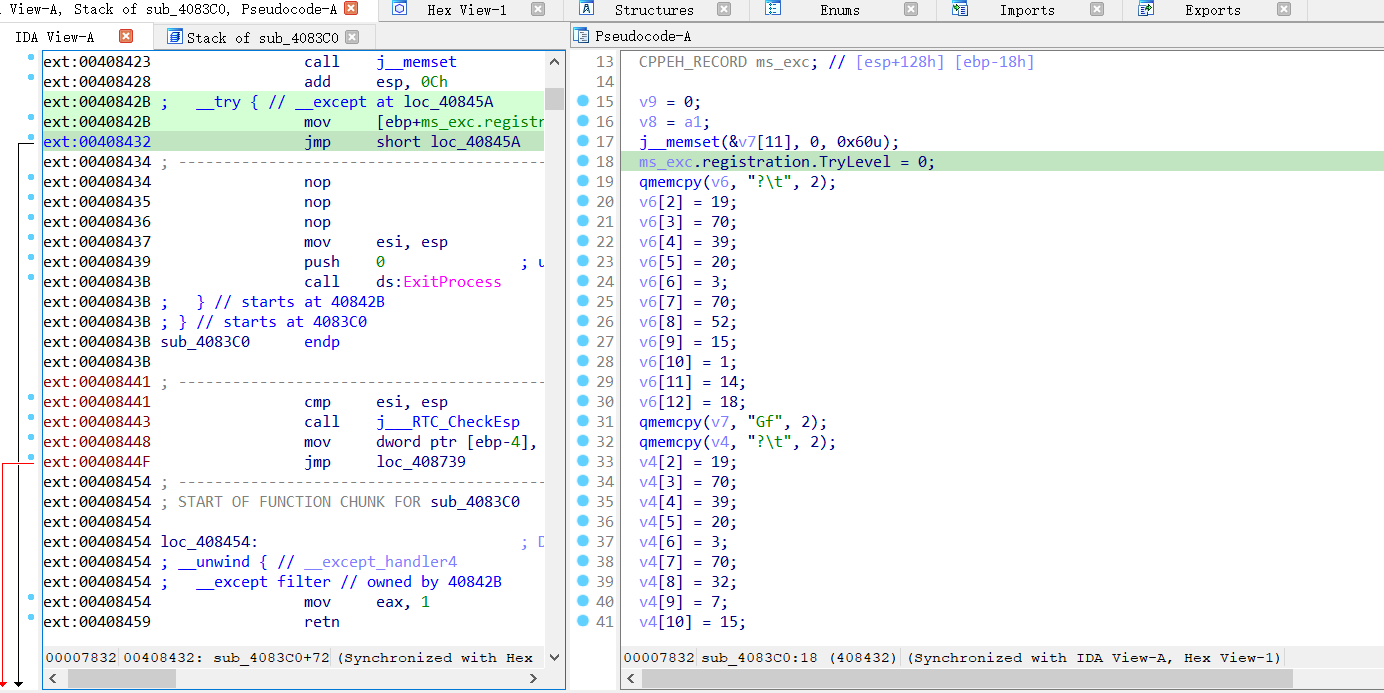
为代码手动添加jmp,后续伪代码被分析出来。
接下来只要对encrypt过程进行逆向,由代码可知是一个Merkle-Hellman背包加密 - CTF Wiki (ctf-wiki.org)](https://ctf-wiki.org/crypto/asymmetric/knapsack/knapsack/)
私钥为[2,3,7,0xE,0x1E,0x39,0x78,0xFB]

关于背包加密的实现原理:
背包密码体制原理大白话讲解及Python实现-阿里云开发者社区 (aliyun.com)
背包加密 - CTF Wiki (ctf-wiki.org)
概念:
超递增集:每一个整数都大于它前面整数之和的集合,例如常见的1、2、4、8、16、32
陷门:可理解为乘数w
设vi为明文,w为乘数,m为模数,ai为私钥,bi为公钥,w-1为逆元 则:
逆元满足w-1*w mod m =1
可知 w-1 * w = 1 + k * m
满足 bi = w*ai mod m
可知 w-1* bi * vi mod m = (1+k*m) * ai * vi mod m = (ai * vi + m * k * ai * vi ) mod m = ai * vi mod m

因此可理解背包加密的原理,并通过加密信息得到原信息,编写代码
v4 = [2, 3, 7, 0xE, 0x1E, 0x39, 0x78, 0xFB]
data = [0x3D1, 0x2F0, 0x52, 0x475, 0x1D2, 0x2F0, 0x224, 0x51C, 0x4E6, 0x29F, 0x2EE, 0x39B, 0x3F9, 0x32B, 0x2F2, 0x5B5,
0x24C, 0x45A, 0x34C, 0x56D, 0x0A, 0x4E6, 0x476, 0x2D9]
# for i in range(8):
# v4[i] = 41 * v4[i] % 0x1EB
x = 12
v4.reverse()
arr = []
for i in range(24):
dec = data[i] * x % 0x1EB
# print(dec)
ascii_char = 0
for j in range(8):
if dec >= v4[j] :
ascii_char += 2 ** j
dec -= v4[j]
arr.append(ascii_char)
f = [4660]
f.extend(data)
flag = "".join(chr((arr[i]^f[i])%256) for i in range(24))
print(flag)
swpuctf{y0u_@re_s0_coo1}



