Taylor series Explicit Euler Implicit Euler
1 Taylor series
\[\begin{gathered}\sum_{n=0}^{\infty}\frac{f^{(n)}\left(a\right)}{n!}\left(x-a\right)^{n}\\f\left(a\right)+\frac{f^{\prime}\left(a\right)}{1!}(x-a)+\frac{f^{\prime\prime}\left(a\right)}{2!}(x-a)^{2}+\frac{f^{\prime\prime\prime}\left(a\right)}{3!}(x-a)^{3}+\ldots\end{gathered}
\]
\[y(t+\Delta t)=y(t)+\Delta ty'(t)+\frac{1}{2}\Delta t^{2}y''(t)+\frac{1}{3!}\Delta t^{3}y'''(t)+...
\]
2 Explicit Euler
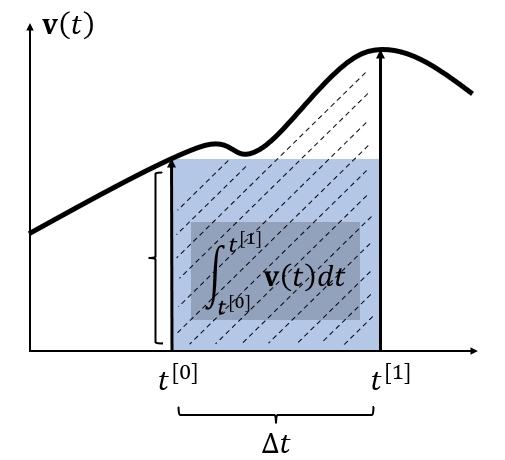
\[\Delta{t} = t_1 - t_0
\]
\[\begin{aligned}
\int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt& =\Delta t\mathbf{v}\big(t^{[0]}\big)+\frac{\Delta t^{2}}{2}\mathbf{v}'\big(t^{[0]}\big)+\cdots \\
&=\Delta t\left.\mathbf{v}(t^{[0]}) + O(\Delta t^2)\right.
\end{aligned}
\]
\[\mathbf{x}\big(t^{[1]}\big) - \mathbf{x}\big(t^{[0]}\big) = [\text{Taylor at } \mathbf{x}\big(t^{[1]}\big) \text{ based on } \mathbf{x}\big(t^{[0]}\big)] - \mathbf{x}\big(t^{[0]}\big)
\]
3 Implicit Euler
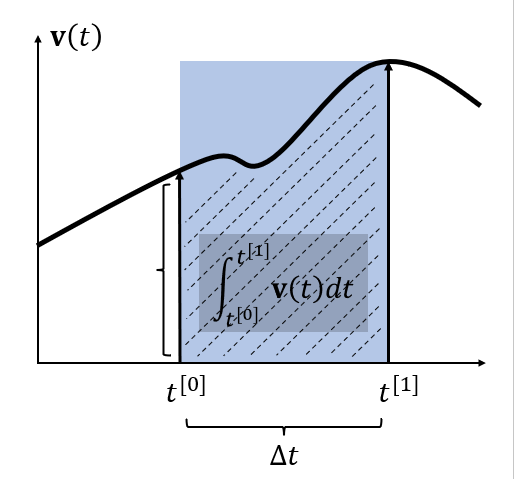
\[\Delta{t} = t_1 - t_0
\]
\[\begin{aligned}
\int_{t^{[0]}}^{t^{[1]}}\mathbf{v}(t)dt& =\Delta t\mathbf{v}\big(t^{[1]}\big)-\frac{\Delta t^{2}}{2}\mathbf{v}'\big(t^{[1]}\big)+\cdots \\
&=\Delta t\left.\mathbf{v}(t^{[1]})+O(\Delta t^2)\right.
\end{aligned}
\]
\[\mathbf{x}\big(t^{[1]}\big) - \mathbf{x}\big(t^{[0]}\big) = \mathbf{x}\big(t^{[1]}\big) - [\text{Taylor at } \mathbf{x}\big(t^{[0]}\big) \text{ based on } \mathbf{x}\big(t^{[1]}\big)]
\]
X ref
如果我的工作对您有帮助，您想回馈一些东西，你可以考虑通过分享这篇文章来支持我。我非常感谢您的支持，真的。谢谢！
作者：Dba_sys (Jarmony)
转载以及引用请注明原文链接：https://www.cnblogs.com/asmurmur/p/17924955.html
本博客所有文章除特别声明外，均采用CC 署名-非商业使用-相同方式共享 许可协议。
