Machine Learning Week_8 K-means And PCA

目录

• 1 K-means
  • 1.1 Unsupervised Learning:Introduction
  • 1.2 K-Means Algorithm
    • 1.2.1 k-means algorithm
  • 1.3 Optimization Objective
    • 1.3.1 K-means optimization objective
  • 1.4 Random Initialization
    • 1.4.1 Random initialzation
    • 1.4.2 Code
  • 1.5 Choosing the Number of Clusters
  • 1.6 K-means with Image Compression
• 2 PCA
  • 2.1 Motivation I: Data Compression
  • 2.2 Motivation II: Visualization
  • 2.3 Principal Component Analysis Problem Formulation
  • 2.4 Principal Component Analysis Algorithm
    • 2.4.1 Feature scaling/mean nomalization
    • 2.4.2 PCA
  • 2.5 Reconstruction from Compressed Representation
  • 2.6 Choosing the Number of Principal Components
  • 2.7 Advice for Applying PCA
    • 2.2.1 Supervised learning speedup
    • 2.7.2 PCA is sometimes used where it shouldn’t be.

1 K-means

1.1 Unsupervised Learning:Introduction

In this video, I'd like to start to talk about clustering.

This will be exciting, because this is our first unsupervised learning algorithm, where we learn from unlabeled data instead from labelled data.

So, what is unsupervised learning? I briefly talked about unsupervised learning at the beginning of the class but it's useful to contrast it with supervised learning. So, here's a typical supervised learning problem where we're given a labeled training set and the goal is to find the decision boundary that separates the positive label examples and the negative label examples. So, the supervised learning problem in this case is given a set of labels to fit a hypothesis to it.

In contrast, in the unsupervised learning problem we're given data that does not have any labels associated with it. So, we're given data that looks like this. Here's a set of points add in no labels, and so, our training set is written just x1, x2, and so on up to xm and we don't get any labels y. And that's why the points plotted up on the figure don't have any labels with them. So, in unsupervised learning what we do is we give this sort of unlabeled training set to an algorithm and we just ask the algorithm find some structure in the data for us. Given this data set one type of structure we might have an algorithm find is that it looks like this data set has points grouped into two separate clusters.

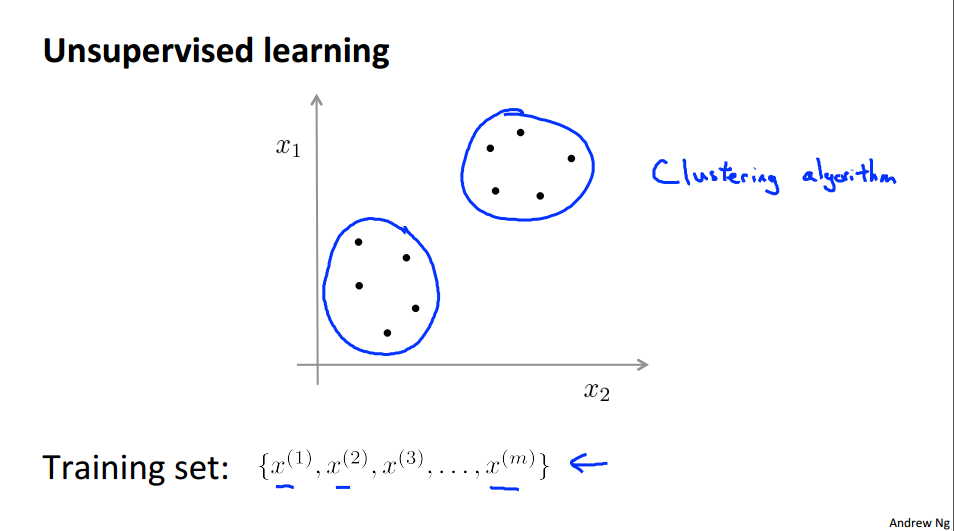
So an algorithm that finds clusters like the ones I've just circled is called a clustering algorithm. And this would be our first type of unsupervised learning, although there will be other types of unsupervised learning algorithms that we'll talk about later that finds other types of structure or other types of patterns in the data other than clusters. We'll talk about this after we've talked about clustering.

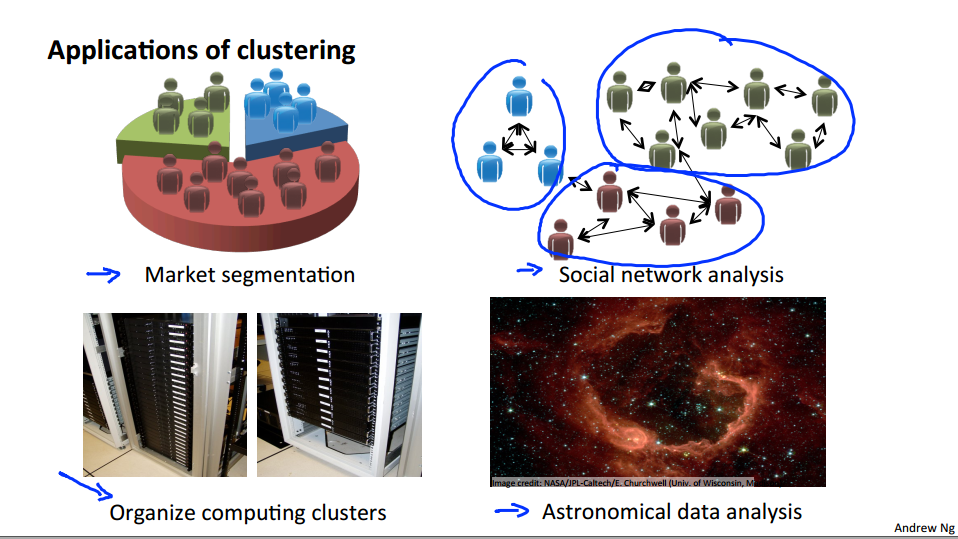
So, what is clustering good for? Early in this class I already mentioned a few applications.

One is market segmentation where you may have a database of customers and want to group them into different marker segments so you can sell to them separately or serve your different market segments better. Social network analysis. There are actually groups have done this things like looking at a group of people's social networks. So, things like Facebook, Google+, or maybe information about who other people that you email the most frequently and who are the people that they email the most frequently and to find coherence in groups of people. So, this would be another maybe clustering algorithm where you know want to find who are the coherent groups of friends in the social network? Here's something that one of my friends actually worked on which is, use clustering to organize computer clusters or to organize data centers better. Because if you know which computers in the data center in the cluster tend to work together, you can use that to reorganize your resources and how you layout the network and how you design your data center communications. And lastly, something that actually another friend worked on using clustering algorithms to understand galaxy formation and using that to understand astronomical data.

So, that's clustering which is our first example of an unsupervised learning algorithm. In the next video we'll start to talk about a specific clustering algorithm.

1.2 K-Means Algorithm

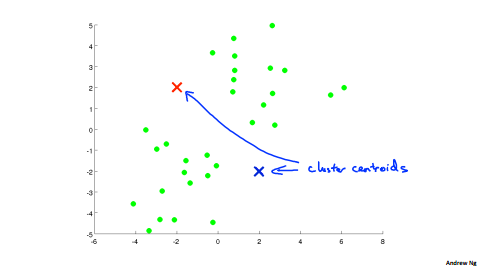
In the clustering problem we are given an unlabeled data set and we would like to have an algorithm automatically group the data into coherent subsets or into coherent clusters for us. The K Means algorithm is by far the most popular, by far the most widely used clustering algorithm.

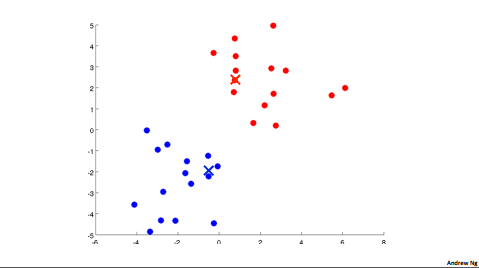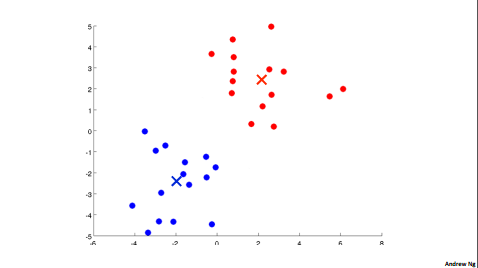1.2.1 k-means algorithm

input

• K (number of clusters)
• Training set \({x^{(1)}, x^{(2)}, ..., x^{(m)}}\)
• \(x^{(i)} \in R^n\) (drop \(x_0=1\) convention)

First step:
　Randomly initialize k cluster centroids \(\mu_1, \mu_2,..., \mu_k\)
　\(\mu_k \in R^n\)

Second step:
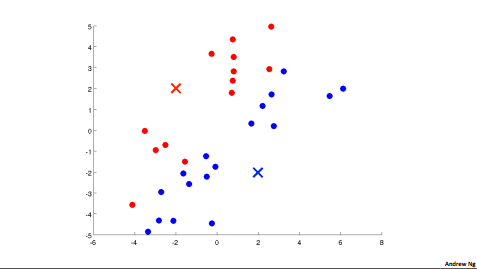
　repeat
　{
　　　//cluster assignment step;
　　　//\(min_k ||x^{(1)}||\)
　　　for i = 1 to m
　　　　\(c^{(i)}\):= Index(from 1 to k) of cluster centroid closest to x^{(i)}

　　　//move centroid step
　　　for k = 1 to k
　　　　// i.e. \(\mu_2 = \frac{1}{4}[x^{(1)} + x^{(2)}+x^{(5)}+x^{(6)}]\)
　　　　\(\mu_k\):= average(mean) of points assigned to clusters

　}

1.3 Optimization Objective

Most of the supervised learning algorithms we've seen, things like linear regression, logistic regression, and so on, all of those algorithms have an optimization objective or some cost function that the algorithm was trying to minimize. It turns out that k-means also has an optimization objective or a cost function that it's trying to minimize. And in this video I'd like to tell you what that optimization objective is.

1.3.1 K-means optimization objective

term
\(c^{(i)}\) = index of cluster (1,2,...,k) to which eample \(x^{(i)}\) is currently assigned
\(\mu_k\) = cluster centroid k
\(\mu_{c^{(i)}}\) = cluster centroid of cluster to which example \(x^{(i)}\) has been assigned

Optimization objective

\[J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_k) = \frac{1}{m}\sum_{i=1}^{m}||x^{(i)}-\mu_{c^{(i)}}||^2 \]

\[min_{c^{(1)},...,c^{(m)},\; \mu_1,...,\mu_k}\;J(...) \]

1.4 Random Initialization

1.4.1 Random initialzation

should have k < m

1. Randomly pick k training examples.
2. Set \(\mu_1 ,...,\mu_k\) equal to these k examples

Depending on the random initialzation, k-means can end up at different solutions (End up local optima)

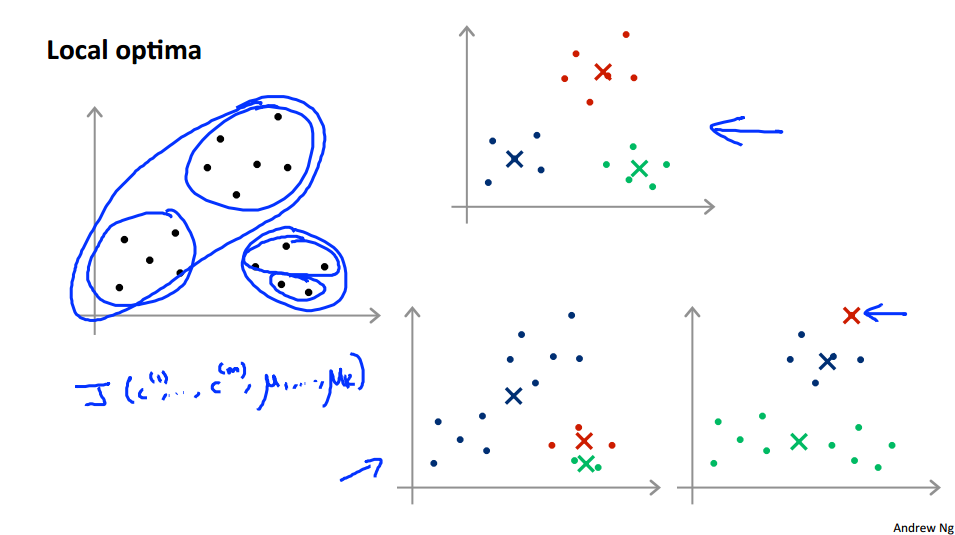
what we can do , is try multiple random initializations, and use that try to make sure we get as good solution.

1.4.2 Code

for i=1 to 100
{
　　Randomly initialize K-means
　　Run K-means. Get \(c^{(1)},...,c^{(m)},\mu_1 ,...,\mu_k\)
　　Compute cost function(distortation)
　　\(J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_k) = \frac{1}{m}\sum_{i=1}^{m}||x^{(i)}-\mu_{c^{(i)}}||^2\)
}
Pick clustering that gave lowest cost J.

事实证明 \(K \in {2,3,4,..,10}\) 小聚类时，多次运行会很有好处，一旦中心数过于多，多次运行也不会有很好的优化效果。

1.5 Choosing the Number of Clusters

In this video I'd like to talk about one last detail of K-means clustering which is how to choose the number of clusters, or how to choose the value of the parameter K. To be honest, there actually isn't a great way of answering this. Doing this automatically and by far the most common way of choosing the number of clusters, is still choosing it manually by looking at visualizations or by looking at the output of the clustering algorithm or something else.

自动选择K，那么要多次挑选不同的K值，画出对应的曲线图，让我们更好的理解。像是第一张图片里的 Elbow，有一个很清晰的拐点。但有时你并不能很好的观察到这个拐点，这就是自动选择的缺点。

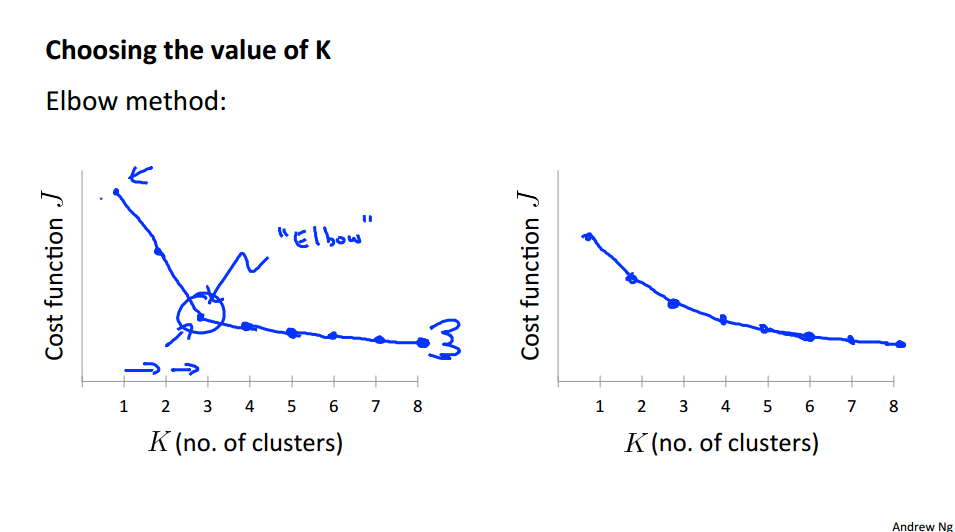
Sometimes, you're running K-means to get clusters to use for some later/downstrem purpose. Evaluate K-means based on a metric for how well it performs for that later purpose.

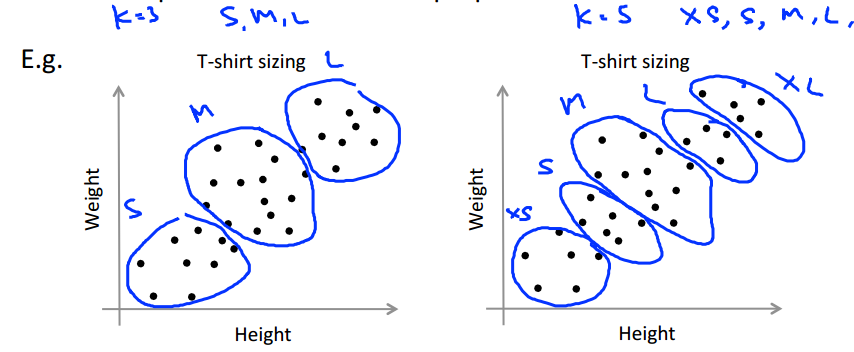
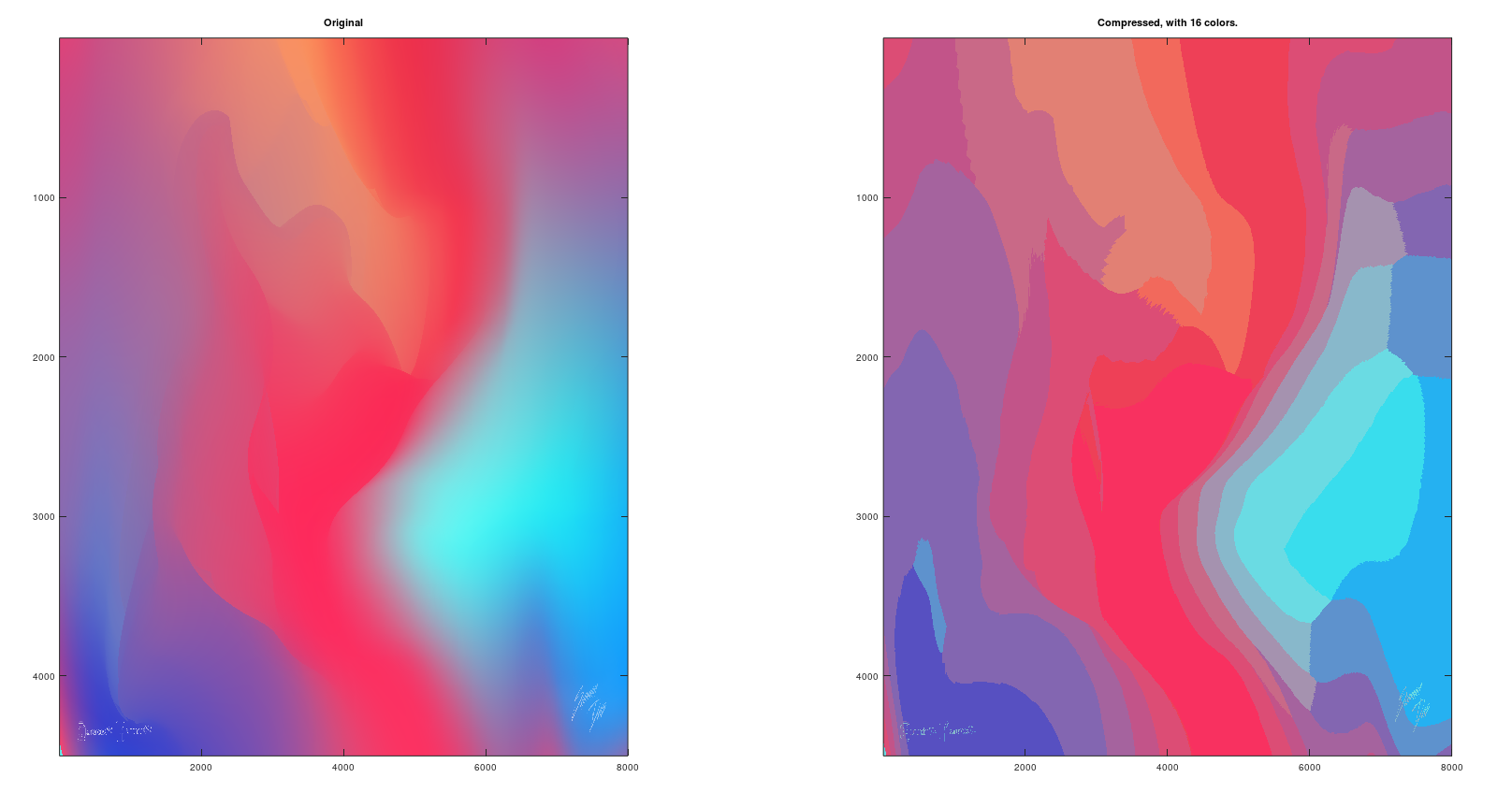
1.6 K-means with Image Compression

2 PCA

2.1 Motivation I: Data Compression

In this video, I'd like to start talking about a second type of unsupervised learning problem called dimensionality reduction.

There are a couple of different reasons why one might want to do dimensionality reduction. One is data compression, and as we'll see later, a few videos later, data compression not only allows us to compress the datapp and have it therefore use up less computer memory or disk space, but it will also allow us to speed up our learning algorithms.

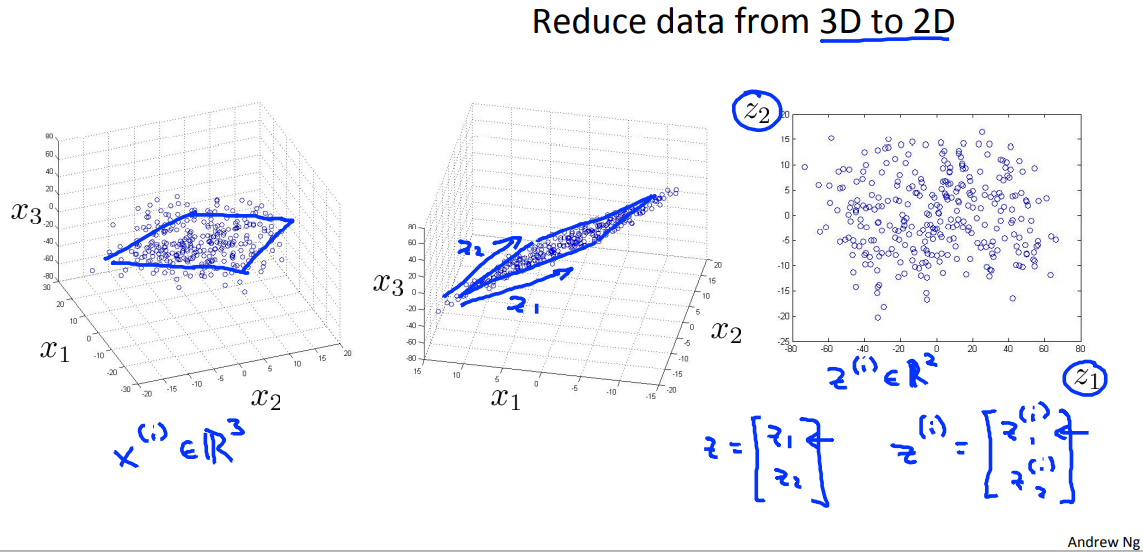
虽然是一个二维的点集(多个二维向量组成的集合)， 但要找到这点集的适合的一条直线(方程 )，就可以通过一个点的位置，也就是是一个标量来确定一个二维的点。(Reduce data from 2D to 1D).

一个3维的点集，只要找到一个适合的平面，就可以通过2维向量点确定原来的3维点的位置。

2.2 Motivation II: Visualization

通常是将数据降到2D或者3D来让我们对于数据有更好的理解。

2.3 Principal Component Analysis Problem Formulation

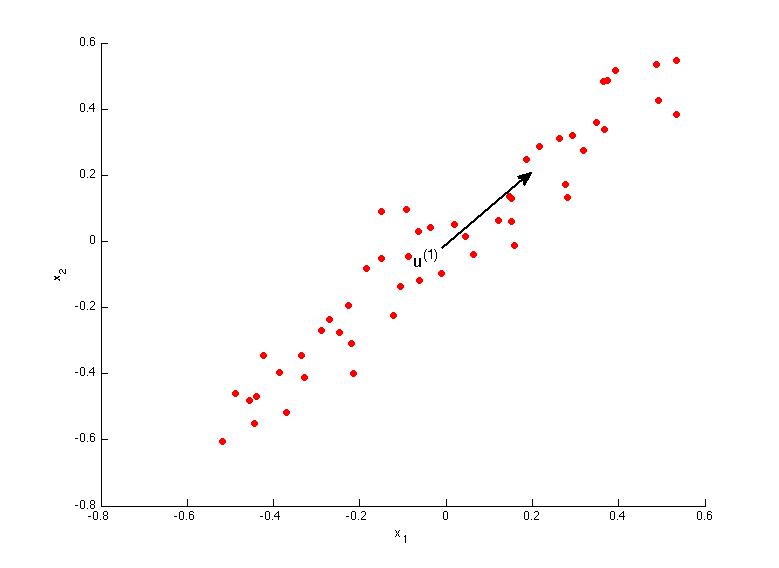
Reudce from 2-dimention to 1-dimention: Find a direct (a vector \(u^{(1)} \in \mathbb{R}\)) onto which to project the data so as to minimize the projection error.

Reudce from 2-dimention to 1-dimention: Find k vectors \(u^{(1)},u^{(2)},...,u^{(k)}\) onto which to project the data so as to minimize the projection error.

PCA同线性回归问题不同的是， PCA的代价函数是找点到投影地的垂直距离。线性回归是预测值与实际值之间的距离。

2.4 Principal Component Analysis Algorithm

2.4.1 Feature scaling/mean nomalization

Training set：\(x^{(1)},x^{(2)},...,x^{(k)}\)
Processing(Feature scaling/mean nomalization)
　\(\mu_j = \frac{1}{m} \sum^{m}_{i=1}x^{(i)}_j\)
　Replace each \(x^{(i)}_j\) with \(x_j - \mu_j\)
　If different features on different scales (e.g \(x_1=\) size of house, \(x_2 =\) number of bedrooms) scale features to have comparable range of values.

2.4.2 PCA

After mean normalization (ensure every feature has zero mean) and optionally feature scaling:

Compute "covariance matrix" ：
　\(\Sigma = \frac{1}{m} XX^T \; (X \in \mathbb{R}^{m \times n})\)

Compute “eigenvectors” of matrix \(\Sigma\)：
　[U, S, V] = svd(Sigma);

\(U = \begin{bmatrix} u^{(1)}& u^{(2)}& \cdots & u^{(n)} \end{bmatrix} \; (U \in \mathbb{R}^{n \times n})\)

　Ureduce = U(:,i:k)
　Z = X * U(:,i:k)

2.5 Reconstruction from Compressed Representation

In some of the earlier videos, I was talking about PCA as a compression algorithm where you may have say, 1,000-dimensional data and compress it to 100-dimensional feature vector. Or have three-dimensional data and compress it to a two-dimensional representation. So, if this is a compression algorithm, there should be a way to go back from this compressed representation back to an approximation of your original high-dimensional data. So given \(z^{(i)}\), which may be 100-dimensional, how do you go back to your original representation, \(x^{(i)}\) or \(x_{approx}^{(i)}\) which was maybe a 1000-dimensional.

X_rec = Z * U(:, 1:k)`

2.6 Choosing the Number of Principal Components

Average squared projection error: \(\frac{1}{m} \sum^{m}_{i=1}||x^{(i)} - x_{approx}^{(i)}\;||^2\)

Total variation in the data: \(\frac{1}{m} \sum^{m}_{i=1} ||x^{(i)}||^2\)

Typically , choose \(k\) to be smallest value so that:

\[\frac{\frac{1}{m} \sum^{m}_{i=1}||x^{(i)} - x_{approx}^{(i)}\;||^2}{\frac{1}{m} \sum^{m}_{i=1} ||x^{(i)}||^2} \leq 0.01 \; \]

We can say that 99% variance retained instead.

这里还有另一种简单的方法来代替上面的方法。利用到了SVD()函数返回的S矩阵。

\[S = \begin{bmatrix} s_{11}& 0 & \cdots & 0\\ 0 & s_{22} & \cdots & 0\\ \vdots & 0 & \ddots & 0\\ 0 & 0 & \cdots & s_{nn}\\ \end{bmatrix} \; (S \in \mathbb{R}^{n \times n})\]

Choose \(k\) to be smallest value so that:

\[\frac{\sum^{k}_{i=1}x_{ii}}{\sum^{n}_{i=1}x_{ii}} \geq 0.99 \]

We can say that 99% variance retained

2.7 Advice for Applying PCA

2.2.1 Supervised learning speedup

If we have a training data set \({(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}), ..., (x^{(m)},y^{(m)})}\).

We can extract inputs to unlabled data which \(x^{(1)},x^{(2)}, ...,x^{(m)} \in \mathbb{R^{10000}}\). Using PCA alogrithem to reudce the data from n-dimention to k-dimention. After that we get \({z^{(1)},z^{(2)}, ...,z^{(m)} \in \mathbb{R^{1000}}}\).

Thus we have a new training set \((z^{(1)},y^{(1)}), (z^{(2)},y^{(2)}), ..., (z^{(m)},y^{(m)})\) to speed up the learning algorithm. Also this operation can reduce memory/disk needed to store data.

Note: Mapping \(x^{(i)} \rightarrow z^{(i)}\)should be defined by running PCA only on the training set. This mapping can be applied as well to the examples \(x^{(i)}_{cv}\) and \(x^{(i)}_{test}\) in the cross valida1on and test sets. Test on test set: Map \(x^{(i)}_{test}\) to \(z^{(i)}_{test}\). Run \(h_\theta (z^{(i)})\) on \((z^{(1)}_{test},y^{(1)}_{test}), (z^{(2)}_{test},y^{(2)}_{test}), ..., (z^{(m)}_{test},y^{(m)}_{test})\).

2.7.2 PCA is sometimes used where it shouldn’t be.

One of the bad use of PCA is that to prevent the overfitting. Use \(z^{(i)}\) instead of \(x^{(i)}\) to reduce the number of features to \(k<n\). Thus fewer features less likely to overfit.

This might work OK but isn't a good way to address overfitting.

Use regularization instead.

\[J(\theta) = - \frac{1}{m} \sum_{i=1}^m [ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2 \]

\[J(\theta) = \frac{1}{m} \sum_{i=1}^m (h_\theta (x^{(i)}) - y^{(i)}) ^2 + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2 \]

Hint: Before implemen1ng PCA first try running whatever you want to do with the original/raw data \(X\) . Only if that doesn't do what you want then implement PCA and consider using \(Z\) .