7-10 电路布线
7-10 电路布线
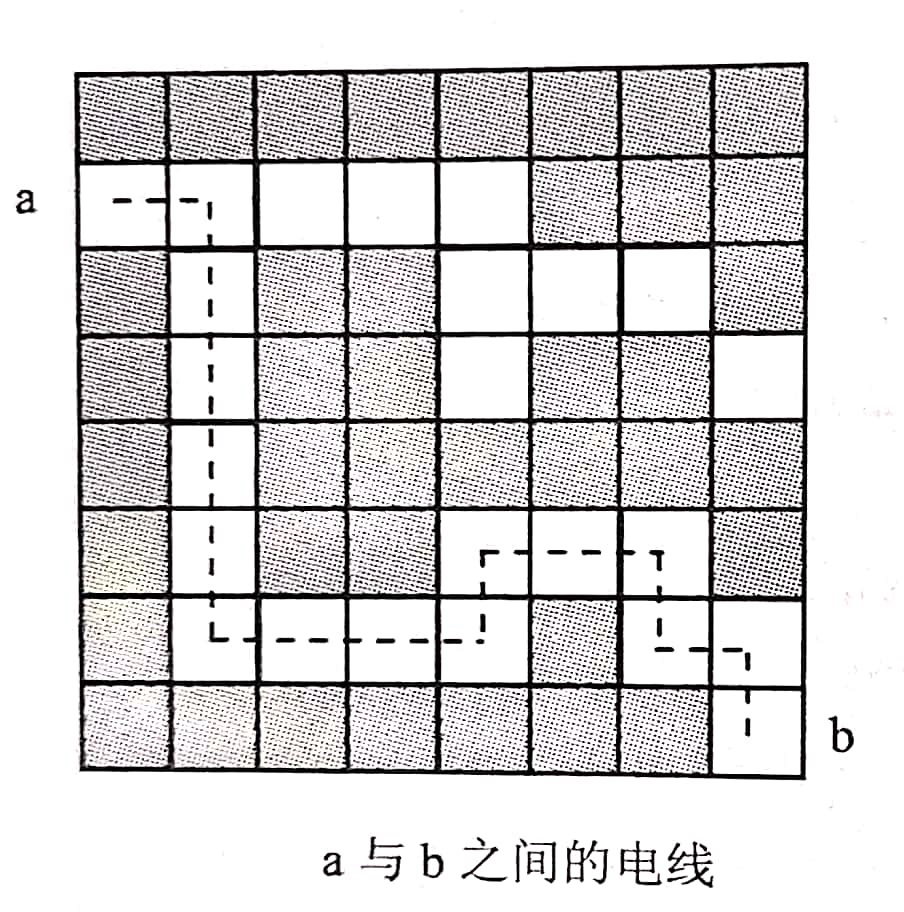
在解决电路布线问题时,一种很常用的方法就是在布线区域叠上一个网格,该网格把布线区域划分成m*n个方格,布线时,转弯处必须采用直角,如已经有某条线路经过一个方格时,则在该方格上不允许叠加布线。如下图所示,如从一个方格a(2,1)的中心点到另一个方格b(8,8)的中心点布线时, 每个方格布线时需要1个单位的电路材料,所需要最少的电路材料是16。
输入格式:
第一行输入网格的m和n
第二行开始输入网格中已经布线的情况,如果已经有布线时,用1表示,尚未布线时,用0表示。
接下来两行分别输入需要布线的起始位置a和结束位置b。
输出格式:
输出从起始位置a到结束位置b布线时所需要的最少电路材料。
输入样例:
在这里给出一组输入。例如:
8 8
1 1 1 1 1 1 1 1
0 0 0 0 0 1 1 1
1 0 1 1 0 0 0 1
1 0 1 1 0 1 1 0
1 0 1 1 1 1 1 1
1 0 1 1 0 0 0 1
1 0 0 0 0 1 0 0
1 1 1 1 1 1 1 0
2 1
8 8
输出样例:
在这里给出相应的输出。例如:
16
简化版代码(c++)
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int mp[N][N], siz[N][N];
bool vis[N][N];
int X[] = {1, 0, -1, 0};
int Y[] = {0, 1, 0, -1};
int main()
{
int n, m;
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
scanf("%d", &mp[i][j]);
}
}
int x1, y1, x2, y2;
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
queue<pair<int, int>> q;
q.push({x1, y1});
vis[x1][y1] = true;
while (q.size()) {
pair<int, int> fr = q.front();
if (fr.first == x2 && fr.second == y2) break;
q.pop();
for (int i = 0; i < 4; ++i) {
int dx = fr.first + X[i];
int dy = fr.second + Y[i];
if (dx < 1 || dx > n || dy < 1 || dy > m) continue;
if (vis[dx][dy] || mp[dx][dy]) continue;
q.push({dx, dy});
siz[dx][dy] = siz[fr.first][fr.second] + 1;
vis[dx][dy] = true;
}
}
printf("%d\n", siz[x2][y2] + 1);
return 0;
}
注释版代码(c++)
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
// 定义网格和距离的数组
int mp[N][N], siz[N][N];
// 记录是否访问过的数组
bool vis[N][N];
// 定义四个方向的数组:下、右、上、左
int X[] = {1, 0, -1, 0};
int Y[] = {0, 1, 0, -1};
int main()
{
// 输入行数和列数
int n, m;
scanf("%d %d", &n, &m);
// 输入网格矩阵
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
scanf("%d", &mp[i][j]);
}
}
// 输入起始和目标位置
int x1, y1, x2, y2;
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
// 创建队列进行广度优先搜索(BFS)
queue<pair<int, int>> q;
q.push({x1, y1});
vis[x1][y1] = true;
// BFS搜索
while (q.size()) {
pair<int, int> fr = q.front();
// 如果当前位置是目标位置,跳出循环
if (fr.first == x2 && fr.second == y2) break;
// 出队
q.pop();
// 遍历四个方向的邻居
for (int i = 0; i < 4; ++i) {
int dx = fr.first + X[i];
int dy = fr.second + Y[i];
// 检查邻居是否在网格范围内
if (dx < 1 || dx > n || dy < 1 || dy > m) continue;
// 检查邻居是否已经访问过或者是障碍物
if (vis[dx][dy] || mp[dx][dy]) continue;
// 入队
q.push({dx, dy});
// 更新距离数组
siz[dx][dy] = siz[fr.first][fr.second] + 1;
// 标记邻居已访问
vis[dx][dy] = true;
}
}
// 输出从起始位置到目标位置的最小距离
printf("%d\n", siz[x2][y2] + 1);
return 0;
}
java版代码
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Main {
static final int N = 1010;
static int[][] mp = new int[N][N];
static int[][] siz = new int[N][N];
static boolean[][] vis = new boolean[N][N];
static int[] X = {1, 0, -1, 0};
static int[] Y = {0, 1, 0, -1};
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 输入行数和列数
int n = scanner.nextInt();
int m = scanner.nextInt();
// 输入网格矩阵
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
mp[i][j] = scanner.nextInt();
}
}
// 输入起始和目标位置
int x1 = scanner.nextInt();
int y1 = scanner.nextInt();
int x2 = scanner.nextInt();
int y2 = scanner.nextInt();
// 创建队列进行广度优先搜索(BFS)
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{x1, y1});
vis[x1][y1] = true;
// BFS搜索
while (!q.isEmpty()) {
int[] fr = q.poll();
// 如果当前位置是目标位置,跳出循环
if (fr[0] == x2 && fr[1] == y2) break;
// 遍历四个方向的邻居
for (int i = 0; i < 4; ++i) {
int dx = fr[0] + X[i];
int dy = fr[1] + Y[i];
// 检查邻居是否在网格范围内
if (dx < 1 || dx > n || dy < 1 || dy > m) continue;
// 检查邻居是否已经访问过或者是障碍物
if (vis[dx][dy] || mp[dx][dy] == 1) continue;
// 入队
q.offer(new int[]{dx, dy});
// 更新距离数组
siz[dx][dy] = siz[fr[0]][fr[1]] + 1;
// 标记邻居已访问
vis[dx][dy] = true;
}
}
// 输出从起始位置到目标位置的最小距离
System.out.println(siz[x2][y2] + 1);
}
}

