2023-2024学年上学期算法设计与分析题期末考试模拟卷
2023-2024学年上学期算法设计与分析题期末考试模拟卷#
注意:该题集非标准答案,仅供参考,如果异议,请在评论区提出或私信。
单选题#
-
()关于分治法描述不正确的是:
A.分治法的基本思想是将规模较大的问题划分为规模较小的子问题来求解。
B.随机生成100个整数并存放在一个数组中,然后从中指定一个整数,则可用二分搜索算法在O(logn)的时间内找到该整数。
C.用分治法求解大整数乘法和Strassen矩阵乘法的基本思想均是通过合理的运算变换来减少乘法的次数。
D.合并排序和快速排序的时间复杂性均为O(nlogn)。
-
( )关于动态规划描述不正确的是:
A.动态规划也是将规模较大的问题划分为规模较小的子问题来求解,但与分治法不同的是,动态规划所划分出来的子问题相互不独立。
B.动态规划算法适用于求解最优化问题,一般采用自底向上的方式来计算。
C.能用动态规划求解的问题就不能使用递归算法求解出来。
D.动态规划求解的问题具有最优子结构和重叠子问题性质。
-
( )关于贪心算法描述正确的是:
A.求解活动安排问题的贪心算法GreedySelector的时间复杂性为
==O(n)==。B.哈夫曼编码是一种最优前缀码,因此对于给定的字符集,各字符编码是唯一的。
C.对于给定的一个带权有向图
G= ( V , E ) ,则可用Dijkstra算法求解出从指定源顶点到其他顶点的最短路长度。D.背包问题(可散装)的贪心算法同样适用于求解0-1背包问题。
-
( )关于回溯法描述正确的是:
A.回溯法即可采用深度优先搜索策略,也可采用广度优先搜索策略。
B.回溯法求解时,可以事先不定义问题的解空间。
C.0-1背包问题的解空间树是一颗排列树。
D.为提高求解效率,使用回溯法时可同时用约束函数和上界函数来剪去一部分子树。
-
( )关于分支限界法描述不正确的是:
A.分支限界法两种常见方法为:队列式分支限界法和优先队列式分支限界法。
B.使用分支限界法时可用约束函数和上界函数来提高搜索效率。
C.在分支限界法中,每个活结点有2个机会成为扩展结点。
D.使用优先队列式分支限界法求解时需要事先明确结点的优先级定义。
-
下面代码段的时间复杂度是( )。
for( i=1; i<2n; i++ ) for ( j=1; j<=n; j++ ) x++;A.
B.
C.
D.
-
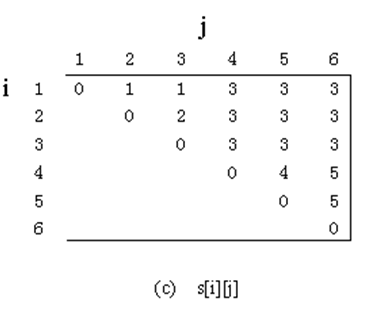
假如需要计算以下6个矩阵的依次连乘:

求解最优乘法次数的递推计算得到如下最优分割位置矩阵s[i][j]:A.1-3分割
B.3-1分割
C.2-2分割
D.0-4分割
-
假如装载问题的两艘轮船B1和B2的承载重量分别是C1和C2(C1>C2),那么解决装载问题可以先解决其中一艘轮船的0-1背包问题,请问选择哪一艘船更合理?
A.选B1更合理
B.选B2更合理
C.选B1或B2都一样
D.装载问题与0-1背包问题无关
-
下列的排序算法使用了分治思想的有()
归并排序
快速排序
选择排序
冒泡排序
A.选择排序
冒泡排序B.归并排序
快速排序C.快速排序
选择排序D.归并排序
冒泡排序
-
若重复进行某种实验,每次实验是互相独立的,且成功的概率为
A.
B.
C.
D.以上全不对
程序填空题#
-
0/1背包问题(回溯法)
#include <stdio.h> #include <string.h> #include <iostream> #define MAXN 20 //最多物品数 using namespace std; int n; //物品数 int W; //限制重量 int w[MAXN]={0}; //存放物品重量,不用下标0元素 int v[MAXN]={0}; //存放物品价值,不用下标0元素 int x[MAXN]; //存放最终解 int maxv; //存放最优解的总价值 void dfs(int i,int tw,int tv,int rw,int op[]) //求解0/1背包问题 { int j; if (i>n) //找到一个叶子结点 { if (____第一空____) //找到一个满足条件的更优解,保存它 { maxv=tv; for (____第二空____) //复制最优解 x[j]=op[j]; } } else //尚未找完所有物品 { if (____第三空____) //左孩子结点剪枝:满足条件时才放入第i个物品 { op[i]=1; //选取第i个物品 dfs(____第四空____); } op[i]=0; //不选取第i个物品,回溯 if (____第五空____) //右孩子结点剪枝 dfs(____第六空____); } } void dispasolution() //输出最优解 { int i; for (i=1;i<=n;i++) if (x[i]==1) printf("%d ",i); printf("\n%d %d",W,maxv); } int main() { int i; cin>>n>>W; //输入物体个数及背包载重量 for(int i=1;i<=n;i++)//输入各物体重量及价值 cin>>w[i]>>v[i]; int op[MAXN]; //存放临时解 memset(op,0,sizeof(op)); int rw=0; for (int i=1;i<=n;i++) rw+=w[i]; dfs(1,0,0,rw,op); dispasolution(); return 0; }输入格式:#
第一行输入背包载重量W及背包个数n,再依次输入n行,每行为背包重量wi和价值vi。
输出格式:#
第一行输出输出装入背包内的物体编号(末尾有空格),第二行输出背包内的物体总重量和总价值。
输入样例1:#
5 10 2 6 2 3 6 5 5 4 4 6输出样例1:#
1 2 3 10 14参考答案:
第一空:
tw==W&&tv>maxv第二空:
j=1;j<=n;j++第三空:
tw+w[i]<=W第四空:
i+1,tw+w[i],tv+v[i],rw-w[i],op第五空:
tw+rw>W第六空:
i+1,tw,tv,rw-w[i],op
主观题#
-
动态规划法与分治法的异同
简述动态规划法与分治法的异同。仅供参考(自己写的)
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划法求解的问题,经分解得到的子问题往往不是互相独立的。若用分治法解这类问题,则分解得到的子问题数目太多,以至于最后解决原问题需要耗费指数时间。然而,不同子问题的数目常常只有多项式量级。在用分治法求解时,有些子问题被重复计算了许多次。如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法。(来自书本P50)
-
简答题-对比说明分支限界法中活结点表的两种组织形式及其特点。
对比说明分支限界法中活结点表的两种组织形式及其特点。仅供参考(自己写的)
1)队列式(FIFO)分支限界法
队列式分支限界法将活结点表组织成一个队列,并按队列的先进先出FIFO(firstin first out)原则选取下一个结点为当前扩展结点。
2)优先队列式分支限界法
优先队列式的分支限界法将活结点表组织成一个优先队列,并按优先队列中规定的结点优先级选取优先级最高的下一个结点成为当前扩展结点。
(来自书本P153)
-
计算题
证明:
-
计算题-矩阵连乘
利用动态规划法计算矩阵连乘积A1A2A3A4A5的最佳求积顺序(即:数乘次数最少的计算次序),各矩阵的维数分别为:
矩阵 A1 A2 A3 A4 A5 维数 5x10 10x3 3x12 12x5 5x50 (要求给出计算步骤)
使用m[i][j]来表示计算从Ai到Aj的矩阵连乘积所需的最少乘法次数。
同时,使用s[i][j]来记录达到最少乘法次数的最后一个乘法操作的位置。动态规划的思路是:
- 对于任意的i,m[i][i] = 0,因为单个矩阵的乘法次数为0。
- 从长度为2的子链开始(即计算A1A2, A2A3, ...),然后逐步增加子链的长度,直到覆盖整个链。
- 对于每个子链Ai...Aj,尝试所有可能的k值(i <= k < j),将子链分为两部分Ai...Ak和Ak+1...Aj,并计算乘法次数。
- 选择乘法次数最小的k值,并更新m[i][j]和s[i][j]。
计算过程如下表所示:
m[i][j]表
i\j 1 2 3 4 5 1 0 150 330 405 1655 2 0 360 330 2430 3 0 180 930 4 0 3000 5 0 s[i][j]表
i\j 1 2 3 4 5 1 0 1 2 2 4 2 0 2 2 2 3 0 3 4 4 0 4 5 0 由表可得出,最佳求积顺序为:
(((A1A2)(A3A4))A5)
附计算过程:
计算过程(以下内容在考试时不需要写): 当 r = 2 时 --- i = 1, j = 2, k = 1 m[1][2] = 5 x 10 x 3 = 150 s[1][2] = 1 --- i = 2, j = 3, k = 1 m[2][3] = 10 x 3 x 12 = 360 s[2][3] = 2 --- i = 3, j = 4, k = 3 m[3][4] = 3 x 12 x 5 = 180 s[3][4] = 3 --- i = 4, j = 5, k = 4 m[4][5] = 12 x 5 x 50 = 3000 s[4][5] = 4 当 r = 3 时 --- i = 1, j = 3 k = 1时 m[1][3] = 5 x 10 x 12 + m[2][3] = 960 k = 2时 m[1][3] = 5 x 3 x 12 + m[1][2] = 330 当 k = 2 时 m[1][3] 最小,故 m[1][3] = 330 s[1][3] = 2 --- i = 2, j = 4 k = 2时 m[2][4] = 10 x 3 x 5 + m[3][4] = 330 k = 3时 m[2][4] = 10 x 12 x 5 + m[2][3] = 960 当 k = 2 时 m[2][4] 最小,故 m[2][4] = 330 s[2][4] = 2 --- i = 3, j = 5 k = 3时 m[3][5] = 3 x 12 x 50 + m[4][5] = 2100 k = 4时 m[3][5] = 3 x 5 x 80 + m[3][4] = 930 当 k = 4 时 m[3][5] 最小,故 m[3][5] = 930 s[3][5] = 4 当 r = 4 时 --- i = 1, j = 4 k = 1时 m[1][4] = 5 x 10 x 5 + m[1][1] + m[2][4] = 580 k = 2时 m[1][4] = 5 x 3 x 5 + m[1][2] + m[3][4] = 405 k = 3时 m[1][4] = 5 x 12 x 5 + m[1][3] + m[4][4] = 630 当 k = 2 时 m[1][4] 最小,故 m[1][4] = 405 s[1][4] = 2 --- i = 2, j = 5 k = 2时 m[2][5] = 10 x 3 x 50 + m[2][2] + m[3][5] = 2430 k = 3时 m[2][5] = 10 x 12 x 50 + m[2][3] + m[4][5] = 6960 k = 4时 m[2][5] = 10 x 5 x 50 + m[2][4] + m[5][5] = 2830 当 k = 2 时 m[2][5] 最小,故 m[2][5] = 2430 s[2][5] = 2 当 r = 5 时 --- i = 1, j = 5 k = 1时 m[1][5] = 5 x 10 x 50 + m[1][1] + m[2][5] = 4930 k = 2时 m[1][5] = 5 x 3 x 50 + m[1][2] + m[3][5] = 1830 k = 3时 m[1][5] = 5 x 12 x 50 + m[1][3] + m[4][5] = 2460 k = 4时 m[1][5] = 5 x 5 x 50 + m[1][4] + m[5][5] = 1655 当 k = 4 时 m[1][5] 最小,故 m[1][5] = 1655 s[1][5] = 4这个过程如果用算法表示是这样的:
a[6] = {5, 10, 3, 12, 5, 50}; for (int i = 1; i <= 5; i++) { m[i][i] = 0; s[i][i] = 0; } for (int r = 2; r <= 5; r++) { for (int i = 1; i <= 5 - r + 1; i++) { int j = i + r - 1; m[i][j] = a[i - 1] * a[i] * a[j] + m[i + 1][j]; s[i][j] = i; for (int k = i + 1; k < j; k++) { int t = m[i][k] + m[k + 1][j] + a[i - 1] * a[k] * a[j]; if (t < m[i][j]) { m[i][j] = t; s[i][j] = k; } } } }
-
算法设计题-马踏棋盘
国际象棋中马的走法相当复杂,现在给定一个8*8的国际象棋棋盘,要求马连续走动若干步,求马的最终位置。马的走法只有两种:1)跳到相邻的格子;2)跳到对角线两格相连的格子。注意,马只能向下和向右走动,且每次只能走一格。设计一种策略,要求每个方格只进入一次,走遍棋盘全部的64个方格,得到马的行走路线。(不需要写出详细代码,只需写出使用的算法策略名称、算法策略、数据准备以及程序实现流程)(15分)
算法策略名称:回溯算法(Backtracking)
算法策略:
- 初始化棋盘,所有格子标记为未访问。
- 选择一个起始位置(例如,左上角)。
- 从起始位置开始,尝试马的所有可能移动。
- 对于每一个移动,检查新的位置是否在棋盘内且未被访问过。
- 如果新的位置有效,则标记该位置为已访问,并递归地尝试从该位置进行下一步移动。
- 如果在尝试所有可能的移动后没有找到解,则回溯到前一步,并尝试其他移动。
- 当找到一条路径,即访问了所有格子时,停止搜索并返回结果。
数据准备:
- 8x8的二维数组,表示棋盘,每个元素初始化为未访问状态。
- 马的当前位置(行和列)。
- 可能的移动列表,根据马的走法生成。
程序实现流程:
-
初始化棋盘和马的位置。
-
调用回溯函数,传入当前位置和棋盘状态。
-
在回溯函数中,检查是否所有格子都已被访问。
-
如果是,则找到了解决方案,返回或记录结果。
-
如果不是,则遍历所有可能的移动。
- 对于每个移动,检查新的位置是否有效。
- 如果有效,更新棋盘状态,递归调用回溯函数。
- 如果递归调用没有找到解,则恢复棋盘状态到移动之前的状态(回溯)。
-
-
如果回溯函数返回,但没有找到解,则整个问题无解。
-
算法设计题-活动安排
某体育馆有一羽毛球场出租,现在总共有10位客户申请租用此羽毛球场,每个客户所租用的开始时间和结束时间如下表所示,其中s(i)表示开始租用时间,f(i)表示结束租用时间:
i 1 2 3 4 5 6 7 8 9 10 s(i) 0 3 1 5 3 5 11 8 8 6 f(i) 6 5 4 9 8 7 13 12 11 10 同一时刻,该羽毛球场只能租给一位客户,请设计一个租用安排方案,在这10位客户里面,使得体育馆尽可能满足多位客户的需求,并算出针对上表的10个客户申请,最多可以安排几位客户申请?
为了解决这个问题,可以使用贪心算法中的“活动选择”策略。基本思想是:每次选择结束时间最早的活动,这样可以为后面的活动留下更多的时间。
具体步骤如下:
-
首先,将10个客户的申请按照结束时间
f(i)进行升序排序。如果两个活动的结束时间相同,则选择开始时间较晚的那个(这样可能会为后面的活动留下更多的时间)。 -
初始化一个空的活动列表,用于存放被选中的活动。
-
从排序后的第一个活动开始,检查每一个活动:
- 如果该活动的开始时间不早于当前活动列表中的最后一个活动的结束时间,则拒绝该活动。
- 否则,将该活动加入到活动列表中。
-
当所有活动都被检查后,活动列表中的活动数量就是最多可以安排的客户数量。
现在,我们来应用这个策略到给定的数据上:
首先,按照
f(i)进行排序,得到以下顺序(这里只列出了被选中的活动,未选中的活动用“X”表示):i 1 2 3 4 5 6 7 8 9 10 原i 3 2 1 6 5 4 10 9 8 7 s(i) 1 3 0 5 3 5 6 8 8 11 f(i) 4 5 6 7 8 9 10 11 12 13 选中 ✓ X X ✓ X X X ✓ X ✓ 按照上述策略,我们选择了以下活动:3, 6, 7, 9。所以最多可以安排4位客户的申请。
-
作者:aslwr
出处:https://www.cnblogs.com/aslwr/p/17948555
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。
各位可以多多推广哦φ(>ω<*)



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!