算法分析与设计 第二次课外作业
一. 单选题（共4题，40分）
-
(单选题)递归通常用( )来实现。
A. 有序的线性表
B. 队列
C. 栈
D. 数组正确答案: C :栈;
10分 -
(单选题)下面关于递归算法的叙述，错误的是( ).
A. 实现递归调用的关键是为算法建立递归调用工作栈
B. 递归算法结构清晰，可读性强
C. 递归算法的运行效率较高，无论是耗费的计算时间还是占用的存储空间都比非递归算法要少
D. 容易用数学归纳法来证明递归算法的正确性正确答案: C :递归算法的运行效率较高，无论是耗费的计算时间还是占用的存储空间都比非递归算法要少;
10分 -
(单选题)
分治法的设计思想是将一个难以直接解决的大问题分割成规模较小的子问题，分别解决子问题，
最后将子问题的解组合起来形成原问题的解和子。这要求原问题和子问题( ）。
A. 问题规模相同，问题性质相同
B. 问题规模相同，问题性质不同
C. 问题规模不同，问题性质相同
D. 问题规模不同，问题性质不同正确答案: C :问题规模不同，问题性质相同;
10分 -
(单选题)分治法所能解决的问题不包含下面的哪一个特征?( )
A. 该问题的规模缩小到一定的程度就可以容易地求解；
B. 该问题可以分解为若干个规模较小的相同问题；
C. 利用该问题分解出的子问题的解可以合并为该问题的解；
D. 原问题所分解出的各个子问题并不独立，它们的解相互依赖。正确答案: D :原问题所分解出的各个子问题并不独立，它们的解相互依赖。;
10分
二. 填空题（共5题，50分）
-
(填空题)一个直接或间接调用自身的算法称为 ____算法。
正确答案：
(1) 递归； -
(填空题)
Hanoi塔问题
如果用hanoi(n,a,b,c)表示将塔座a上自下而上，由大到小叠在一起的n个圆盘依移动规则
移至塔座b上并仍按同样顺序叠放。在移动过程中，以塔座c作为辅助塔座。move(a,b)表示将
塔座a上的圆盘移至塔座b上。由此，可以得到解Hanoi塔问题的递归算法如下：public static void hanoi(int n, int a, int b, int c) { if(n>0) { hanoi(n-1,a,c,b); move(a,b); _____________; } }正确答案：
(1)
hanoi(n-1,c,b,a)； -
(填空题)
出于“平衡子问题”的思想，分治法在分割原问题形成若干子问题时，子问题的规模大致________。正确答案：
(1) 相等；相同 -
(填空题)
分治法的算法设计模式如下：
divide-and-conquer(P) { if(|P|<=n0)adhoc(P); divide P into smaller subinstances P1,P2,…,Pk; for(i=1;i<=k;i++) yi= ; return merge(y1,…,yk); }正确答案：
(1)
divide-and-conquer(Pi)； -
(填空题)
已知一个分治算法耗费的计算时间为T(n), T(n)满足如下递归方程：
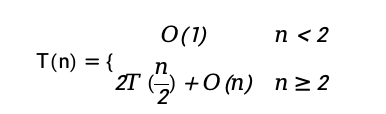解得此递归方程可得T(n)=O(___).正确答案：
(1) nlogn
三. 判断题（共1题，10分）
-
(判断题)在算法设计中，如果用到递归，就不能用分治。
A. 对
B. 错正确答案: 错
10分
