数据结构——5、树——2、B-树/B树

1.1.1 *B-树/B树*

1.1.1.1 *索引为什么使用树结构*

要弄明白B+树，先要弄明白B-树，B-树就是B树，中间的横线不是减号

1、数据库索引为什么要使用树结构进行存储？

树的查询效率高，并且可以保持有序

2、为什么没有使用二叉查找树树来实现？

二叉查找树查询的时间复杂度是O(logN)，从算法逻辑上来讲，二叉查找树的查找速度和比较次数都是最小的，但需要考虑一个现实问题：磁盘IO

数据库索引是存储在磁盘上的，当数据量比较大的时候，索引的大小可能有几个G，甚至更多

当我们利用索引查询的时候，不能将整个索引全部加载到内存中，能做的只有逐一加载每一个磁盘页，这里的磁盘页就对应着索引树的节点

如果利用二叉查找树作为索引结构，假设树的高度是4，查找的值是10，则流程如下：

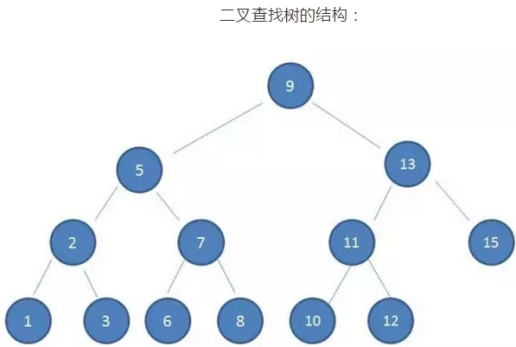
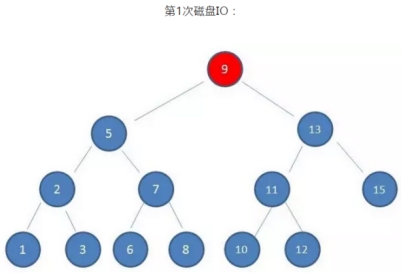
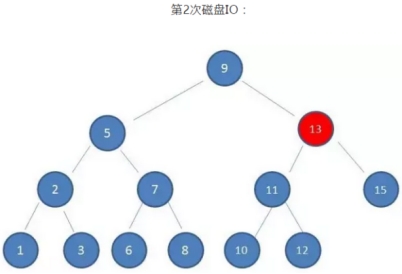
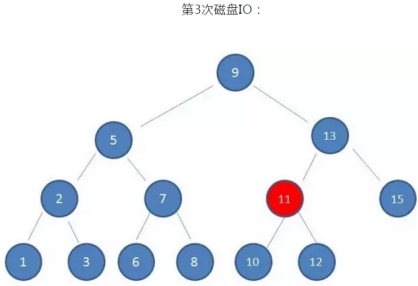
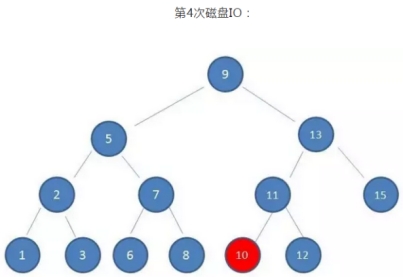
可以看到：

磁盘IO的次数由索引树的高度决定，即最坏查找情况下，磁盘IO的次数等于索引树的高度

为了减少磁盘IO的次数，就需要将将原本“瘦高”的树结构变得“矮胖”，这就是B树的特征之一

1.1.1.2 *B树的特征*

B树是一种多路平衡查找树，它的每一个节点最多包含K个孩子，K被称为B树的阶，K的大小取决于磁盘页的大小

一个m阶的B树具有如下几个特征：

1、 根结点至少有两个子女。

2、 每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m

3、 每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m

4、 所有的叶子结点都位于同一层。

5、 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

示例：以一个3阶B树为例：

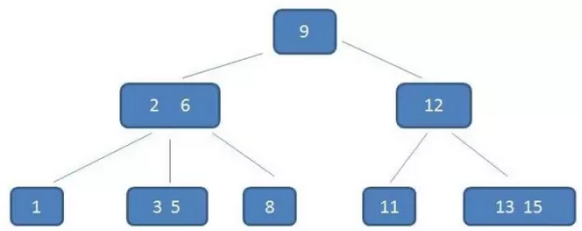
重点看(2,6)节点：

该节点中有两个元素2,6，有三个孩子1，(3,5)，8

其中1小于元素2，(3,5)在元素2,6之间，8大于(3,5)（规则5）

均符合B树的几条特征

1.1.1.3 *B树的查询过程*

B树的查询过程如下：如果B树中查询数值5

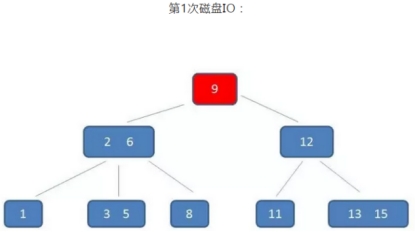
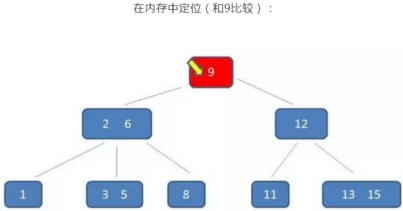
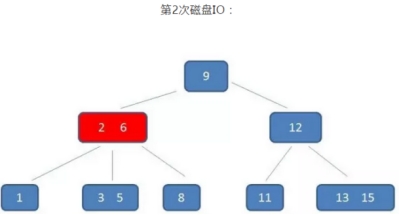
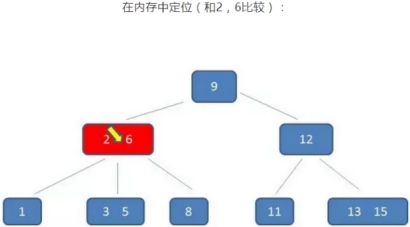
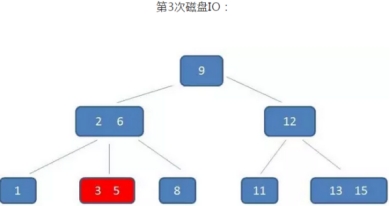
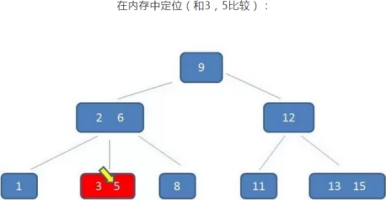
整个流程中，我们可以看出：

B树中的查询次数并不比二叉查找树少，尤其当单一节点中的元素数量很多时，可以相比磁盘IO的速度，内存中的比较耗时，可以忽略不计，

即次数查找是在磁盘IO中查找的，元素比较是在内存中进行的

磁盘读取时，不是按需读取的，而是读取当前数据，并向后读取一段数据，将这段数据加载到内存中，默认这段数据为一页，或页的整数倍，

B树添加节点的时候，默认申请一个磁盘页的空间，用来存储一个节点的数据，这样每个节点只需要一次IO，就可以完全载入

一个节点的数据需要通过一次磁盘IO进行读取，读取到内存中，节点中的数据比较，则是在内存中进行

只要树的高度足够低，IO的次数足够少，就可以提升查找性能。节点内部元素多一些，没有关系，仅仅是多了几次内存交互而已，只要不超过磁盘页的大小即可，这也是B树的优势之一

1.1.1.4 *B树的插入过程*

B树的插入删除过程比较复杂，可以看一个典型的例子：

示例：加入插入的值4：

自顶向下查找4的节点位置，发现4应当插入到节点元素3，5之间。

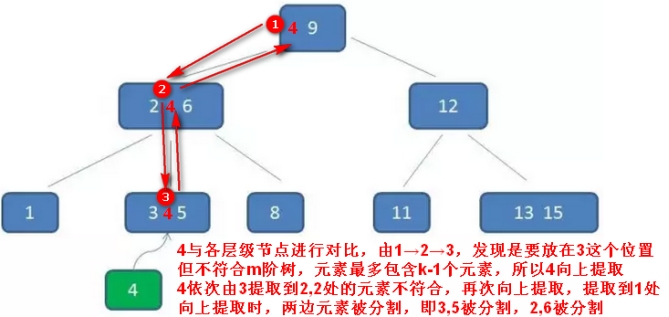
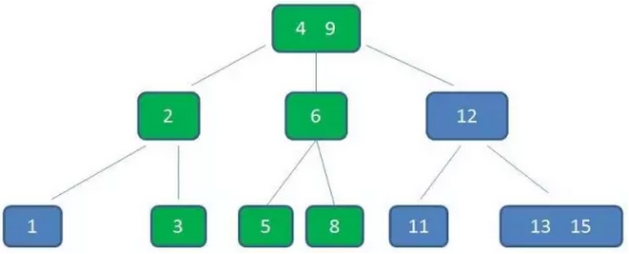
动画演示：https://www.cnblogs.com/vincently/p/4526560.html

可以看到：

为了插入一个元素，整个B树中，很多节点都发生了连锁改变，但这也是B树的一大特点，始终能够维持多路平衡，即自平衡

1.1.1.5 *B树的删除过程*

示例：删除元素11

自顶向下查找元素11的节点位置。

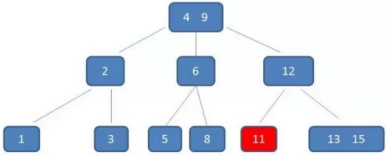
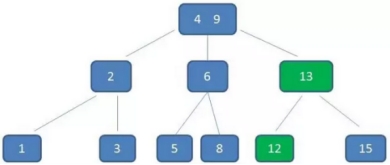
删除11后，节点12只有一个孩子，不符合B树规范。因此找出12,13,15三个节点的中位数13，取代节点12，而节点12自身下移成为第一个孩子。（这个过程称为左旋）

1.1.1.6 *B树的实际应用*

B树主要应用于文件系统，以及部分数据索引，如非关系型数据库MongoDB，大部分关系型数据库，如MySql，使用B+树作为索引