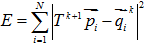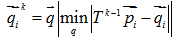基本原理
假定已给两个数据集P、Q, 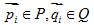 ,给出两个点集的空间变换f使他们能进行空间匹配。这里的问题是,f为一未知函数,而且两点集中的点数不一定相同。解决这个问题使用的最多的方法是迭代最近点法(Iterative Closest Points Algorithm)。
,给出两个点集的空间变换f使他们能进行空间匹配。这里的问题是,f为一未知函数,而且两点集中的点数不一定相同。解决这个问题使用的最多的方法是迭代最近点法(Iterative Closest Points Algorithm)。
基本思想是:根据某种几何特性对数据进行匹配,并设这些匹配点为假想的对应点,然后根据这种对应关系求解运动参数。再利用这些运动参数对数据进行变换。并利用同一几何特征,确定新的对应关系,重复上述过程。
迭代最近点法目标函数
三维空间中两个3D点,
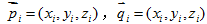 ,他们的欧式距离表示为:
,他们的欧式距离表示为:三维点云匹配问题的目的是找到P和Q变化的矩阵R和T,对于
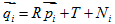 ,
,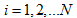 ,利用最小二乘法求解最优解使:
,利用最小二乘法求解最优解使:最小时的R和T。
数据预处理
实验中采集了五个面的点如下所示:
由于第一组(第一排第1个)和第三组(第一排第三个)采集均为模型正面点云,所以选用一和三做后续的实验。
首先利用Geomagic Studio中删除点的工具,去除原始数据中的一些隔离的噪点,效果如下:
平行移动和旋转的分离
先对平移向量T进行初始的估算,具体方法是分别得到点集P和Q的中心:
分别将点集P和Q平移至中心点处:
则上述最优化目标函数可以转化为:
最优化问题分解为:
- 求使E最小的
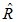
- 求使
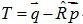
平移中心点的 具体代码为:
- void CalculateMeanPoint3D(vector<Point3D> &P, Point3D &mean)
- {
- vector<Point3D>::iterator it;
- mean.x = 0;
- mean.y = 0;
- mean.z = 0;
- for(it=P.begin(); it!=P.end(); it++){
- mean.x += it->x;
- mean.y += it->y;
- mean.z += it->z;
- }
- mean.x = mean.x/P.size();
- mean.y = mean.y/P.size();
- mean.z = mean.z/P.size();
- }
初始平移效果如下:
利用控制点求初始旋转矩阵
在确定对应关系时,所使用的几何特征是空间中位置最近的点。这里,我们甚至不需要两个点集中的所有点。可以指用从某一点集中选取一部分点,一般称这些点为
控制点(Control Points)。这时,配准问题转化为:
这里,pi,qi为最近匹配点。 在Geomagic Studio中利用三个点就可以进行两个模型的“手动注册”(感觉这里翻译的不好,Registration,应该为“手动匹配”)。
我们将手动选择的三个点导出,作为实验初始的控制点:

对于第i对点,计算点对的矩阵 Ai:
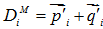
,
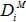
为
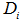
的转置矩阵。
(*这里在査老师的课上给了一个错误的矩阵变换公式)
对于每一对矩阵Ai,计算矩阵B:
- double B[16];
- for(int i=0;i<16;i++)
- B[i]=0;
- for(itp=P.begin(),itq=Q.begin();itp!=P.end();itp++,itq++ ){
- double divpq[3]={itp->x,itp->y,itp->z};
- double addpq[3]={itp->x,itp->y,itp->z};
- double q[3]={itq->x,itq->y,itq->z};
- MatrixDiv(divpq,q,3,1);
- MatrixAdd(addpq,q,3,1);
- double A[16];
- for(int i=0;i<16;i++)
- A[i]=0;
- for(int i=0;i<3;i++){
- A[i+1]=divpq[i];
- A[i*4+4]=divpq[i];
- A[i+13]=addpq[i];
- }
- double AT[16],AMul[16];
- MatrixTran(A,AT,4,4);
- MatrixMul(A,AT,AMul,4,4,4,4);
- MatrixAdd(B,AMul,4,4);
- }
原最优化问题可以转为求B的最小特征值和特征向量,具体代码:
- double eigen, qr[4];
- MatrixEigen(B, &eigen, qr, 4);
- void MatrixEigen(double *m, double *eigen, double *q, int n)
- {
- double *vec, *eig;
- vec = new double[n*n];
- eig = new double[n];
- CvMat _m = cvMat(n, n, CV_64F, m);
- CvMat _vec = cvMat(n, n, CV_64F, vec);
- CvMat _eig = cvMat(n, 1, CV_64F, eig);
-
- cvEigenVV(&_m, &_vec, &_eig);
- *eigen = eig[0];
- for(int i=0; i<n; i++)
- q[i] = vec[i];
- delete[] vec;
- delete[] eig;
- }
-
- void CalculateRotation(double *q, double *R)
- {
- R[0] = q[0]*q[0] + q[1]*q[1] - q[2]*q[2] - q[3]*q[3];
- R[1] = 2.0 * (q[1]*q[2] - q[0]*q[3]);
- R[2] = 2.0 * (q[1]*q[3] + q[0]*q[2]);
- R[3] = 2.0 * (q[1]*q[2] + q[0]*q[3]);
- R[4] = q[0]*q[0] - q[1]*q[1] + q[2]*q[2] - q[3]*q[3];
- R[5] = 2.0 * (q[2]*q[3] - q[0]*q[1]);
- R[6] = 2.0 * (q[1]*q[3] - q[0]*q[2]);
- R[7] = 2.0 * (q[2]*q[3] + q[0]*q[1]);
- R[8] = q[0]*q[0] - q[1]*q[1] - q[2]*q[2] + q[3]*q[3];
- }
平移矩阵计算
2.4中可以得到选择矩阵的4元数表示,由于在"平行移动和旋转的分离"中,我们将最优问题分解为:
- 求使E最小的
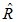
- 求使
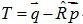
因此还需要通过中心点计算平移矩阵。
- CalculateRotation(qr, R1);
- double mean_Q[3]={_mean_Q.x,_mean_Q.y,_mean_Q.z};
- double mean_P[3]={_mean_P.x,_mean_P.y,_mean_P.z};
- double meanT[3]={0,0,0};
- int nt=0;
- for(itp=P.begin(),itq=Q.begin();itp!=P.end();itp++,itq++ ){
- double tmpP[3]={itp->x,itp->y,itp->z};
- double tmpQ[3]={itq->x,itq->y,itq->z};
- double tmpMul[3];
- MatrixMul(R1, mean_P, tmpMul, 3, 3, 3, 1);
- MatrixDiv(tmpQ,tmpMul,3,1);
- MatrixAdd(meanT,tmpQ,3,1);
- nt++;
- }
- for(int i=0; i<3; i++)
- T1[i] = meanT[i]/(double)(nt);
一次旋转计算得到的矩阵如下:

效果在Geomagic Studio中显示如图:
迭代最近点
在初始匹配之后,所点集P`中所有点做平移变化,在比较点集合P`和Q`的匹配度,(或迭代次数)作为算法终止的条件。 具体为对点集P中每个点,找Q中离他最近的点作为对应点。在某一步利用前一步得到的
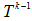
,求使下述函数最小的
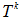
:
这里,
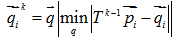
- d = 0.0;
- if(round==1){
- FindClosestPointSet(data,P,Q);
- }
- int pcount=0;
- for(itp = P.begin(),itq=Q.begin();itp!=P.end(); itp++, itq++){
- double sum = (itp->x - itq->x)*(itp->x - itq->x) + (itp->y - itq->y)*(itp->y - itq->y)
- + (itp->z - itq->z)*(itp->z - itq->z);
- d += sum;
- pcount++;
- }
- d=d/(double)(pcount);
循环结束后能得到较好的匹配效果:
封装后的效果图:
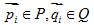 ,给出两个点集的空间变换f使他们能进行空间匹配。这里的问题是,f为一未知函数,而且两点集中的点数不一定相同。解决这个问题使用的最多的方法是迭代最近点法(Iterative Closest Points Algorithm)。
,给出两个点集的空间变换f使他们能进行空间匹配。这里的问题是,f为一未知函数,而且两点集中的点数不一定相同。解决这个问题使用的最多的方法是迭代最近点法(Iterative Closest Points Algorithm)。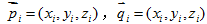 ,他们的欧式距离表示为:
,他们的欧式距离表示为: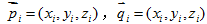 ,他们的欧式距离表示为:
,他们的欧式距离表示为: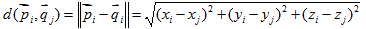
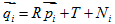 ,
,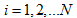 ,利用最小二乘法求解最优解使:
,利用最小二乘法求解最优解使: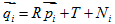 ,
,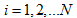 ,利用最小二乘法求解最优解使:
,利用最小二乘法求解最优解使: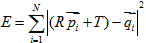



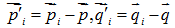
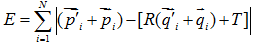
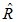
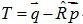

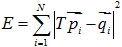





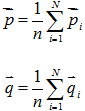
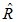
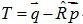
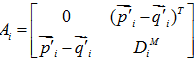
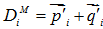 ,
,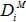 为
为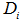 的转置矩阵。
的转置矩阵。
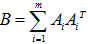
 效果在Geomagic Studio中显示如图:
效果在Geomagic Studio中显示如图:
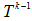 ,求使下述函数最小的
,求使下述函数最小的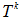 :
: