HDU 3790 最短路径问题 (双重权值)
题目:
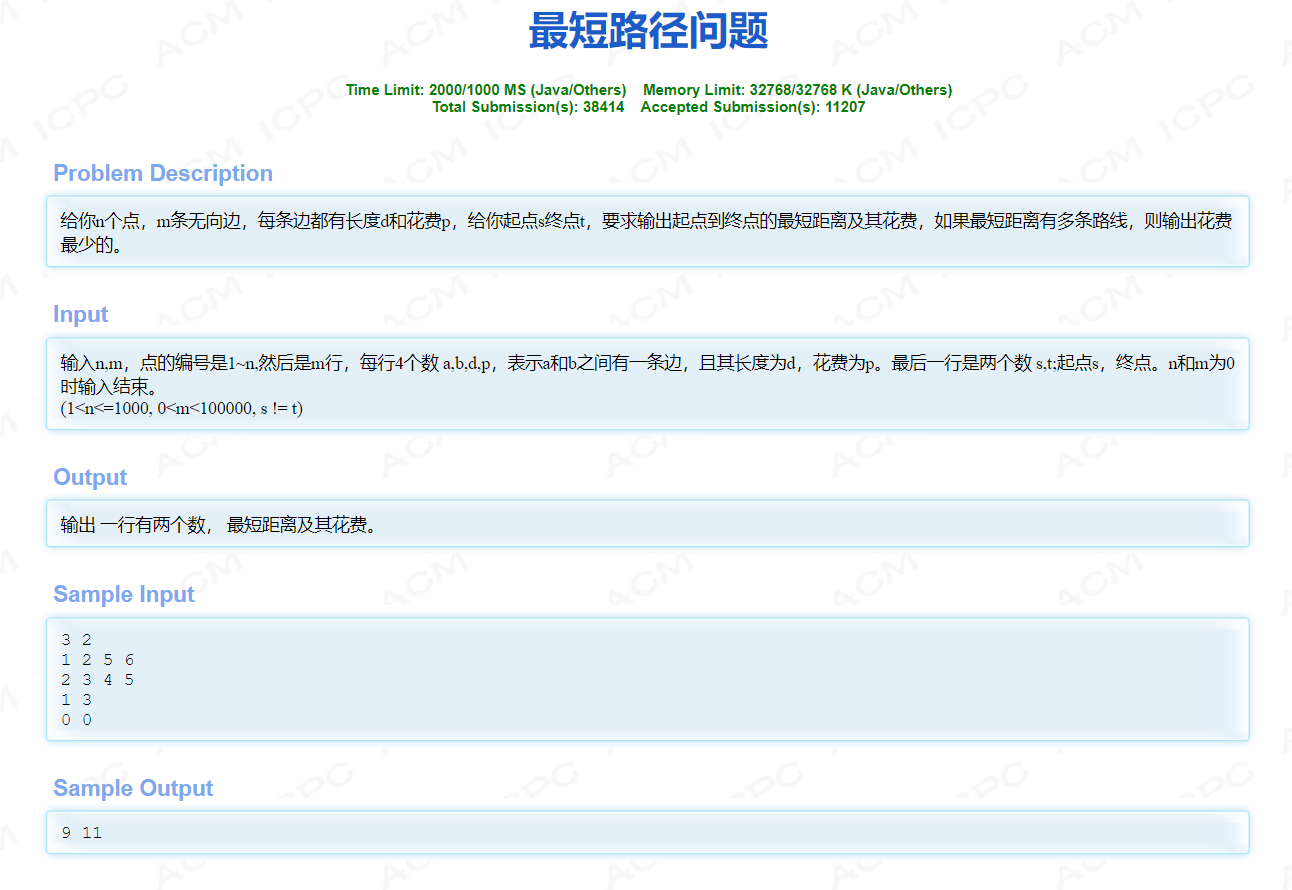
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3790
思路:
此题就是普通的最短路径再加入一个条件(花费最少)。所以只需要修改一下模板就可以了,不过刚写的时候出现的点问题...
下面是我原先Wrong的部分代码:
把两个判断条件合成一个判断条件,其实这样做会出现问题。不可以将花费cost[]也直接作为判断条件,可能存在满足val+dist[q.to]< dist[to]却不满足cost[q.to]+value< cost[to]的状态被忽视的。因为Dijkstra是采用贪心的思想(每次取最小),所以被忽略的状态也有可能是正解。
1 void dijkstra(int start,int endd) 2 { 3 priority_queue<struct v>que; 4 q.to=start,q.val=0,q.value=0; 5 dist[start]=0,cost[start]=0; 6 que.push(q); 7 while(!que.empty()) 8 { 9 q=que.top(); 10 que.pop(); 11 if(!vis[q.to]) 12 { 13 vis[q.to]=true; 14 dist[q.to]=q.val; 15 cost[q.to]=q.value; 16 for(int i=head[q.to];~i;i=edge[i].next) 17 { 18 int to=edge[i].to,val=edge[i].val,value=edge[i].value; 19 if(!vis[to]&&(val+dist[q.to]<=dist[to])&&(value+cost[q.to]<cost[to])) 20 { 21 dist[to]=dist[q.to]+val; 22 cost[to]=cost[q.to]+value; 23 q1.to=to; 24 q1.val=dist[to]; 25 q1.value=cost[to]; 26 que.push(q1); 27 } 28 } 29 } 30 } 31 printf("%d %d\n",dist[endd],cost[endd]); 32 }
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e5+7,inf=0x3f3f3f3f; 4 int head[maxn],cost[maxn],dist[maxn],n,m,a,b,d,p,start,endd,tot; 5 bool vis[maxn]; 6 struct v 7 { 8 int from,to,next,val,value; 9 }edge[maxn],q,q1; 10 void init() 11 { 12 for(int i=1;i<=n;i++) 13 { 14 vis[i]=false; 15 head[i]=-1; 16 dist[i]=inf; 17 cost[i]=inf; 18 } 19 tot=0; 20 } 21 bool operator <(struct v a,struct v b) 22 { 23 if(a.val==b.val) 24 return a.value>b.value; 25 else 26 return a.val>b.val; 27 } 28 void add_edge(int from,int to,int val,int value) 29 { 30 edge[tot]=(v) 31 { 32 from,to,head[from],val,value 33 }; 34 head[from]=tot++; 35 } 36 void dijkstra(int start,int endd) 37 { 38 priority_queue<struct v>que; 39 q.to=start,q.val=0,q.value=0; 40 dist[start]=0,cost[start]=0; 41 que.push(q); 42 while(!que.empty()) 43 { 44 q=que.top(); 45 que.pop(); 46 if(!vis[q.to]) 47 { 48 vis[q.to]=true; 49 dist[q.to]=q.val; 50 cost[q.to]=q.value; 51 for(int i=head[q.to];~i;i=edge[i].next) 52 { 53 int to=edge[i].to,val=edge[i].val,value=edge[i].value; 54 if(!vis[to]&&val+dist[q.to]<dist[to])///正常最短路处理; 55 { 56 dist[to]=dist[q.to]+val; 57 cost[to]=cost[q.to]+value; 58 q1.to=to; 59 q1.val=dist[to]; 60 q1.value=cost[to]; 61 que.push(q1); 62 } 63 else if(!vis[to]&&val+dist[q.to]==dist[to])///多条最短路处理; 64 { 65 cost[to]=min(cost[to],cost[q.to]+value); 66 q1.to=to; 67 q1.val=dist[to]; 68 q1.value=cost[to]; 69 que.push(q1); 70 } 71 } 72 } 73 } 74 printf("%d %d\n",dist[endd],cost[endd]); 75 } 76 int main() 77 { 78 while(~scanf("%d%d",&n,&m), n||m) 79 { 80 init(); 81 while(m--) 82 { 83 scanf("%d%d%d%d",&a,&b,&d,&p); 84 add_edge(a,b,d,p); 85 add_edge(b,a,d,p); 86 } 87 scanf("%d %d",&start,&endd); 88 dijkstra(start,endd); 89 } 90 }


