机器学习 - 编程练习（一）：线性回归

编程练习（一）：线性回归

---

文件清单

• ex1.m
• ex1_multi.m
• ex1data1.txt - ex1.m 用到的数据组
• ex1data2.txt - ex1_multi.m 用到的数据组
• submit.m - 提交代码
• [*] warmUpExercise.m
• [*] plotData.m
• [*] computeCost.m
• [*] gradientDescent.m
• [+] computeCostMulti.m
• [+] gradientDescentMulti.m
• [+] featureNormalize.m
• [+] normalEqn.m

* 为必须要完成的
+ 为可选

1 简单的Octave/MATLAB函数

完成 warmUpExercise.m ，使得 A 为 5x5 单位矩阵，送分的。

A = eye(5); 

输出结果：

ans =
Diagonal Matrix
	1 	0 	0 	0 	0
	0 	1 	0 	0 	0
	0 	0 	1 	0 	0
	0 	0 	0 	1 	0
	0 	0 	0 	0 	1

1.1 提交代码

使用 submit

解决不能上传的问题：

Windows

进入练习的 /lib 文件夹中，编辑 submitWithConfiguration.m 修改第66行，然后重启octave

responseBody = urlread(submissionUrl, 'post', params);
% 改为
[code, responseBody] = system(sprintf('echo jsonBody=%s | curl -k -X POST -d @- %s', body, submissionUrl));

OSX Linux

进入练习的 /lib 文件夹中，编辑 submitWithConfiguration.m 修改第66行，然后重启octave

responseBody = urlread(submissionUrl, 'post', params);
% 改为
[code, responseBody] = system(sprintf('echo ''jsonBody=%s'' | curl -k -X POST -d @- %s', body, submissionUrl));

2 单变量线性回归

背景：假设我们现在是个连锁餐厅的老板，已经在很多城市开了连锁店（提供训练组），现在想再开新店，需要通过以前的数据预测新开的店的收益。

ex1data1.txt 提供所需要的训练组，第一列是城市人口，第二列是对应的收益。负值代表着亏损。

ex1.m 已经加载了数据。

2.1 可视化数据

ex1.m 中加载了变量 X 和 y：

data = load('ex1data1.txt'); % read comma separated data
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples

接着 plotData 函数将其绘制出来，我们需要完成 plotData.m 进行绘图：

plot(x, y, 'rx', 'MarkerSize', 10); % Plot the data
ylabel('Profit in $10,000s'); % Set the y-axis label
xlabel('Population of City in 10,000s'); % Set the x-axis label

现在运行 ex1.m 就能看到类似图1的图像了：

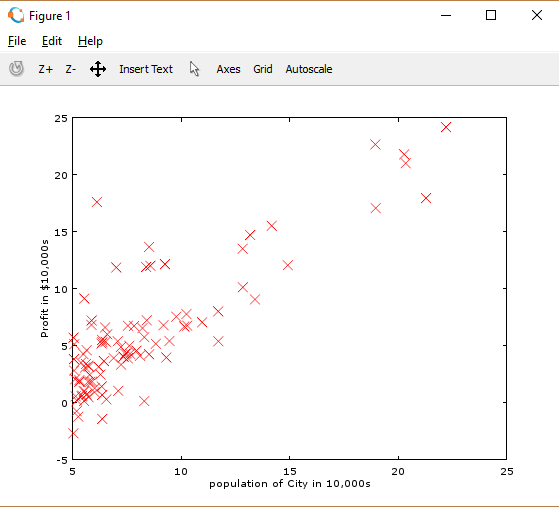
* 通过看手册学习函数是个很好的方式 help plot 。

2.2 梯度下降

在这一结中我们要通过梯度下降计算出合适的线性回归参数theta。

2.2.1 更新等式

线性回归的目标是将成本函数最小化：

\[J(\theta) = \frac{1}{2m}\sum_{i=1}^m (h_{\theta}(x_{i})-y_{i})^{2} \]

其中线性模型的假设 \(h_\theta(x)\) 为：

\[h(x) = \theta_{0} + \theta_{1}x \]

记住我们的变量是 \(\theta\) ，通过调整 \(\theta\) 的值来最小化成本函数。一种方式就是梯度下降，每次迭代都会更新 \(\theta\) ：

\[\theta_{j} := \theta_{j} - \alpha\frac{1}{m}\sum_{i=1}^m ((h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}) \]

* 与 = 不同，:= 代表着 同时更新(simultaneously update)，简单来说就是先将计算的 \(\theta\) 存入一个临时变量，最后所有 \(\theta\) 都计算完了一起再赋值回去。

例如：

temp1 = theta1 - （theta1 - 10 * theta2 * x1） ;
temp2 = theta2 - （theta1 - 10 * theta2 * x2） ;
theta1 = temp1 ;
theta2 = temp2 ;

注意，我们使用梯度下降时在矩阵 X 第一列增加了一列 1

X = [ones(m, 1), data(:,1)]; % Add a column of ones to x

原因是成本函数的公式中 \(\theta_0\) 的系数为1.

2.2.2 工具

X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
iterations = 1500;
alpha = 0.01;

初始化 theta ，迭代次数 iteration ，Learning rate alpha 。

2.2.3 计算成本函数

在这一节我们需要根据成本函数完成 computeCost.m，注意 X，y是训练组中的数据矩阵而不是非矢量数(scalar values)。

当正确完成成本函数后，ex1.m 下一步将 theta 初始化为0，运行成功后会输出结果 32.07 。

* 完成后使用 submit 提交代码。

参考代码：

% ====================== YOUR CODE HERE ===================================

J = sum((X*theta-y).^2)/(2*length(y));

% =========================================================================

2.2.4 梯度下降

接下来我们需要完成 gradientDescent.m 。其中循环结构已经写好了，仅需要写每次更新 theta 的函数即可。

编程时要明确的知道，成本函数J是改变 theta 来最小化的，而不是 X 或者 y。

怎么样验证自己的梯度下降工作正常？

可以通过在循环中打印 computeCost 的结果，如果梯度下降工作正常，则打印的结果应该慢慢减少然后无变化。

完成函数后，ex1.m将会使用最后的theta绘制出一条匹配的直线。如图：

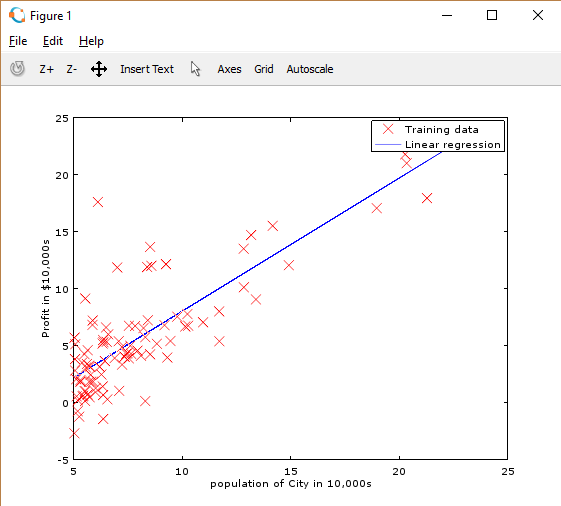
最后得到的 \(\theta\) 我们用来预测人口 35,000 和 70,000 地区的收益。

* 完成后使用 submit 提交代码。

*注意，Octave/MATLAB中 A*B 默认为矩阵乘法，使用 A.*B 可以用逐元素乘法。

参考代码：

% ====================== YOUR CODE HERE ======================

theta = theta - X'*(X*theta-y)/m*alpha;

% ============================================================

2.4 可视化成本函数

为了更好的理解成本函数，在这一节我们将构建一个三维的图形。

ex1.m 中已经写好了这一部分的代码，但是我们需要理解为什么代码这么写。

% initialize J vals to a matrix of 0's
J vals = zeros(length(theta0 vals), length(theta1 vals));
% Fill out J vals
for i = 1:length(theta0 vals)
	for j = 1:length(theta1 vals)
		t = [theta0 vals(i); theta1 vals(j)];
		J_vals(i,j) = computeCost(x, y, t);
	end
end

通过 computeCost 函数，我们计算出对应的值并储存到一个以 theta0 和 theta1 为坐标的矩阵 J_vals 中

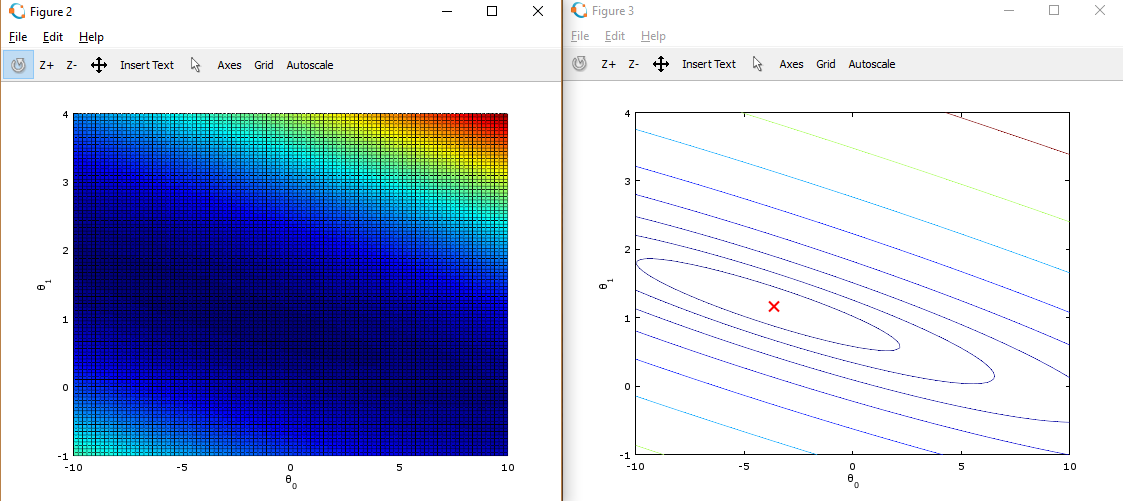
通过使用 surf 和 contour 命令，我们可以构建出图形：

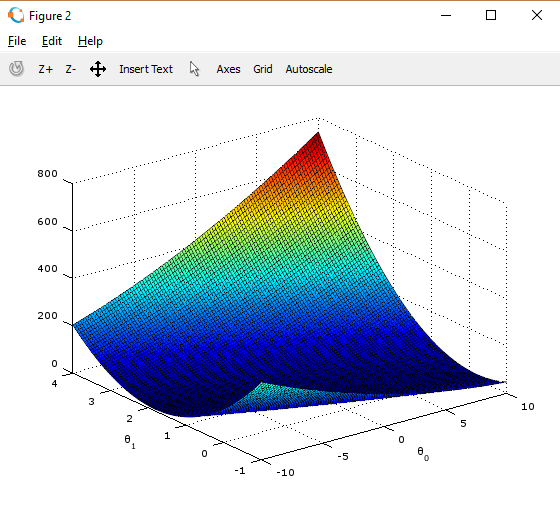
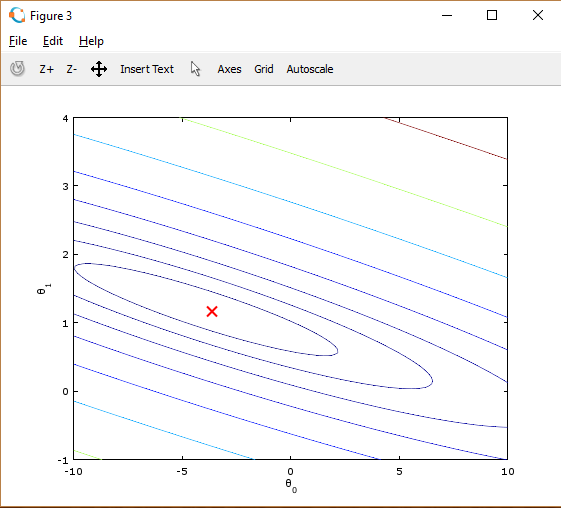
这些图像的目的是为了展示 \(J(\theta)\) 随着 \(\theta_0\) 和 \(\theta_1\) 的改变的值。（在2D轮廓图中比3D的更直观）。最小点是 \(\theta_0\) 和 \(\theta_1\) 的最适点， 每一步梯度下降都会更靠近这个点。

我们可以通过旋转看到为什么叫“轮廓图”：

附加练习

---

3 多元线性回归

在这一节中，我们将会利用多元线性回归预测房子的价格。假设我们要出售我们的房子，现在想知道在房市中能卖一个什么价格。一种方式是收集最近出售的房价数据，构建一个房子价格的模型。

ex1data2.txt中包含了房子价格的训练组。第一列是房子的尺寸（平方英尺），第二列是卧室的数量，第三列是房子的价格。

我们通过 ex1_multi.m 完成本次任务。

3.1 特性一般化(Feature Normalization)

首先我们需要用特性放缩让数据的范围缩小，使得梯度下降计算的更快：

我们的任务是完成 featureNormalize.m：

• 计算每个特性的平均值(mean)
• 计算标准差(standard deviations)
• 特性放缩(feature scaling)

* 我们这里利用的是标准差(standard deviation)，也可以使用差值(max - min)。

* 完成后使用 submit 提交代码。

参考代码：

% ====================== YOUR CODE HERE ======================   

mu = mean(X);
sigma = std(X);
X_norm = (X - mu) ./ sigma;

% ============================================================

3.2 梯度下降

我们之前用梯度下降解决单变量线性回归问题，和多元线性回归问题的唯一区别就是矩阵 X 的特性不止一个，假设函数的公式没有变化。

我们需要完成 computeCostMulti.m 和 gradientDescentMulti.m 完成多元线性回归的成本函数和梯度下降。如果之前的梯度下降适用于多变量，这里也可以使用。

* 确保代码支持多个特性，而且满足向量运算条件。可以使用 size(X, 2) 找出训练组中有多少特性。

* 完成后使用 submit 提交代码。

* 多变量中， 成本函数也可以写成向量计算形式：

\(J(\theta) = \frac{1}{2m} (X\theta - \vec{y})^{T} (X\theta - \vec{y})\）

参考代码：

% ====================== YOUR CODE HERE ======================

theta = theta - X'*(X*theta-y)/m*alpha;

% ============================================================

3.2.1 附加练习：学习速率的选择（Learning rate）

对于不同的训练组，选择合适的学习速率可以使得结果计算的更快更准确。我们可以在 ex1_multi.m 中修改 alpha 值。

实际经验我们可以一步一步的改变值，例如 0.3 -> 0.1 -> 0.03 -> 0.01 等等。

不合适学习速率

过大：导致找不到最适点，Octave/MATLAB会返回一个 NaNs 代表 not a number ，也就是正无穷或者负无穷。

成本函数和迭代次数的图形如下：

（！图片）

过小：导致梯度下降计算耗时严重。

合适的学习速率

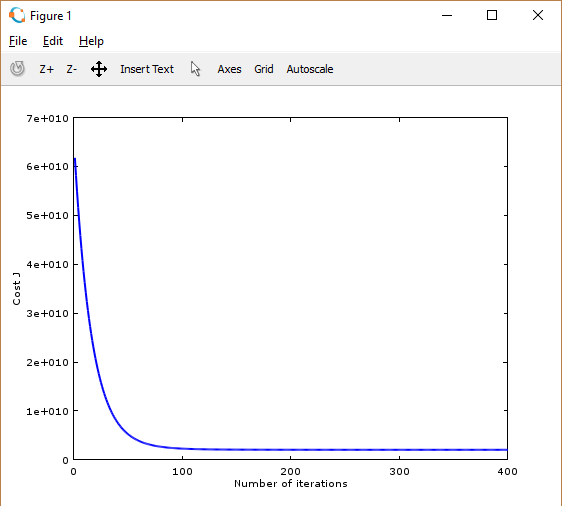
接下来，我们需要用训练好的 theta 值来预测 1650 平方英尺 3 个卧室的房子的价格。

注意不要忘记放缩！

参考代码：

% ====================== YOUR CODE HERE ======================
P = [1 (([1650 3] - mu) ./ sigama)];
price = P*theta;
% ============================================================

3.3 一般等式

这一结我们需要完成 normalEqn.m 利用公式：

\(\theta = (X^T X)^{-1}XT y\)

完成之后我们可以预测 1650 平方英尺 3 个卧室的房子的价格。

参考代码：

% ====================== YOUR CODE HERE ======================
price = 1650; % You should change this
price = [1,1650,3]*theta;
% ============================================================