本章的目的是学会使用神经网络来解决实际问题。
3.1 神经网络剖析
训练神经网络主要围绕以下几个方面:
(1)层,多个层组合成网络。
(2)输入数据和相应的目标
(3)损失函数,即用于学习的反馈信号
(4)优化器,决定学习过程如何进行。
这四者的关系如下图所示:
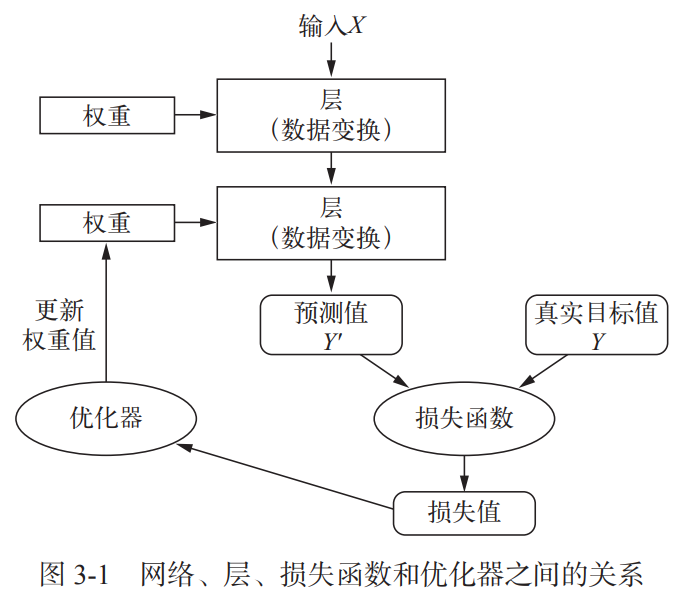
3.1.1 层:深度学习的基础组件
层是神经网络的基本数据结构,是一个数据处理模块,将一个或多个输入张量转换为一个或多个输出张量。
权重是利用随机梯度下降学到的一个或多个张量,包含网络的知识。
1 from keras import layers 2 3 layer = layers.Dense(32, input_shape=(784,))
以上代码创建了一个层,接受第一个维度大小为784的2D张量。
解释:input_shape=(784,),表示输入的张量是一个矩阵(2D张量),这个矩阵有784行,可以有任意的列。
假设只有1列,那就是一个784行,1列的向量(1D张量)。这就是MNIST中的一个样本,即28 * 28大小的一张图片,将其从左上角开始,先行后列的每一个像素拼接成一个784维的列向量。
假设有batch_size列,那就是一个784行,batch_size列的矩阵,矩阵中每一列都是将一个28 * 28的样本“展开”而获得的列向量。
from keras import models from keras import layers model = models.Sequential() model.add(layers.Dense(32, input_shape=(784,))) model.add(layers.Dense(32))
输入层接收的是784 * batch_size的矩阵,因此输入层是一个784个节点的神经层,使用liner激活,输出的是一个32维向量(1D张量)。
第一层是一个32个节点的神经层,使用liner激活,输出的是也给32维向量(1D张量)。
第二层没有明确输入形状,但是可以从上一层的输出自动推测出它是一个32个节点的神经层,使用liner激活,但没有明确输出的形状。
举例分析:假设batch_size=128,则输入数据X是一个784 * 128的矩阵,输入层是一个784维的向量,输入层在进行计算时,先从矩阵X中取出一列,记作Xi0,这是一个784维的向量,为方便表示,令Y1 = Xi0。第一层有32个节点,Y1是一个784维向量,也可以看作1行,784列的矩阵。
同时这一层存储了一个权重矩阵W1,它是一个784行,32列的矩阵,偏执向量b1是一个32维向量。
第一层的计算方式为:Y2 = Y1.dot(W1) + b1,
就是用Y1的第一个元素与W1的第一列中的每个元素相乘(784对),再将这784个数相加,然后再加上偏执向量(32维)b1的第一个元素的值,这样就得到了Y2的第一个元素。
然后用Y1的第二个元素与W1的第二列中的每个元素相乘(784对),再将这784个数相加,然后再加上偏执向量(32维)b1的第二个元素的值,这样就得到了Y2的第二个元素。
……
这种计算进行32次,最终得到的Y2是一个32维的向量,也可以看作1行32列的矩阵。
第二层的计算方式为:Y3 = Y2.dot(W2) + b2,Y2是一个32维向量,也可以看作一个1行32列的矩阵,W2是一个32行32列的矩阵,偏执向量b2是一个32维向量。
就是用Y2的第一个元素与W2的第一列中的每一个元素相乘(784对),再将这784个数相加,然后再加上偏执b2的第一个元素的值,这样就得到了Y3的第一个元素。
然后用Y2的第二个元素与W2的第二列中的每一个元素相乘(784对),再将这784个数相加,然后再加上偏执b2的第二个元素的值,这样就得到了Y3的第二个元素。
……
这种计算进行32次,最终得到的Y3是一个32维的向量,也可以看作1行32列的矩阵。
如此就完成了一个样本的计算。得到了第一个样本在这个网络的输出值。将这个输出值暂存起来。
接着从输入X中选择第二列(第二个样本),按照上述流程也进行计算,得到第二个样本的输出值。
一直到将第128个样本计算完毕,最终得到128个向量,每个向量是32维的。
无论指定哪种损失函数,都可以采用求平均的方式进行处理,就是将这一个批次128个样本的损失求值求平均,然后用这个平均的损失进行反向传播,修正每一层的权重,以使得损失略微减小。
3.1.2 模型:层构成的网络
深度学习模型是层构成的有向无环图,网络的拓扑结构定义了一个假设空间。
机器学习的一种定义:在预先定好的可能性空间中,利用反馈信号的指引来寻找输入数据的有用表示。
选择网络拓扑结构,意味着将可能性空间(假设空间)限定为一系列特定的张量运算,将输入数据映射为输出数据。然后为这些张量运算的权重张量找到一组合适的值。
3.1.3 损失函数与优化器:配置学习过程关键
损失函数——在训练过程中需要将其最小化,它能衡量当前任务是否已成功完成。
优化器——决定如何基于损失函数对网络进行更新。它执行的是随机梯度下降的某个变体。
对于二分类问题:可以使用二元交叉熵损失函数。
对于多分类问题:可以使用分类交叉熵损失函数。
对于序列学习问题:可以使用联结主义时序分类损失函数。




