2.1初识神经网络
使用Python的Keras库,编写手写数字识别(MNIST)的代码如下:
1 import tensorflow as tf 2 from keras import models 3 from keras import layers 4 5 from keras.datasets import mnist 6 from keras.utils import to_categorical 7 8 #1. 获取数据集 9 (train_images, train_labels), (test_images, test_labels) = mnist.load_data() 10 11 #2. 处理数据集 12 train_images = train_images.reshape((60000, 28 * 28)) 13 train_images = train_images.astype('float32') / 255 14 15 test_images = test_images.reshape((10000, 28 * 28)) 16 test_images = test_images.astype('float32') / 255 17 18 train_labels = to_categorical(train_labels) 19 test_labels = to_categorical(test_labels) 20 21 #3. 建立网络模型 22 network = models.Sequential() 23 network.add(layers.Dense(512,activation='relu',input_shape=(28 * 28,))) 24 network.add(layers.Dense(10,activation='softmax')) 25 26 #4. 设置编译三参数 27 network.compile(optimizer='rmsprop', 28 loss='categorical_crossentropy',metrics=['accuracy']) 29 30 #5. 设置训练条件 31 network.fit(train_images, train_labels, epochs=5, batch_size=128) 32 33 #6. 训练模型并评估模型 34 test_loss, test_acc = network.evaluate(test_images, test_labels) 35 print('test_acc', test_acc)
2.2神经网络的数据表示
张量(Tensor):numpy的ndarray数据类型中存储的是张量。张量的维度叫做轴,轴从0开始计数。
标量(0D 张量):仅包含一个数字的张量叫做标量,标量有0个轴。
1 import numpy as np 2 3 x1 = np.array(1) 4 print(type(x1)) # <class 'numpy.ndarray'> 5 print(x1.shape) # () 6 print(x1.ndim) # 0
向量(1D 张量):数字组成的数组叫做向量,向量有1个轴。
1 import numpy as np 2 3 x2 = np.array([1, 2,3,4,5]) 4 print(x2.shape) # (5,) 5 print(x2.ndim) # 1
x2是一个5D向量,但它是一个1D的张量。它只有1个轴,但是这个轴上有5个维度。
矩阵(2D张量):向量组成的数组叫矩阵,矩阵有2个轴。
1 import numpy as np 2 3 x3 = np.array([[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15]]) 4 print(x3.shape) # (3, 5) 5 print(x3.ndim) # 2
x3是一个3行2列的矩阵。
3D张量与更高维张量:将多个矩阵组合成一个新的数组,就是3D张量。3D张量有3个轴。
shape值为:(矩阵个数, 矩阵的行数, 矩阵的列数)
张量的数据类型(dtype),一般情况下是:float32、uint8、float64,也可能是char类型。但不能是字符串张量。
注:一般在深度学习中使用的张量,其第一个轴(0轴)都是批量轴,因此张量的维度比数据本身,要多一维。
2.3 神经网络的“齿轮”:张量运算
逐元素运算:常见的有逐元素的加法,逐元素的乘法,relu()运算等。
在numpy底层,逐元素运算使用BLAS实现(一般由C编写的函数库),而不是普通的循环遍历。
广播:
(1)向较小的张量添加轴,使其ndim与较大的张量相同。
(2)将较小的张量沿着新轴重复,使其形状与较大的张量相同。
张量点积:点积运算也叫张量积。
两个向量的点积:对应维度的元素相乘,再相加,最终结果是一个标量。
1 import numpy as np 2 3 x = np.array([1,2,3]) 4 y = np.array([4,5,6]) 5 6 z = x.dot(y) 7 print(z) # 32
计算方式如下:(1 * 4 ) + (2 * 5) + (3 * 6)= 4 + 10 + 18 = 32
矩阵与向量的点积,返回一个向量。注意:“矩阵点积向量”的结果与“向量点积矩阵”的结果是不同的。
1 import numpy as np 2 3 A = np.array([[1,2],[3,4]]) 4 x = np.array([5,6]) 5 6 y1 = A.dot(x) 7 print(y1) # [17 39] 8 9 y2 = x.dot(A) 10 print(y2) # [23 34]
A.dot(x)的计算方式:[(1 * 5) + (2 * 6) , (3 * 5) + (4 * 6)] = [17, 39]
而x.dot(A)的计算方式:[(1 * 5) + (3 * 6),(2 * 5) + (4 * 6)] = [23, 34]
两个矩阵的点积(矩阵乘法),假设A和B是两个矩阵,A.dot(B)要需要满足条件:A的1轴的维度 = B的0轴的维度,也就是A的列数 = B的行数。
其结果是一个(A.shape[0], B.shape[1])形状的矩阵(A的行数,B的列数)。
张量变形:是指改变张量的行和列,以得到想要的形状,变形后的张量的元素总个数与初始张量相同。
例如shape=(2,3)的格式变为:shape(3,2)的,也可以变成shape(1,6)或shape(6,1)的张量。
1 import numpy as np 2 3 A = np.array([[[1,2],[3,4]],[[5,6],[7,8]]]) 4 print(A.shape) # (2, 2, 2) 5 6 B = A.reshape((2,4)) 7 print(B) # [[1 2 3 4] [5 6 7 8]]
张量变形可以改变张量的维度。
2.4 神经网络的“引擎”:基于梯度的优化
一个训练循环的步骤如下:
(1) 抽取训练样本x和对应目标y组成的数据批量。
(2) 在x上运行网络[这一步叫做前向传播],得到预测值y_pred。
(3) 计算网络在这批数据上的损失,用于衡量y_pred和y之间的距离。
(4) 更新网络的所有权重,使网络在这批数据上的损失略微下降。
什么是导数
“导数完全描述了改变x后f(x)会如何变化。如果你希望减小f(x)的值,只需将x沿着导数的反方向移动一小步。”这句话的解释:
反方向就是符号相反的意思。
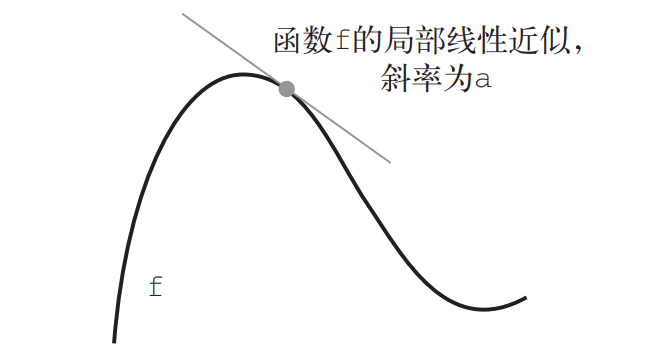
见上图,根据数学知识可知,函数y=f(x)在当前点p的斜率为负值。要想使得f(x)的值减小,则需要让p点"向右"移动,也就是增大x的值。
也就是x需要加上一个正数。而p点的斜率(导数)是负数。这两个数字的符号相反,也就是方向相反。
张量运算的导数:梯度
梯度是张量运算的导数。它是导数这一概念向多元函数导数的推广。多元函数是以张量作为输入的函数。
假设有一个输入向量x、一个矩阵(2D导数)W、一个目标y和一个损失函数loss。你可以用W来计算预测值y_pred,然后计算损失。
1 y_pred = dot(W, x) 2 loss_value = loss(y_pred, y)
这里x和y是样本的属性及其标签,虽然这里用的是x和y,但这两个向量在训练模型时都是已知的数值,而可以其看作是W映射到损失值得函数。
1 loss_value = f(W)
这里自变量W不再是一个标量(0D张量),而是一个矩阵(2D张量)。假设这个矩阵W有m行和n列。那么这就是一个m * n元的函数。
假设W的当前值是W0 它是一个矩阵,在W0 的导数是一个与W形状相同的矩阵(2D张量)表示为gradient(f)(W0),
grandient(f)(W0)的每一个值grandient(f)(W0)[i, j] ,都表示改变W0[i,j]时loss_value变化的方向和大小,也就是偏导数。
这个gradient(f)(W0)可以看作f(W)在W0附近的曲率的矩阵,这个矩阵就是梯度。
与标量类似,矩阵也是有“方向”的,只是这个方向不能在三维的空间中展示出来。
可以通过将W向梯度的反方向移动一小步来减小f(W)的值。
随机梯度下降
小批量随机梯度下降(MBGD):每次抽取训样本集中的一个小批次的数据进行训练。
真随机梯度下降(SGD):每次抽取单一的一个样本进行训练。
批量随机梯度下降(BGD):每次选用全部的样本进行训练。
优化器时使用损失梯度更新参数的具体方式。
常见的优化器:带动量SGD、Adagrad、RMSProp等。
动量解决了SGD两个问题:收敛速度和局部最小点。
链式求导:反向传播算法
根据微积分的知识,可以通过“链式法则”对函数链求导:(f(g(x)))' = f'(g(x)) * g'(x)。
链式法则应用于神经网络梯度值得计算,得到得算法叫反向传播。
Tensorflow等框架可以进行符号微分,给定一个运算链,并且已知每个运算的导数,这些框架就可以利用链式法则来计算这个运算链的梯度函数。
将网络参数值映射为梯度值。而无需手动实现反向传播算法。


