HDU多校第一场 1007 Chiaki Sequence Revisited

1007. Chiaki Sequence Revisited

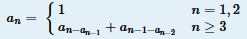
求 $\sum_{i=1}^{n}ai$ 。

打表发现差分数组为1,1,0,1,1,0,0,1,1,0...

即初始值为1，每次操作将数列的所有1变为1,1,0，所有0不变，迭代无穷多次，是分形结构。

现在已知差分序列，运用阿贝尔变换，即

$\sum_{i=m}^nf_k(g_{k+1}-g_k) =[f_{n+1}g_{n+1}-f_mg_m]-\sum_{k=m}^ng_{k+1}(f_{k+1}-f_k)$

可以将数组A与数组B的差分的乘积转换为数组B与数组A差分的乘积。

令原式中 $f_i=a_i$ , $g_i=i-2$ ，可得

$\sum_{k=1}^na_k =[a_{n+1}(n-1)+1]-\sum_{k=1}^ng_{k-1}(a_{k+1}-a_k)\\=(n-1)\sum_{k=0}^{n-2}(a_{k+3}-a_{k+2})-\sum_{k=0}^{n-2}(a_{k+3}-a_{k+2})k+1$

令 $da_k=a_{k+3}-a_{k+2}$ ，则

$\sum_{k=1}^na_i =(n-1)\sum_{k=0}^{n-2}da_i -\sum_{k=0}^{n-2}i\times da_i +1$

递归处理da即可。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 typedef long long LL;
 5 const int mod = 1e9 + 7;
 6 
 7 struct value_t
 8 {
 9     LL len, one, sum;
10     value_t() = default;
11     value_t(LL x, LL y, LL z): len(x), one(y), sum(z) {}
12 } dp[60];
13 
14 void prepare()
15 {
16     dp[0] = {3, 2, 1};
17     for (int i = 1; i < 60; ++i)
18     {
19         dp[i].len = dp[i - 1].len + dp[i - 1].one * 2;
20         assert(dp[i].len == dp[i - 1].len * 2 + 1);
21         dp[i].one = dp[i - 1].one * 2;
22         dp[i].sum = (dp[i - 1].sum * 2 + (dp[i - 1].len % mod) * (dp[i - 1].one % mod)) % mod;
23     }
24 }
25 
26 LL prefix, sum0, sum1;
27 
28 void update(LL len, LL one, LL sum)
29 {
30     sum0 += one;
31     sum1 += sum + (one % mod) * (prefix % mod) % mod;
32     prefix += len;
33     sum0 %= mod, sum1 %= mod;
34 }
35 
36 void solve(LL n, int depth, int trailing)
37 {
38     if (n == dp[depth].len + trailing)
39     {
40         update(n, dp[depth].one, dp[depth].sum);
41         return;
42     }
43     if (depth == 0)
44     {
45         if (n == 1)
46             update(1, 1, 0);
47         else
48             update(n, 2, 1);
49         return;
50     }
51     if (n <= dp[depth - 1].len)
52     {
53         solve(n, depth - 1, 0);
54     }
55     else
56     {
57         update(dp[depth - 1].len, dp[depth - 1].one, dp[depth - 1].sum);
58         solve(n - dp[depth - 1].len, depth - 1, trailing + 1);
59     }
60 }
61 
62 int main()
63 {
64     prepare();
65     int T;
66     for (scanf("%d", &T); T; T--)
67     {
68         LL n;
69         scanf("%lld", &n);
70         for (int i = 0; i < 60; ++i)
71             if (dp[i].len >= n)
72             {
73                 prefix = sum0 = sum1 = 0;
74                 solve(n, i, 0);
75                 printf("%lld\n", ((n - 1) % mod * (sum0 % mod) % mod - sum1 % mod + 1 + mod) % mod);
76                 break;
77             }
78     }
79 
80     return 0;
81 }

posted @ 2018-07-31 11:32 Aseer 阅读(147) 评论(0) 编辑收藏举报

刷新页面返回顶部

SUSTech TripleH

HDU多校第一场 1007 Chiaki Sequence Revisited

公告