PTA L3-023 计算图 (dfs+数学推导)
“计算图”(computational graph)是现代深度学习系统的基础执行引擎,提供了一种表示任意数学表达式的方法,例如用有向无环图表示的神经网络。 图中的节点表示基本操作或输入变量,边表示节点之间的中间值的依赖性。 例如,下图就是一个函数 ( 的计算图。
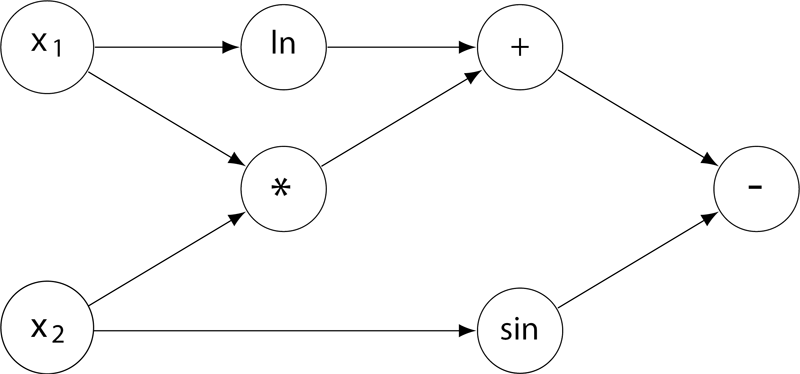
现在给定一个计算图,请你根据所有输入变量计算函数值及其偏导数(即梯度)。 例如,给定输入,,上述计算图获得函数值 (;并且根据微分链式法则,上图得到的梯度 ∇。
知道你已经把微积分忘了,所以这里只要求你处理几个简单的算子:加法、减法、乘法、指数(ex,即编程语言中的 exp(x) 函数)、对数(ln,即编程语言中的 log(x) 函数)和正弦函数(sin,即编程语言中的 sin(x) 函数)。
友情提醒:
- 常数的导数是 0;x 的导数是 1;ex 的导数还是 ex;ln 的导数是 1;sin 的导数是 cos。
- 回顾一下什么是偏导数:在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定。在上面的例子中,当我们对 x1 求偏导数 / 时,就将 x2 当成常数,所以得到 ln 的导数是 1,x1x2 的导数是 x2,sin 的导数是 0。
- 回顾一下链式法则:复合函数的导数是构成复合这有限个函数在相应点的导数的乘积,即若有 (,(,则 /。例如对 sin 求导,就得到 cos。
如果你注意观察,可以发现在计算图中,计算函数值是一个从左向右进行的计算,而计算偏导数则正好相反。
输入格式:
输入在第一行给出正整数 N(≤),为计算图中的顶点数。
以下 N 行,第 i 行给出第 i 个顶点的信息,其中 ,。第一个值是顶点的类型编号,分别为:
- 0 代表输入变量
- 1 代表加法,对应 x1+x2
- 2 代表减法,对应 x1−x2
- 3 代表乘法,对应 x1×x2
- 4 代表指数,对应 ex
- 5 代表对数,对应 ln
- 6 代表正弦函数,对应 sin
对于输入变量,后面会跟它的双精度浮点数值;对于单目算子,后面会跟它对应的单个变量的顶点编号(编号从 0 开始);对于双目算子,后面会跟它对应两个变量的顶点编号。
题目保证只有一个输出顶点(即没有出边的顶点,例如上图最右边的 -),且计算过程不会超过双精度浮点数的计算精度范围。
输出格式:
首先在第一行输出给定计算图的函数值。在第二行顺序输出函数对于每个变量的偏导数的值,其间以一个空格分隔,行首尾不得有多余空格。偏导数的输出顺序与输入变量的出现顺序相同。输出小数点后 3 位。
输入样例:
7
0 2.0
0 5.0
5 0
3 0 1
6 1
1 2 3
2 5 4
输出样例:
11.652
5.500 1.716
天梯赛L3的第二题,反向建图之后利用各种求导公式对每个变量分别跑一遍dfs求偏导就行了。场下30分钟过掉,场上的我真是宛如一个智障,~QAQ~
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 typedef double db; 5 const int N=5e4+10; 6 int n,f[N],dg[N],s,nxt[N][2],vis[N],x; 7 db a[N],f1[N],f2[N]; 8 vector<int> vec; 9 vector<db> ans; 10 void dfs(int u) { 11 if(vis[u])return; 12 vis[u]=1; 13 if(f[u]==0)f1[u]=a[u],f2[u]=u==x?1:0; 14 else if(f[u]==1) { 15 int v1=nxt[u][0],v2=nxt[u][1]; 16 dfs(v1),dfs(v2); 17 f1[u]=f1[v1]+f1[v2],f2[u]=f2[v1]+f2[v2]; 18 } else if(f[u]==2) { 19 int v1=nxt[u][0],v2=nxt[u][1]; 20 dfs(v1),dfs(v2); 21 f1[u]=f1[v1]-f1[v2],f2[u]=f2[v1]-f2[v2]; 22 } else if(f[u]==3) { 23 int v1=nxt[u][0],v2=nxt[u][1]; 24 dfs(v1),dfs(v2); 25 f1[u]=f1[v1]*f1[v2],f2[u]=f2[v1]*f1[v2]+f1[v1]*f2[v2]; 26 } else if(f[u]==4) { 27 int v=nxt[u][0]; 28 dfs(v),f1[u]=exp(f1[v]),f2[u]=exp(f1[v])*f2[v]; 29 } else if(f[u]==5) { 30 int v=nxt[u][0]; 31 dfs(v),f1[u]=log(f1[v]),f2[u]=f2[v]/f1[v]; 32 } else if(f[u]==6) { 33 int v=nxt[u][0]; 34 dfs(v),f1[u]=sin(f1[v]),f2[u]=cos(f1[v])*f2[v]; 35 } 36 } 37 int main() { 38 scanf("%d",&n); 39 for(int i=0; i<n; ++i) { 40 scanf("%d",&f[i]); 41 if(f[i]==0) { 42 scanf("%lf",&a[i]); 43 vec.push_back(i); 44 } else if(f[i]>=1&&f[i]<=3) { 45 int u,v; 46 scanf("%d%d",&u,&v); 47 nxt[i][0]=u,nxt[i][1]=v,dg[u]++,dg[v]++; 48 } else if(f[i]>=4&&f[i]<=6) { 49 int u; 50 scanf("%d",&u); 51 nxt[i][0]=u,dg[u]++; 52 } 53 } 54 for(int i=0; i<n; ++i)if(!dg[i])s=i; 55 for(int i:vec)x=i,memset(vis,0,sizeof vis),dfs(s),ans.push_back(f2[s]); 56 printf("%.3f\n",f1[s]); 57 for(int i=0; i<ans.size(); ++i)printf("%.3f%c",ans[i]," \n"[i==ans.size()-1]); 58 return 0; 59 }

