递归中的 DFS 与 DP 比较
一,递归
递归的过程我们可以认为是:一棵树的根节点向下搜索,并回溯的过程。 我们把根节点连接到所有通过递归延伸到的节点,该树即为递归树。
分支节点下面的第一条路径是通过调用递归函数延伸的,而该分支节点下的其它路径则是通过回溯延伸的。
二,超级楼梯的两种解法
1,题目
有一超级楼梯,共无限级。刚开始时你在地面,你可以一步跨上第一级,也可以一步跨上第二级。 假设你每次只能向上跨一级或二级,那么你要走上第N级,共有多少种走法?
2,DP 解法
将该问题分解为与前面几种状态的小问题,即到达第n个台阶的前一步,要么是从第n-1个台阶走上来的,要么是从n-2台阶走上来的,所以到达第n个台阶的走法就等于到达第n-1个台阶的走法加上到达第n-2个台阶的走法。则有:
递归函数:f(n) = f(n-1) + f(n-2)
函数出口:n == 1 的时候,f(n) = 1;n == 2 的时候,f(n) = 2

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #define N 50 int dp(int n) { if (n == 1) return 1; if (n == 2) return 2; return dp(n - 1) + dp(n - 2); } int main(void) { int n; while (scanf("%d", &n) != EOF) { printf("%d\n", dp(n)); } return 0; }
3,DFS 解法
这一题问的是有多少走法,那么我们除了用 dp 的方法,也可以利用 DFS 遍历每一种走法,然后用形参记录递归树的叶节点个数。
注意点:如果要保证某节点能够分支,那么该节点调用递归函数时,不能使用 return,因为 return 的话,直接返回上一层了,相当于截断该分支节点的所有分支。

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #define N 50 int dfs(int n, int &cnt) { if (n > 1) dfs(n - 2, cnt); if (n > 0) dfs(n - 1, cnt); if (n == 0) cnt = cnt + 1; return cnt; } int main(void) { int n; while (scanf("%d", &n) != EOF) { int cnt = 0; printf("%d\n", dfs(n, cnt)); } return 0; }
4,两者的递归树比较

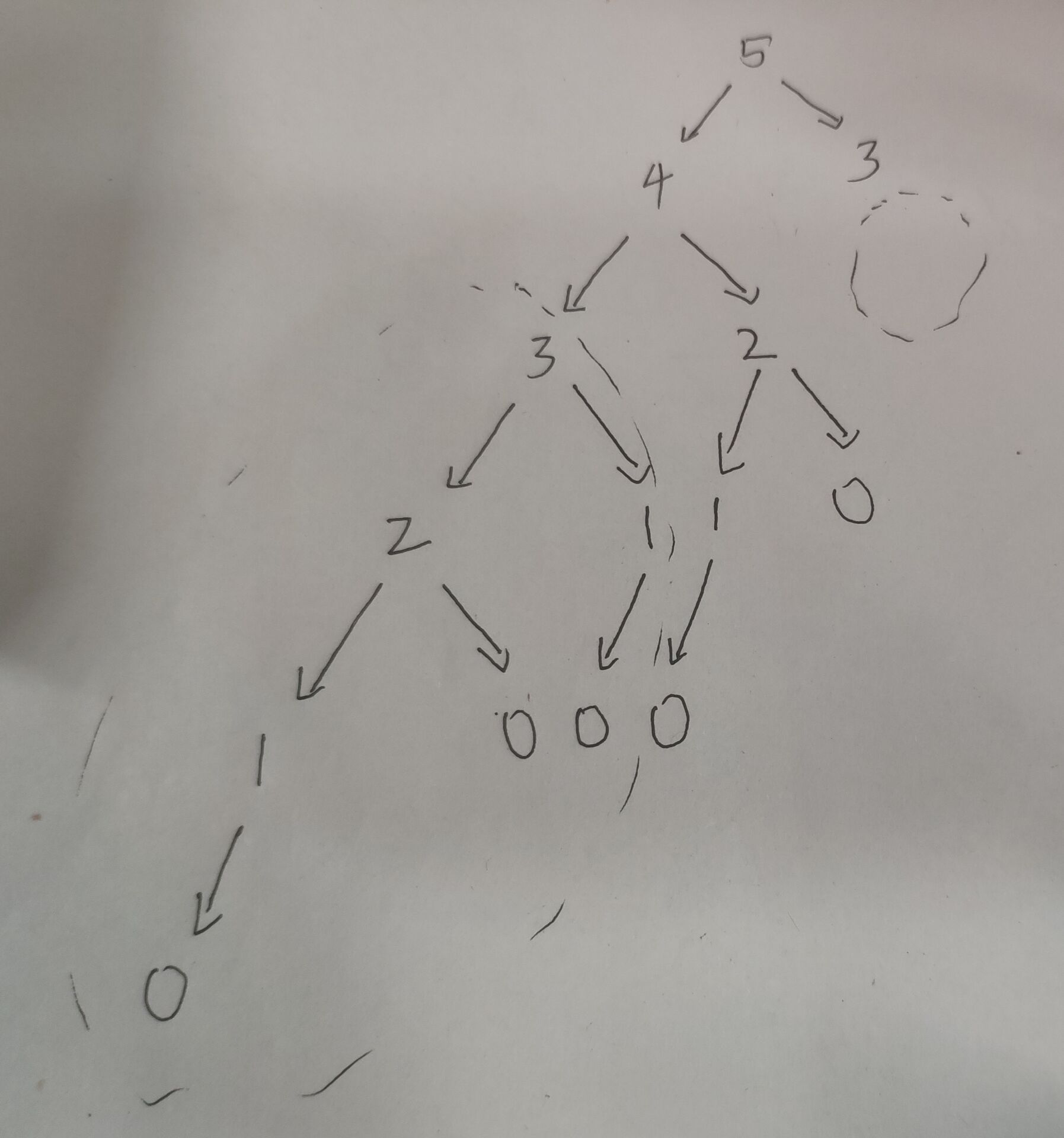
DP 的递归树的每个节点表示的是第n个台阶的走法次数。DFS 的递归树的每个节点表示的是当前走到第n个台阶。
DP 的递归树的每条边表示的是将当前状态分解为两个子状态。DFS 的递归树的每条边表示的是从当前台阶走到下一个台阶。
三,树塔问题的两种解法
1,问题
设有一个三角形的数塔,顶点为根结点,每个结点有一个整数值。从顶点出发,可以向左下走或向右下走,求最大的路径值。
2,DP 解法
将该问题分解为与前面几种状态的小问题,设 f(i, j) 为叶节点到达点ij 的路径最大值。则有
递归函数:
f(i, j) = max( fun(i+1, j), fun(i+1, j+1) ) + a[i][j]
递归出口:
if (j > i || i >= n) f(i, j) = 0
else return max( fun(i+1, j), fun(i+1, j+1) ) + a[i][j]

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #define N 20 int a[N][N]; int dp(int i, int j, int n) { if (i >= n || j > i) return 0; int b = dp(i + 1, j, n) + a[i][j]; int c = dp(i + 1, j + 1, n) + a[i][j]; return b > c ? b : c; } int main(void) { int n; scanf("%d", &n); for (int i = 0; i < n; i++) for (int j = 0; j <= i; j++) scanf("%d", &a[i][j]); printf("%d\n", dp(0, 0, n)); return 0; }
3,DFS 解法
这一题问的是有最大路径值,那么我们除了用 dp 的方法,也可以利用 DFS 遍历每一种走法,然后用形参记录递归每条路径的长度,保留当前路径值到形参max2,保留历史路径最大值到形参max1中。
注意点:形参max1用的是引用,每次遍历到叶节点更新;形参max2不用引用,这样回溯的时候就不用把手动减去回溯掉的路径值。

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #define N 20 int a[N][N]; int dfs(int i, int j, int n, int &max1, int max2) { if (j > i || i >= n) return 0; max2 += a[i][j]; dfs(i + 1, j, n, max1, max2); dfs(i + 1, j + 1, n, max1, max2); if (i == n - 1) max1 = max1 > max2 ? max1 : max2; return max1; } int main(void) { int n; scanf("%d", &n); for (int i = 0; i < n; i++) for (int j = 0; j <= i; j++) scanf("%d", &a[i][j]); int max1 = 0, max2 = 0; printf("%d\n", dfs(0, 0, n, max1, max2)); system("pause"); return 0; }
========== ======== ======== ======= ====== ===== ==== === == =
我的朋友,我还有一点疑虑——你是不是因为太懦弱了,才这样以炫耀自己的痛苦来作为自己的骄傲?
-- 《基督山伯爵》
My friend, I have a little doubt -- are you too weak to show off your pain as a source of pride?
-- ”The count of monte cristo“


