矩阵快速幂—— 构造矩阵
借鉴视频:https://www.bilibili.com/video/BV1gx41127d7?p=2
借鉴博客:https://blog.csdn.net/wangjian8006/article/details/7868864
一,汇总
矩阵乘法可以用来求递推式
基本形式:由一个 基础矩阵(用 A 表示) 和 递推矩阵(用 B 表示) 组成 (名字自己取的 ,也不知道有没有专业名称)
基础矩阵:由条件充分的已知元素组成,如 f(n-1) , f(n-2) 等等
递推矩阵:一个固定矩阵,元素不包含变量,基础矩阵 乘以 递推矩阵 可以得到 下一个基础矩阵
下一个基础矩阵:与基础矩阵大小相同,包含 f(n) 和 基础矩阵的一部分元素,下一个矩阵 乘以 递推矩阵可以得到 下下一个基础矩阵
下一个基础矩阵:与基础矩阵大小相同,包含 f(n) 和 上一个矩阵的一部分元素
注意:通常,如果 基础矩阵 只有一行,递推矩阵 是为方阵,其行数 为 基础矩阵的列数
二,Fibonacci
题目:斐波那契数列递推关系为:F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥2
这里有两种矩阵递推式,一个是题目给出的,一个可以自己推导出来。
1,这个是题目给出的这个推导式,我不会推导
 .
.
2,这个自己推导的递推式和第一个很像,不过还是有着本质区别,估计可以由这个推导出题目的递推式
推导过程:
由:Fn = Fn − 1 + Fn − 2 for n ≥2 可知,我们只需要两个元素,就有足够条件求下一个元素
所以:
基础矩阵由两个元素组成,f(1),f(0)
下一个矩阵也由两个元素组成:f(2),f(1)
由此,便可以求 递推矩阵:


#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 2 #define mod (int)1e4 int n; struct mat { int m[N][N]; }I; mat mul(mat a, mat b) { mat ret; memset(ret.m, 0, sizeof(ret.m)); for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { for (int k = 0; k < N; k++) ret.m[i][j] = (ret.m[i][j] + a.m[i][k] * b.m[k][j] % mod) % mod; } } return ret; } mat pow_mat(mat a, int n) { mat res = I; // 这个也可以换成 a,这样就不用在另外在乘一次了 while (n) { if (n & 1) res = mul(a, res); a = mul(a, a); n >>= 1; } return res; } void init() { for (int i = 0; i < N; i++) I.m[i][i] = 1; } int main(void) { init(); while (scanf("%d", &n) && n != -1) { if (n == 0) puts("0"); else if (n == 1) puts("1"); else // a 基础矩阵,b 递推矩阵 { mat b = { { { 1,1 }, { 1,0 } } }; mat a = { { 1,0 } }; b = pow_mat(b, n - 1); a = mul(a, b); // a 虽然是 1x2 矩阵,但是可以看成 除第一行以外元素 皆为 0 的 2x2 矩阵,所以可以用这个函数直接算 printf("%d\n", a.m[0][0]); } } system("pause"); return 0; }
三,Simple Problem
题目:If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .
Give you a0 ~a9,two integer k,m,outf(k)%m
递推过程:


#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 10 int n, mod; struct mat { int m[N][N]; }I; mat mul(mat a, mat b) { mat ret; memset(ret.m, 0, sizeof(ret.m)); for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { for (int k = 0; k < N; k++) ret.m[i][j] = (ret.m[i][j] + a.m[i][k] * b.m[k][j] % mod) % mod; } } return ret; } mat pow_mat(mat a, int n) { mat res = I; while (n) { if (n & 1) res = mul(a, res); a = mul(a, a); n >>= 1; } return res; } void init() { for (int i = 0; i < N; i++) I.m[i][i] = 1; } int main(void) { init(); while (scanf("%d%d", &n, &mod) != EOF) { mat a = { { 9,8,7,6,5,4,3,2,1,0 } }; mat b = { { { 0,1,0,0,0,0,0,0,0,0 }, { 0,0,1,0,0,0,0,0,0,0 }, { 0,0,0,1,0,0,0,0,0,0 }, { 0,0,0,0,1,0,0,0,0,0 }, { 0,0,0,0,0,1,0,0,0,0 }, { 0,0,0,0,0,0,1,0,0,0 }, { 0,0,0,0,0,0,0,1,0,0 }, { 0,0,0,0,0,0,0,0,1,0 }, { 0,0,0,0,0,0,0,0,0,1 }, { 0,0,0,0,0,0,0,0,0,0 } } }; for (int i = 0; i < N; i++) scanf("%d", &b.m[i][0]); if (n < 10) printf("%d", n%mod); else { b = pow_mat(b, n - 9); a = mul(a, b); printf("%d\n", a.m[0][0]); } } system("pause"); return 0; }
四,矩阵级数
题目:给出 一个 n × n 矩阵 A 和一个正整数 k, 求 S = A + A2 + A3 + … + Ak.
这一题我倒是想不出来,看的是文章开头提到的博主。
推导过程:先将 S 化为 S = A(I+A(I+A(I+...A(I+A)))) ( I 是单位矩阵)
假设 T 既是 基础矩阵 又是 推导矩阵,即 TxT 可以实现 A(A+I), 即 TxT 中要出现 A(A+I) 这个元素。
由因为 TxT 所以 T 是方阵,1x1 明显不可能,
那么便设 T 是 2x2,且 AA+AI 是 2x2 才比较可能出现的。
所以有:
易得,没有 AA+AI 这种形式,所以这个不行,那么接下来要怎么办呢?
讲真如果是我的话,是万万不可能想到 再乘一个 T,
虽然 T xT 没有AA+AI 这种形式,但是 TxTxT 却出现了
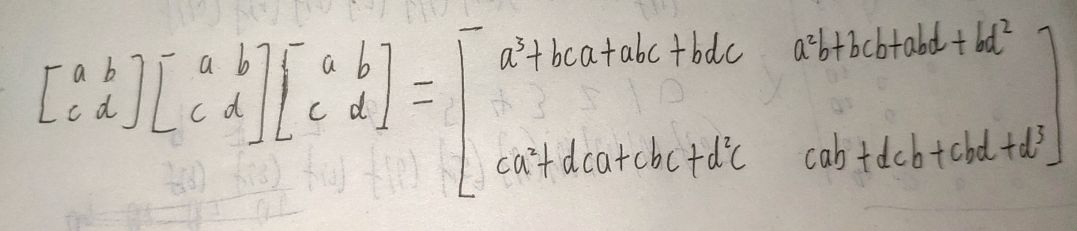
注意到 T[ 0 ][ 1 ] 出现了 aa和a , dd和d
T[ 1 ][ 0 ] 也同样出现了 aa和a , dd和d
这种形如 AA+AI 这种形式,
于是 我们可以将 T[ 0 ][ 1 ] 的 aa和a 看成 AA+A
于是 a = A, b = I ,d = I, 又因为 多了一个 bcd, 为了消除不必要计算和额外影响,
将 c = 0, 于是可得


#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 66 int n, k, m; struct mat { int m[N][N]; }A, I; mat mul(mat a, mat b) { mat ret; memset(ret.m, 0, sizeof(ret.m)); for (int i = 0; i < 2 * n; i++) { for (int j = 0; j < 2 * n; j++) { for (int k = 0; k < 2 * n; k++) ret.m[i][j] = (ret.m[i][j] + a.m[i][k] * b.m[k][j] % m) % m; } } return ret; } void init() { memset(I.m, 0, sizeof(I.m)); for (int i = 0; i < n * 2; i++) for (int j = 0; j < 2 * n; j++) if (i == j) I.m[i][j] = 1; } mat pow_mat(mat a, int n) { init(); while (n) { if (n & 1) I = mul(a, I); a = mul(a, a); n >>= 1; } return I; } void show() { for (int i = 0; i < n; i++) // 减去 一个单位矩阵 { for (int j = 0; j < n; j++) if (i != j) printf("%d ", A.m[i][j + n]); else { if (A.m[i][j + n] == 0) // %m 后变为 0,后减 1,变为 -1 printf("%d ", m - 1); else printf("%d ", A.m[i][j + n] - 1); } puts(""); } } int main(void) { scanf("%d%d%d", &n, &k, &m); memset(A.m, 0, sizeof(A.m)); for (int i = 0; i < n + n; i++) // 构造 递推矩阵 { if (i < n) for (int j = 0; j < n + n; j++) { if (j < n) scanf("%d", &A.m[i][j]); else if (i + n == j) A.m[i][j] = 1; } else for (int j = 0; j < n + n; j++) if (i == j) A.m[i][j] = 1; } A = pow_mat(A, k + 1); show(); system("pause"); return 0; }
五,由 Recursive sequence 改的
给出 f(1) 和 f(2) ,当 n>=3时有, f[n] = 2*f[n - 1] + 3*f[n - 2] + 3*n^5
这题的难点就在这个 n^5 的处理上,这个 n^5 是个变量 所以它要放在 基础矩阵 上,
但是他是会变的,我们要怎么实现这种变化呢,具体我们先看一下他要怎么变 (这里不看系数,因为系数是不变的,可以直接放在 递推矩阵里)

怎么由 3的5次方 得到 4的5次方 呢?估计有些人就会想到了,二项式定理。

于是可以推出,递推矩阵为:
2 1 0 0 0 0 0 0
3 0 0 0 0 0 0 0
3 0 1 0 0 0 0 0
15 0 5 1 0 0 0 0
30 0 10 4 1 0 0 0
30 0 10 6 3 1 0 0
15 0 5 4 3 2 1 0
3 0 1 1 1 1 1 1
且 A*B (n-2) 的第一个元素为 f(n)

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 8 #define ll long long ll n, aa, aaa; ll mod = 2147493647; struct mat { ll m[N][N]; void clear() { memset(m, 0, sizeof(m)); } }; mat mul(mat a, mat b) { mat ret; ret.clear(); for (int i = 0; i < N; i++) { for (int j = 0; j < N; j++) { for (int k = 0; k < N; k++) ret.m[i][j] = (ret.m[i][j] + a.m[i][k] * b.m[k][j]) % mod; /* 不要用这个,这个会超数据范围 int t = 0; for (int k = 0; k < N; k++) t += (a.m[i][k] * b.m[k][j]) % mod; ret.m[i][j] = t%mod;*/ } } return ret; } mat pow_mat(mat a, mat b, ll n) // // a * (b 的 n 次幂) { mat ret = a; while (n) { if (n & 1) ret = mul(ret, b); n >>= 1; b = mul(b, b); } return ret; } int main(void) { int t; scanf("%d", &t); while (t--) { scanf("%lld%lld%lld", &n, &aa, &aaa); if (n == 1ll) printf("%lld\n", aa); else if (n == 2ll) printf("%lld\n", aaa); else { mat a = { { aaa,aa,32,16,8,4,2,1 } }; mat b = { { { 2,1,0,0,0,0,0,0 }, { 3ll,0ll,0ll,0ll,0ll,0ll,0ll,0ll }, { 3ll,0ll,1ll,0ll,0ll,0ll,0ll,0ll }, { 15ll,0ll,5ll,1ll,0ll,0ll,0ll,0ll }, { 30ll,0ll,10ll,4ll,1ll,0ll,0ll,0ll }, { 30ll,0ll,10ll,6ll,3ll,1ll,0ll,0ll }, { 15ll,0ll,5ll,4ll,3ll,2ll,1ll,0ll }, { 3ll,0ll,1ll,1ll,1ll,1ll,1ll,1ll } } }; b = pow_mat(a, b, n - 2); printf("%lld\n", b.m[0][0] % mod); } } system("pause"); return 0; }
六,233 Matrix
题目:
233 Matrix TimeLimit:5000MS MemoryLimit:65536KB 64-bit integer IO format:%I64d Problem Description In our daily life we often use 233 to express our feelings. Actually, we may say 2333, 23333, or 233333 ... in the same meaning.
And here is the question: Suppose we have a matrix called 233 matrix. In the first line, it would be 233, 2333, 23333...
(it means a 0,1 = 233,a 0,2 = 2333,a 0,3 = 23333...) Besides, in 233 matrix, we got a i,j = a i-1,j +a i,j-1( i,j ≠ 0).
Now you have known a 1,0,a 2,0,...,a n,0, could you tell me a n,m in the 233 matrix? Input There are multiple test cases. Please process till EOF. For each case, the first line contains two postive integers n,m(n ≤ 10,m ≤ 10 9).
The second line contains n integers, a 1,0,a 2,0,...,a n,0(0 ≤ a i,0 < 2 31).
Output For each case, output a n,m mod 10000007. SampleInput 1 1 1 2 2 0 0 3 7 23 47 16 SampleOutput 234 2799 72937
这题主要难在题目没有给出基础矩阵,需要自己去寻找。
推导过程:
如图 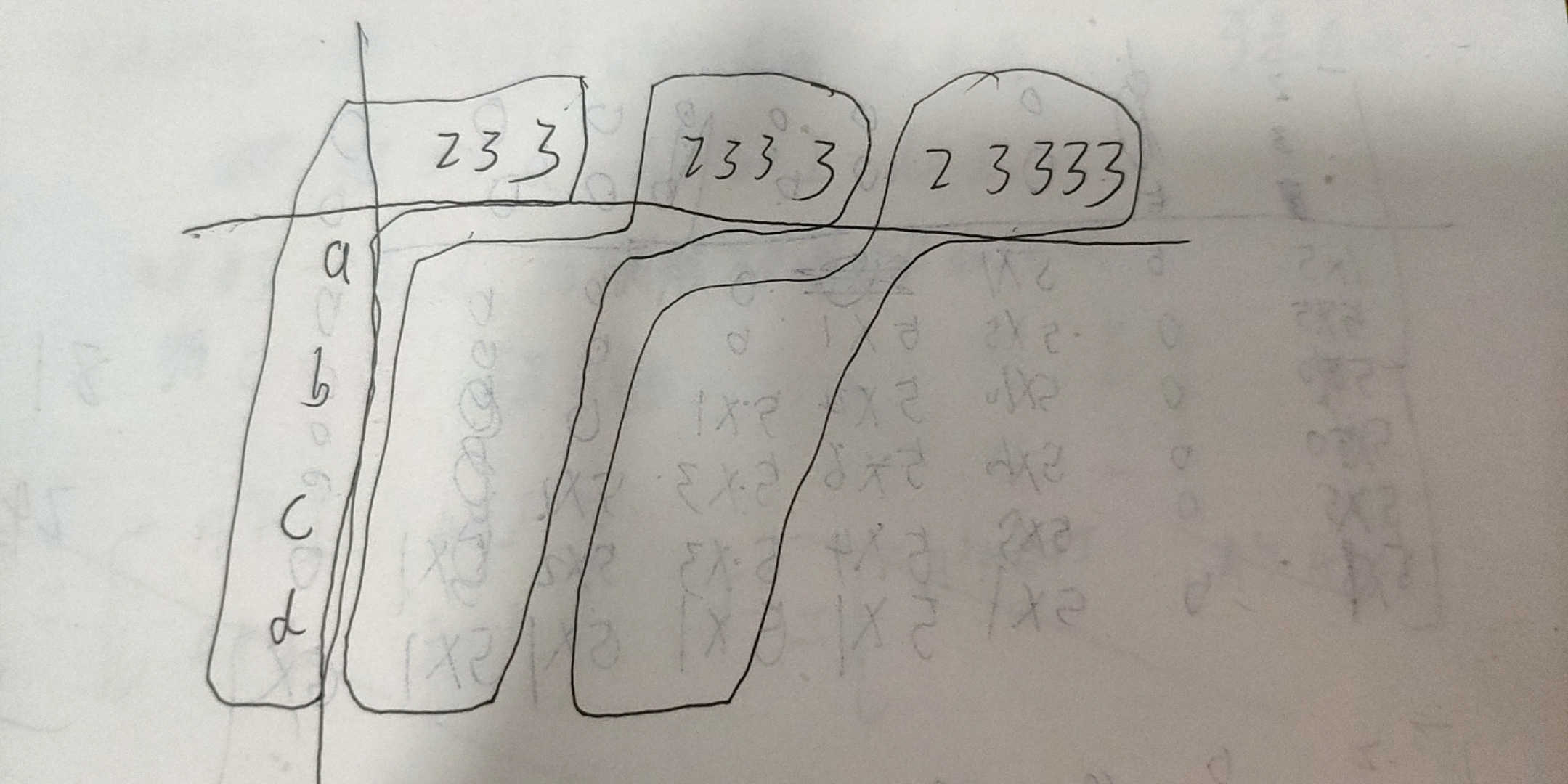
可以发现第二列未知元素 可以由第一列元素加上第二列第一个元素 推导出来
第三列未知元素 可以由第二列元素加上第三列第一个元素 推导出来
于是可知这里 每一列之间 存在递推关系,于是将 第一列加上第二列第一个元素 作为 基础矩阵,
于是有: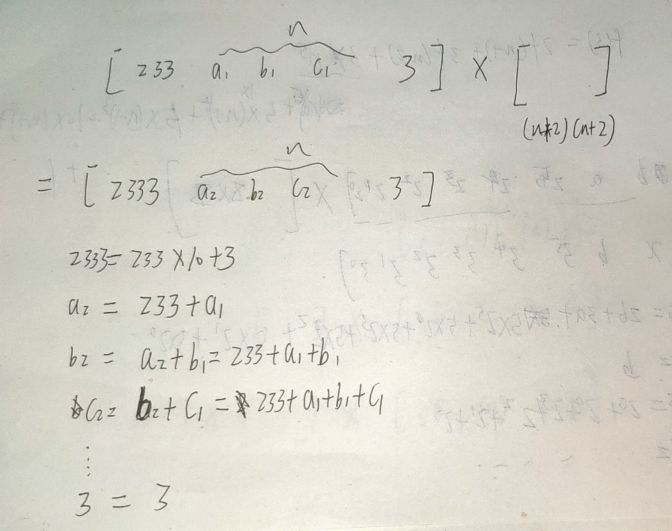
得到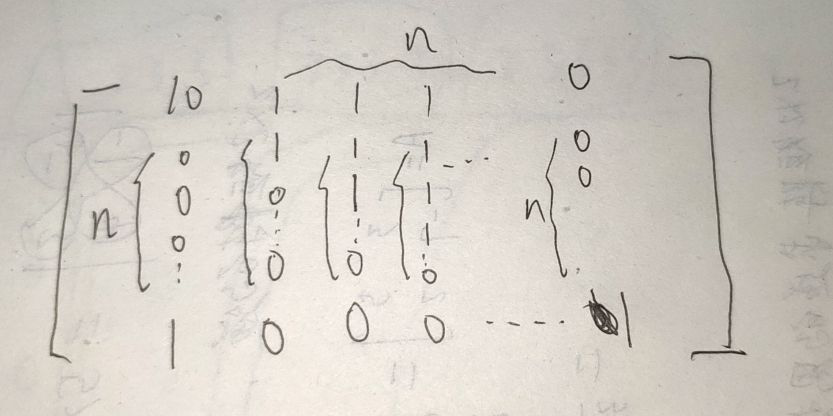

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define ll long long #define N 15 int n, m; int mod = 10000007; int t[N]; struct mat { ll m[N][N]; void clear() { memset(m, 0, sizeof(m)); } }; mat mul(mat a, mat b, int n) { mat ret; ret.clear(); for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { for (int k = 0; k < n; k++) ret.m[i][j] = (ret.m[i][j]%mod + a.m[i][k] * b.m[k][j]) % mod; } } return ret; } mat pow_mat(mat a, mat b, int n,int k) { mat ret = a; while (n) { if (n & 1) ret = mul(ret, b, k); n >>= 1; b = mul(b, b, k); } return ret; } int main(void) { while (scanf("%d%d", &n, &m) != EOF) { mat a, b; a.clear(); a.m[0][0] = 233, a.m[0][n + 1] = 3; for (int i = 1; i <= n; i++) scanf("%lld", &a.m[0][i]); b.clear(); b.m[0][0] = 10, b.m[n + 1][0] = 1; // 第一列 b.m[n + 1][n + 1] = 1; // 最后一列 for (int i = 1; i <= n; i++) // 中间 n 列 { for (int j = 0; j <= i; j++) b.m[j][i] = 1; } a = pow_mat(a, b, m, n+2); printf("%lld\n", a.m[0][n]); } system("pause"); return 0; }
=========== ========= ======== ====== ===== ==== === == =


