欧拉图的判定欧拉路的求法
其中 dfs 的代码 主要来自: https://blog.csdn.net/Jaster_wisdom/article/details/51067234
一,前言
这里讲的都是无向图,没讲有向的。
其中,如果 无向图没有奇数度结点,则具有欧拉回路,是欧拉图
如果 无向图有两个奇数度结点,则仅有欧拉通路,是半欧拉图
此外,则该无向图既不是欧拉图也不是半欧拉图
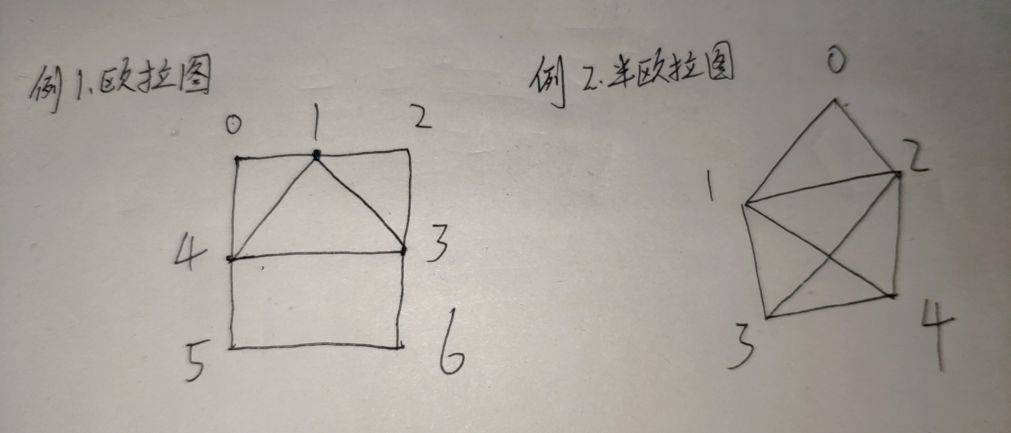
测试数据的图:
二,Fleury 算法
1, 算法思想
选取起点,其中欧拉图的起点任意,半欧拉图的起点从 两个奇度结点中的任意一个 开始。
然后从起点依次选边,每选一条边就从图中删去。选取条件是:① 与上一条已选取的边关联;② 除非无别的边可 选,否则不能选割边(桥)。
2,步骤
① 判断该图是什么图
② 选择起点
③ 删边
④ 将删除的边 加入 欧拉路中
⑤ 循环 ③ ④,直至 无边 可删
3,代码

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 1000 int a[N][N]; //邻接矩阵 int n, m; // n 点数 , m 边数 int judge_bridge(int i) // 通过判断以 i 为终点的边 是否 只有一个,来判断这条边是否是 割边 { int cnt = 0; for (int j = 0; j < n; j++) { if (a[i][j]) cnt++; } if (cnt == 1) return 0; return 1; } void Fleury(int cur) // cur 为起点 { int t = 0; // 记录割边的终点 int f3 = 0; // 标记 第一条边 while (1) { int f1 = 0; // 标记 是否有找到 正常边 int f2 = 0; // 如果有 割边,记录 第一条割边 for (int j = 0; j < n; j++) { if (a[cur][j]) { if (judge_bridge(j)) // 如果这条边不是割边,则删除这条边 { f1 = 1; a[cur][j] = 0; a[j][cur] = 0; printf(f3 == 0 ? "(%d,%d)" : "->(%d,%d)", cur, j); f3 = 1; cur = j; break; } if (judge_bridge(j) == 0 && f2 == 0) // 记录可能出现的割边,以备不时之需 { f2++; t = j; } } } if (f1 == 0 && f2 == 1) // 到了不选割边不行的地步了 { a[cur][t] = 0; a[t][cur] = 0; printf(f3 == 0 ? "(%d,%d)" : "->(%d,%d)", cur, t); f3 = 1; cur = t; } if (f1 == 0 && f2 == 0) // 无边可选,邻接矩阵空了,算法结束 { puts(""); break; } } } void creat() // 直接 输入邻接矩阵 { for (int i = 0; i < n; i++)//使用邻接矩阵表示图 { for (int j = 0; j < n; j++) { scanf("%d", &a[i][j]); } } } void judge() { int odd = 0; // 存奇数度数 的个数 int flag = 0; // 存 奇度边 的编号,如果是 半欧拉图 就从 奇度边 出发,若是 欧拉回路,就随便从 0 开始 for (int i = 0; i < n; i++) { int cnt = 0; for (int j = 0; j < n; j++) // 统计每个结点的 度数 cnt += a[i][j]; if (cnt % 2) // 若为 奇数,总数 +1 { flag = i; odd++; } } if (odd == 0) { printf("判定:该无向图没有奇数度结点,具有欧拉回路,是欧拉图\n"); printf("欧拉回路为:"); Fleury(flag); } else if (odd == 2) { printf("判定:该无向图有两个奇数度结点,仅有欧拉通路,是半欧拉图\n"); printf("欧拉通路为:"); Fleury(flag); } else printf("判定:该无向图既不是欧拉图也不是半欧拉图\n"); } int main(void) { while (scanf("%d", &n) != EOF) // 输入结点数 尝试了一下就 234 会有 欧拉路 { memset(a, 0, sizeof(a)); creat(); // 直接 输入邻接矩阵 judge(); // 判断 该 邻接矩阵 是什么图,若有欧拉路 则输出 路径 } system("pause"); return 0; } /* 测试数据1:欧拉回路 7 0 1 0 0 1 0 0 1 0 1 1 1 0 0 0 1 0 1 0 0 0 0 1 1 0 1 0 1 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 1 0 测试数据2:欧拉通路 5 0 1 1 0 0 1 0 1 1 1 1 1 0 1 1 0 1 1 0 1 0 1 1 1 0 */
三,DFS
1,个人感觉,不知对错
① 这里面虽然没有判断割边,但是判断了孤立点,它用深搜进行删边,这里的深搜只进行搜索删边,并没有回溯。
但是它将结点压入栈中了,然后再通过 栈中的结点 进行回溯,将孤立点加入通路中。那没什么存下来的路径不是散乱的点呢?
② 我们要明白一个前提就是这是个 欧拉图 或者是 半欧拉图,如果是从起点开始搜索的话,是有可能一次搜完的。
那什么时候会出现几条路径呢,只有它在有其他的路可选的情况下,搜索了割边。
③ 我猜测如果搜索的是割边的话,那么剩余图一定是回路(因为画了好几次都是这样,也不会证明,不知道对不对 ┌(; ̄◇ ̄)┘)
所以在我们通过 栈 里面的 结点 进行回溯时,在中间对剩余图进行再次深搜,就相当于在原通路中插入一条回路,仍然还是一条通路。
这样才能存下来的路径不是散乱的点
2,代码

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #include<stack> using namespace std; #define N 1000 int map[N][N], way[N]; stack<int>s; int n, m; // 点数 边数 void dfs(int k) { s.push(k); for (int i = 0; i < n; i++) // 一条路 删到没路 不管有无割边 { if (map[k][i]) { map[i][k] = map[k][i] = 0; dfs(i); break; } } } void Fleury(int k) { stack<int>ss; s = ss; // 栈的清空 int cnt = 0; s.push(k); // 起点入栈 while (s.size()) { int vertex = s.top(); s.pop(); int flag = 0; for (int i = 0; i < n; i++) // 通过判断 与vertx 相邻的边的个数 来判断是否 这点是否 是孤立点 { if (map[vertex][i] > 0) // 只要有边 就可以删 { flag = 1; break; } } if (flag == 0) // 该点是 孤立点 way[cnt++] = vertex; else // 不是孤立点 可以继续 删边 dfs(vertex); } for (int i = cnt - 1; i > 0; i--) // 打印路径 printf("%d->", way[i]); printf("%d\n", way[0]); } void judge() { int odd = 0; // 存奇数度数 的个数 int flag = 0; // 存 奇度边 的编号,如果是 半欧拉图 就从 奇度边 出发,若是 欧拉回路,就随便从 0 开始 for (int i = 0; i < n; i++) { int cnt = 0; for (int j = 0; j < n; j++) // 统计每个结点的 度数 cnt += map[i][j]; if (cnt % 2) // 若为 奇数,总数 +1 { flag = i; odd++; } } if (odd == 0) { printf("判定:该无向图没有奇数度结点,具有欧拉回路,是欧拉图\n"); printf("欧拉回路为:"); Fleury(flag); } else if (odd == 2) { printf("判定:该无向图有两个奇数度结点,仅有欧拉通路,是半欧拉图\n"); printf("欧拉通路为:"); Fleury(flag); } else printf("判定:该无向图既不是欧拉图也不是半欧拉图\n"); } int main(void) { scanf("%d%d", &n, &m); for (int i = 0; i < m; i++) { int x, y; scanf("%d%d", &x, &y); map[x][y] = map[y][x] = 1; } judge(); system("pause"); return 0; } /* 测试数据1:欧拉回路 7 10 0 1 0 4 1 2 1 4 1 3 2 3 3 4 4 5 5 6 6 3 测试数据2:欧拉通路 5 8 0 1 0 2 1 2 1 3 1 4 2 3 2 4 3 4 */
=========== ========= ======== ======= ====== ===== ==== === == =
哪里会有人喜欢孤独,只是不喜欢失望罢了。
—— 村上春树


