看正月点灯笼老师的笔记—线段树
视频地址:https://www.bilibili.com/video/BV1cb411t7AM?from=search&seid=10066884482637263864
代码
#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #define N 1000 int a[N] = { 1,3,5,7,9,11 }, tree[N]; void build_tree(int node, int start, int end) { //printf("%d %d\n", start, end); if (start == end) tree[node] = a[start]; else { int mid = (start + end) / 2; int left_node = 2 * node + 1; int right_node = 2 * node + 2; build_tree(left_node, start, mid); build_tree(right_node, mid + 1, end); tree[node] = tree[left_node] + tree[right_node]; } } void update_tree(int node, int start, int end,int id,int val) { //printf("%d %d\n", start, end); if (start == end) { a[id] = val; tree[node] = val; } else { int mid = (start + end) / 2; int left_node = 2 * node + 1; int right_node = 2 * node + 2; if (id >= start&&id <= mid) update_tree(left_node, start, mid, id, val); else update_tree(right_node, mid + 1, end, id, val); tree[node] = tree[left_node] + tree[right_node]; } } int query_tree(int node, int start, int end, int L, int R) { //printf("%d %d\n", start, end); if (start > R || end < L) // 剪枝 return 0; else if (L <= start&&R <= end) // 剪枝 return tree[node]; else if (start == end) return tree[node]; int mid = (start + end) / 2; int left_node = 2 * node + 1; int right_node = 2 * node + 2; int sum_left = query_tree(left_node, start, mid, L, R); int sum_right = query_tree(right_node, mid+1, end, L, R); return sum_left + sum_right; } int main(void) { build_tree(0, 0, 5); update_tree(0, 0, 5, 4, 6); for (int i = 0; i <= 14; i++) { printf("%d ", tree[i]); }puts(""); int sum= query_tree(0, 0, 5, 2, 5); printf("%d\n", sum); system("pause"); return 0; }
一,前引
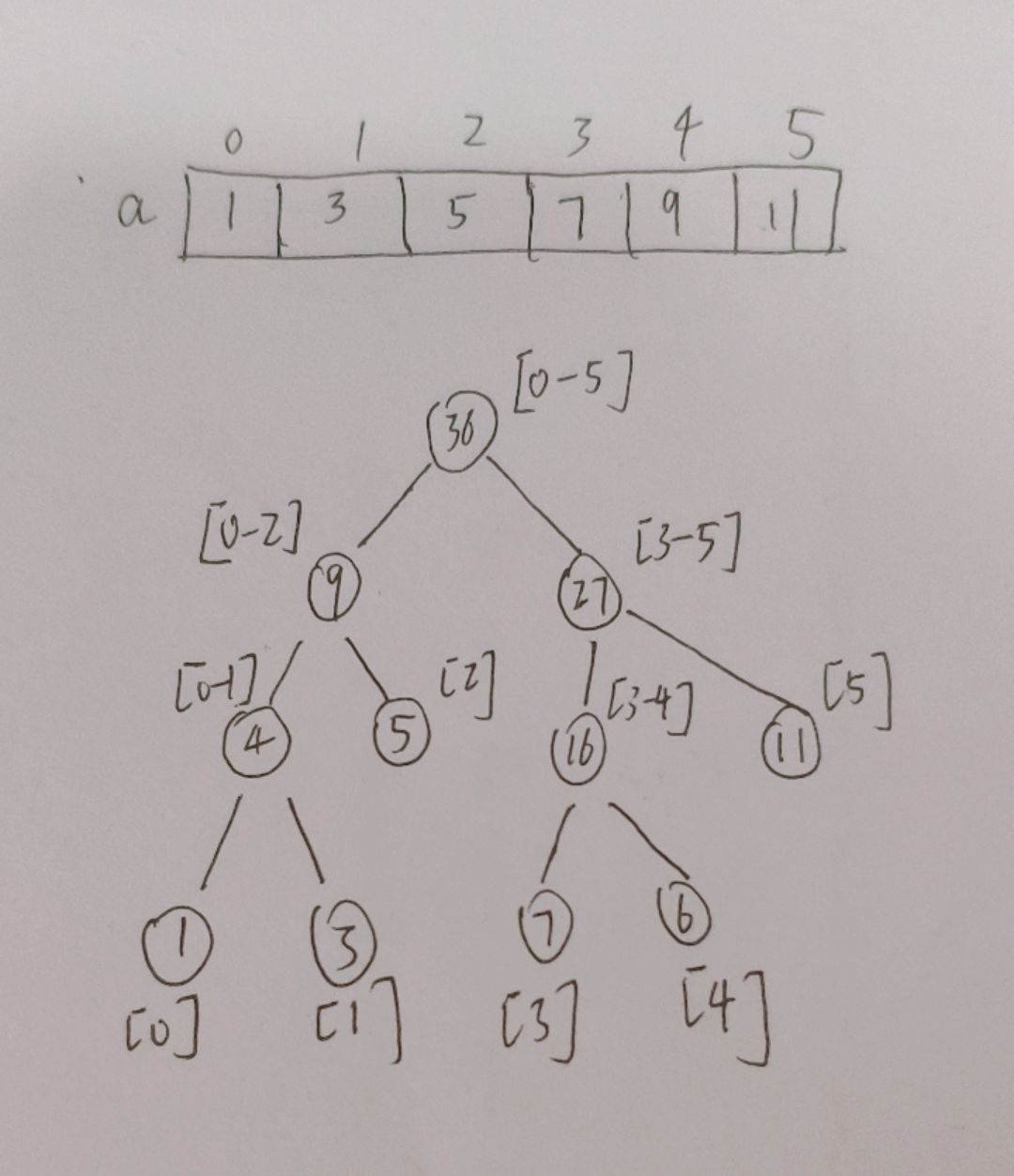

讲真,自己画一下有助于理解递归的过程。我就觉得画图的过程和递归过程可以说是一模一样。
这里的三个函数主要思想都是差不多的,只是后面多了 判断和剪枝。
二,build_tree 函数
体会一下画图的过程,我们不断把数组进行拆分成两个区间,直到区间只有一个元素时,这个结点的值就是这个元素的值。
然后再往上不断加回去,加到根节点。
这个就可以用递归实现,
我之前说过,可以将递归理解为 搜索和回溯 两部分
这里的搜索就是:不断把数组进行拆分成两个区间,直到区间只有一个元素时,这个结点的值就是这个元素的值
结束条件:区间只有一个元素时 即 start == end
这里的回溯就是:往上不断加回去,加到根节点
回溯发生在递归返回之后,所以我们只要在 递归函数 后面 求和就可以了
三,update_tree 函数
这个你也可以画一下图,你会发现,我们除了要 改变最后这个结点的值,在从根节点找到这个结点的路径上的所有结点的值也会受到影响
仍旧是递归
这里的搜索就是:不断把数组进行拆分成两个区间,判断这个区间内是否存在我们要改变的那个值,直到区间只有一个元素时,这个结点的值就是这个元素的值
结束条件:区间只有一个元素时 即 start == end
你会发现这个就只比第一个函数多了一个判断
这里的回溯就是:往上不断加回去,加到根节点
回溯发生在递归返回之后,所以我们只要在 递归函数 后面 求和就可以了
这里和第一个函数的区别是:由于这里在搜索时对路径进行了判断,所以回溯的路径只有一条路,而第一个函数是条条大路皆要回罗马 ╭(′▽`)╭(′▽`)╯
四,query_tree 函数
还是递归
没有剪枝之前:找到所有在 求和区间上的只代表一个元素的结点,累加求和
这里的搜索是:不断把数组进行拆分成两个区间,判断这个区间内是否存在我们要求和的区间,直到区间只有一个元素时,这个结点的值就是我们要求和的其中一个元素
结束条件:区间只有一个元素时 即 start == end
这里的回溯就是:往上不断加回去,加到根节点
由于我们已经判断了路径中 有没有我们要求的区间 ,所以,回溯求和时,
让有我们要求的区间,返回结点的值
没有我们要求的区间,返回 0
这样子就可以求和了
进一步优化:剪枝
由于我们在数组中已经记录了某一区间的和,
所以只要我们要查询的结点所代表的区间范围,在求和区间之内,可以直接返回这个节点的值,
不用搜索到区间只有一个元素。
over(●´∀`)♪
========= ======== ======= ======== ====== ===== ==== === == =
虞美人·听雨 蒋捷 宋
少年听雨歌楼上。红烛昏罗帐。
壮年听雨客舟中。江阔云低、断雁叫西风。
而今听雨僧庐下。鬓已星星也。
悲欢离合总无情。一任阶前、点滴到天明。

