并查集
参考:
https://www.bilibili.com/video/av38498175?p=1
借这个问题科普一下并查集各种情况下的时间复杂度 - 省份数量 - 力扣(LeetCode) (leetcode-cn.com)
一,并查集(Disjoint Set)概述
1,并查集的作用
① 检查图中是否存在环
2 ,并查集的流程
① 设定一个集合,叫并查集
② 往集合里面添加边,怎么添加呢?取边的起点和终点,判断两点是否都在集合里面。如果都在,则出现了环,如果不在,则将两个点放入集合中。
③ 继续添加下一条边,直到没有边。如果最后都没有找到环,就是图中不存在环。

二,并查集的构造
1, 在上述并查集的流程中,如果我们用集合表示并查集,自然也可以实现。但使用集合的话,在进行“集合合并”或者是“点是否属于该集合的判断”的话,时间复杂度应该是高于使用根数组(凭感觉,关于时间复杂度真的搞不懂)。
2, 并查集构造的三个动机:
能够表示点加入集合的不同状态;方便查找点是否存在于集合中;方便两个不同的集合进行合并。
3, 根数组(我不知道专业名称,这里暂时这样称呼)
为了满足上述三点,于是便有人想出了并查集算法,想出了用根数组:p 实现并查集。
p[i]:表示第i个点的父节点。
p 的初始化:p[i] = i; 或 p[i] = -1;
4, 表示点加入集合的不同状态
根数组用树的结构去表示点的状态。为什么用树呢?因为并查集算法就是为了检查环的存在,所以一旦有环的存在就会被判定为异常,即并查集无需表示环,而无环的连通图就是树。
有了数组p[i],就能根据父节点构造出森林出来,位于同一棵树的点自然属于同一集合。
5, 查找点是否存在于集合
并查集算法用根代表某一个集合。如果两个点的根一样,则表明两个点处于同一棵树上,即两个点同处于它们的根所代表的集合中。
而查找根的方法我们可以轻易根据数组p实现,只需要一层一层的用父节点往上循环,直到根节点。
那么,如何判断是否为根节点呢?因为根节点从未加入其他节点,所以根据初始化条件的不同,根节点的 p[i] = i; 或 p[i] = -1; 这就是初始化的目的。
6, 集合的合并
既然,我们根据树和根节点来作为集合的判断依据,那么,如果我们要合并集合a和集合b,其实就是合并树a和树b。所以我们只需要将树a的根指向树b的根,或者将树b的根指向树a就可以了。
7, 由于在合并集合的时候,我们对边的顺序是没有要求的。这种连接方式,并不能正确表示原来图的结构,只能表示点的连通关系。
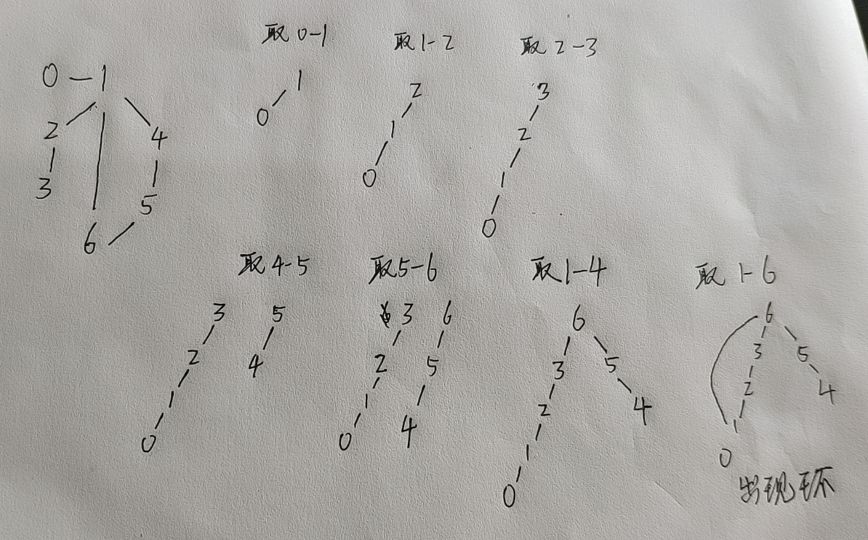
8, 代码

#define _CR_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 10 int p[N]; int find(int x) // 找到根节点 { int t = x; while (p[t] != -1) t = p[t]; return t; } int join(int x, int y) // 合并两个集合 { x = find(x), y = find(y); if (x == y) return 0; p[x] = y; return 1; } int main(void) { memset(p, -1, sizeof(p)); // 初始化 int edges[7][2] = { // 边集 {0,1},{1,2},{2,3},{4,5},{5,6},{1,4},{1,6} }; int f = 0; for (int i = 0; i < 7; i++) { int x = edges[i][0]; int y = edges[i][1]; if (join(x, y) == 0) { printf("存在环!\n"); f = 1; break; } } if (f == 0) printf("不存在环!\n"); system("pause"); return 0; }
三,按秩合并 与 路径压缩
1,目的:对上述算法中:“查找点的根”,这一步骤的时间复杂度的优化。
2,举例说明:
在集合合并的时候,在极端情况下会出现 0-1 1-2 2-3 3-4…… 这样一直让树的深度增加的情况。
这种情况就会导致点在查找根的时候,时间复杂度的增加。
3,所以,为了降低算法的时间复杂度,有人提出了压缩路径和按秩合并的思想。
4,按秩合并
① 秩:这里指树的深度。算法使用 rank 数组来记录树的深度,如 rank[x] = y 表示 以 x 点为根结点的树的深度为 y。
② 算法未开始时,此时所有的树只有一个点,没有边,所以每个点的深度为 0,所以rank数组初始化为全0
③ 算法开始合并时,比较要合并的两棵树的深度。
当两棵树的深度不一致时,让低的树的根指向高的树的根,这样新合并的树的高度就等于之前高的树的深度,而不会再度增加。
当两棵树的深度一致时,随便让一棵树的根指向另一棵树的根,这样新合并的树的高度就等于之前树的深度加上1,而不会增加很多。
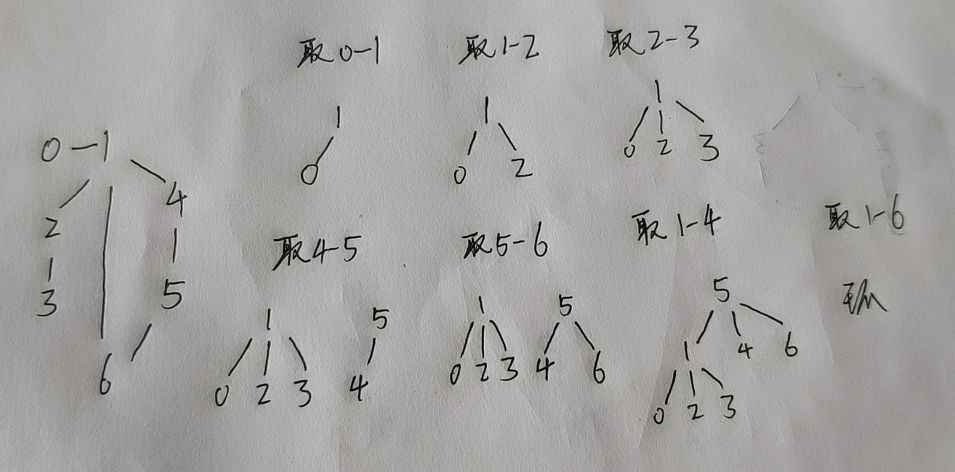
④ 代码

#define _CR_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 10 int p[N], rank[N]; int find(int x) // 找到根节点 { int r = x; while (p[r] != -1) r = p[r]; return r; } int join(int x, int y) // 合并两个集合 { x = find(x), y = find(y); if (x == y) return 0; if (rank[x] > rank[y]) // 让低的指向高的 p[y] = x; else if (rank[x] < rank[y]) p[x] = y; else { p[x] = y; rank[y]++; } return 1; } int main(void) { memset(p, -1, sizeof(p)); // 初始化 memset(rank, 0, sizeof(rank)); int edges[7][2] = { // 边集 { 0,1 },{ 1,2 },{ 2,3 },{ 4,5 },{ 5,6 },{ 1,4 },{ 1,6 } }; int f = 0; for (int i = 0; i < 7; i++) { int x = edges[i][0]; int y = edges[i][1]; if (join(x, y) == 0) { printf("存在环!\n"); f = 1; break; } } if (f == 0) printf("不存在环!\n"); system("pause"); return 0; }
5,压缩路径
① 直接在每一次查找某一点的根节点后,将该点到根节点的路径上的所有点指向根节点。
② 不过这种压缩路径存在一定的延迟,因为该压缩路径的代码是和查找写在一起的,即两个集合刚合并后,你并没有完成压缩路径,而是在查找时,才会去压缩路径。
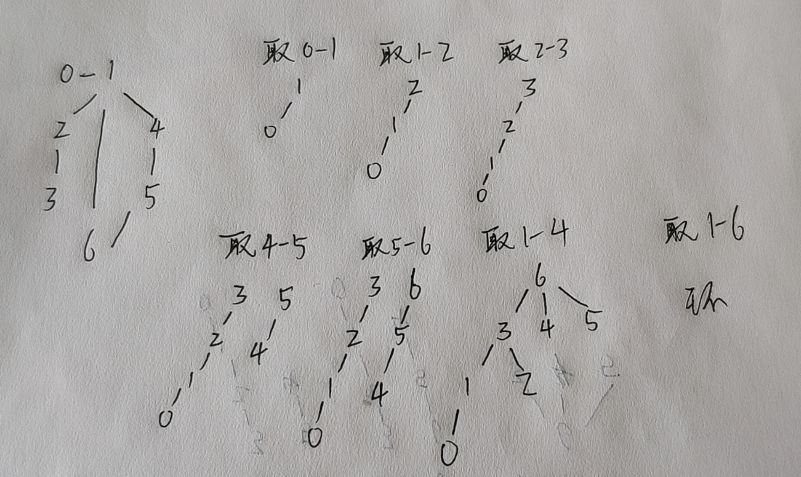
正如图中,刚开始并没有用到除了根节点的点,所以一直没有压缩路径。
一直到“取1-4”,此时点1和点4都不是根节点,所以在合并之前的查找,它会将点1到根节点路径上的点指向它的根节点3,将点4到根节点路径上的点指向它的根节点6。、
最后,压缩完路径的两个树在进行合并。
③ 代码

#define _CR_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 10 int p[N]; int find(int x) // 找到根节点 { int r = x; while (p[r] != -1) r = p[r]; while (x != r) { int t = p[x]; p[x] = r; x = t; } return x; } int join(int x, int y) // 合并两个集合 { x = find(x), y = find(y); if (x == y) return 0; p[x] = y; return 1; } int main(void) { memset(p, -1, sizeof(p)); // 初始化 int edges[7][2] = { // 边集 {0,1},{1,2},{2,3},{4,5},{5,6},{1,4},{1,6} }; int f = 0; for (int i = 0; i < 7; i++) { int x = edges[i][0]; int y = edges[i][1]; if (join(x, y) == 0) { printf("存在环!\n"); f = 1; break; } } if (f == 0) printf("不存在环!\n"); system("pause"); return 0; }

#define _CR_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 10 int p[N]; int find(int x) { if (p[x] != x) p[x] = find(p[x]); return p[x]; } int join(int x, int y) // 合并两个集合 { x = find(x), y = find(y); if (x == y) return 0; p[x] = y; return 1; } int main(void) { for (int i = 0; i < N; i++) // 初始化 p[i] = i; int edges[7][2] = { // 边集 { 0,1 },{ 1,2 },{ 2,3 },{ 4,5 },{ 5,6 },{ 1,4 },{ 1,6 } }; int f = 0; for (int i = 0; i < 7; i++) { int x = edges[i][0]; int y = edges[i][1]; if (join(x, y) == 0) { printf("存在环!\n"); f = 1; break; } } if (f == 0) printf("不存在环!\n"); system("pause"); return 0; }
其中,第二个代码是用递归实现 find函数,搜索时找根节点,回溯时压缩路径。
而且初始化为-1时,不能用递归实现,因为要指向根节点,如果初始化为自身则可以将返回值作为根节点,-1则不行。
四,按秩合并 + 路径压缩
1,只是简单的将两个函数放在一起,不用做什么特殊处理
2,明明压缩路径的时候,改变了树高,那么,为什么rank数组不需要维护?
答:不太清楚。应该是相对高度不变吧。
3,代码

#define _CR_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 10 int p[N], rank[N]; int find(int x) { if (p[x] != x) p[x] = find(p[x]); return p[x]; } int join(int x, int y) // 合并两个集合 { x = find(x), y = find(y); if (x == y) return 0; if (rank[x] > rank[y]) // 让低的指向高的 p[y] = x; else if (rank[x] < rank[y]) p[x] = y; else { p[x] = y; rank[y]++; } return 1; } int main(void) { for (int i = 0; i < N; i++) // 初始化 p[i] = i; memset(rank, 0, sizeof(rank)); int edges[7][2] = { // 边集 { 0,1 },{ 1,2 },{ 2,3 },{ 4,5 },{ 5,6 },{ 1,4 },{ 1,6 } }; int f = 0; for (int i = 0; i < 7; i++) { int x = edges[i][0]; int y = edges[i][1]; if (join(x, y) == 0) { printf("存在环!\n"); f = 1; break; } } if (f == 0) printf("不存在环!\n"); system("pause"); return 0; }
=========== ========= ========= ======= ====== ====== ===== === == =
菩萨蛮 其三 唐 韦庄
如今却忆江南乐,当时年少春衫薄。骑马倚斜楼,满楼红袖招。
翠屏金屈曲,醉入花丛宿。此度见花枝,白头誓不归。


