插入排序 和 希尔排序

参考：数据结构教程（第五版）李春葆主编

 

 

一，插入排序

1，算法思路（升序序列）

　　将数组分为有序区和无序区，初始时有序区只有a[0] (一个元素的话，自然有序)，剩下的都是无序区。然后从第二个元素依次往后，将每个元素插入有序区，共需插入 n-1 次。

　　插入的方法：从要插入的元素 key 的位置往前遍历，将每个大于 key 的元素后移一位

　　结束的条件/插入位置的判断：

　　　　遍历到第一个小于等于 key 的元素，则此时 key 要插入的位置就在该元素的后一位；

　　　　遍历结束后都没有找到小于等于 key 的元素，则此时 key 要插入的位置就在有序区的第一位

 

2，代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#define N 110
int a[N];
void insertSort(int n)
{
    // 从第二个元素依次往后，将每个元素插入有序区，共需插入 n-1 次
    for (int i = 1; i < n; i++)
    {
        // 找到要插入的位置，并将经过的元素后移
        int j = i, key = a[j];
        for (; j > 0 && a[j - 1] > key; j--)
            a[j] = a[j - 1];
        a[j] = key;
    }
}
int main(void)
{
    int n;
    while (scanf("%d", &n) != EOF)
    {
        for (int i = 0; i < n; i++)
            scanf("%d", &a[i]);

        insertSort(n);
        for (int i = 0; i < n; i++)
            printf("%d ", a[i]);
        puts("");
    }
    return 0;
}

 

3， 算法分析

① 时间复杂度

　　平均情况下：

　　　　对于每一次插入，都要将 a[t] 插入前面的有序区的 a[j] 的位置上。易得 1 <= t <= n-1，且 t 前面 0 ~t-1 个元素都是有序的，j 就是 t 要插入的位置。按平均概率来说，j 有 t+1 个位置可以选择，每个位置概率都是一样的，为 1/(t+1)。此时，需要将 j ~ t-1 范围内的元素全部后移，外加插入前的 key = a[t]，插入时的 a[t] = key，即移动次数为 t-j+2。还需要将 a[t] 与 j-1 ~ t-1 范围内的元素进行比较，即比较次数为 t-j+1 (当 j 为 0 时，比较次数为 t-j，该误差被忽略不计)。 所以有：

一次插入的平均时间复杂度为：

　　

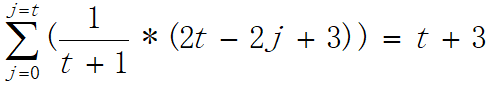
所以，总的时间复杂度为

　　

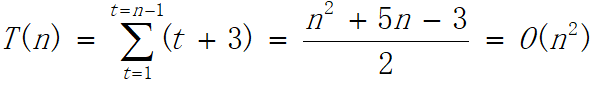
② 空间复杂度

　　插入排序算法中，只使用了 i，t，key 三个辅助变量，与问题规模 n 无关，所以时间复杂度为 O(1)。

③ 稳定性

　　如果有 a[i] = a[j]，且 i < j。那么插入排序是先将 a[i] 插入到有序区，再将 a[j] 插入到 a[i] 后面，则 a[i] 与 a[j] 的相对位置不变，所以插入排序是一种稳定的排序算法。

 

 

二，希尔排序

1，算法思路

　　希尔排序是一种分组插入排序。先对间隔大的子序列进行插入排序，再对间隔小的子序列进行插入排序。

 

2，代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#define N 110
int a[N];
void insertSort(int n, int gap) // 对间隔为 gap 的子序列进行插入排序
{
    for (int i = gap; i < n; i += gap)
    {
        int j = i, key = a[j];
        for (; j > 0 && a[j - gap] > key; j -= gap)
            a[j] = a[j - gap];
        a[j] = key;
    }
}
void shellSort(int n)
{
    // 间隔不断减少，直到间隔为 0 停止。(间隔为1的下一次)
    for (int gap = n / 2; gap; gap /= 2) 
        insertSort(n, gap);
}
int main(void)
{
    int n;
    while (scanf("%d", &n) != EOF)
    {
        for (int i = 0; i < n; i++)
            scanf("%d", &a[i]);

        shellSort(n);
        for (int i = 0; i < n; i++)
            printf("%d ", a[i]);
        puts("");
    }
    return 0;
}

 

3，算法分析

① 时间复杂度

　　因为间隔选取的不同，希尔排序的时间复杂度也是不一样的，且到目前为止最佳间隔的选取还是没有定论的。所以希尔排序算法的时间复杂度难以分析，不过一般认为是 O(n的1.3次方)。至于为什么希尔排序算法优于插入排序呢？

　　我们用定性的方法进行分析：

　　　　当 gap 值较大时：子序列中元素个数较少，插入次数较少，时间较快

   　　　当 gap 值较小时：子序列中元素个数变多，但数据已经基本有序，所以插入次数较少，时间还是较快

　　所以总体插入次数比较少。

② 空间复杂度

　　希尔排序算法中，只使用了 i，t，key，gap 四个辅助变量，与问题规模 n 无关，所以时间复杂度为 O(1)。

③ 稳定性

 　　希尔排序是一种不稳定的排序算法。

　　举例说明：

　　　　当数组 { 1, 3, 2, 2 } 以 gap=2 的间隔进行插入排序后，变成了 { 1, 2, 2, 3 } 。其中，原先下标为 2 的 2 位置不变，原先下标为 3 的 2 位置变为 1，跑到了下标为 2 的 2 前面，即两个 2 的相对位置发生了变化，说明希尔排序是一种不稳定的排序算法。

 

 

=========== ========= ======== ======= ====== ===== ==== === == =

When you treasure your past, are satisfied with your present, and are optimistic about your future,

you are on the top of your life.

When you understand that success will not make you, failure will not destroy you, flat will not drown you,

you stand on the highest point of life.