BFS(最小方案数)— 求 n 最少能表示成几个平方数的和

https://www.bilibili.com/video/av32546525 代码与思路来自此

 

题目是：求 n 最少能表示成几个平方数的和

由于有 1*1=1 这个数，所以问题一定有解，因为 1 可以组成所有正整数

 

其中视频用到了宽搜，我是一点也没想到这种方法。

①  把 0 作为起始点，0+一个平方数 作为下一层，0+一个平方数+一个平方数  作为再下一层，由此可组成一个树

 

②  然后标记距离 ， 0 距离为 0，0+一个平方数 距离为 1，0+一个平方数+一个平方数 距离为 2

 

③  所以 队列里面放的数为  0，0+一个平方数，0+一个平方数+一个平方数，这样循环结束的条件是 队列里 最先出现的那个 n

所以可以 是 那个取队首的变量 vertex == n

 

下面是我画的树：当 n == 13 时

 

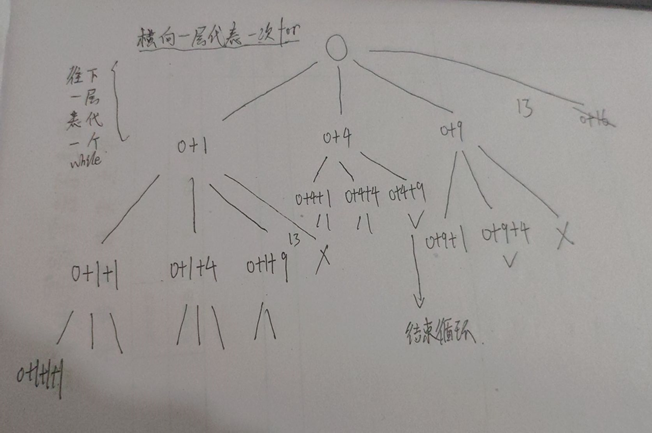
 下面是代码：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<vector>
#include<queue>
using namespace std;
int BFS(int n)
{
	queue<int>q;
	vector<int>dist(n + 1, INT_MAX);   // 考虑极端条件 平方数全部由 1 组成，且还需要储存下一层 所以需要 n+1
	q.push(0);
	dist[0] = 0;

	while (q.size() > 0)
	{
		int vertex = q.front();    // 结点
		q.pop();

		if (vertex == n)
			return dist[vertex];
		for (int i = 1; i*i + vertex <= n; i++)
		{
			int next = i*i + vertex;          // 下一个结点

			/* dist[i] 表示 i 最少可表示为几个数组成
			有几种情况：
			dist[next] <= dist[vertex] + 1： next 已经在这一步之前被标记好了，这就不用再放进队列里面了，因为这一步的距离一定不会比之前的更小
            dist[next] > dist[vertex] + 1：  next 还没被标记过，dist[next]=INT_MAX		*/
			if (dist[next] > dist[vertex] + 1)   
			{
				q.push(next);
				dist[next] = dist[vertex] + 1;
			}
		}
	}

}
int main(void)
{
	int n;
	while (scanf("%d", &n) != EOF)
	{
		printf("%d\n", BFS(n));
	}
	system("pause");
	return 0;
}

　　

 

=========== ========== ========= ======== ====== ===== ==== === == =

旅业书怀　　唐 杜甫

细草微风岸，危樯独夜舟。

星垂平野阔，月涌大江流。

名岂文章著，官因老病休。

飘飘何所似，天地一沙鸥。