串的模式匹配(BF + KMP + KMP 的优化)
参考:
https://www.bilibili.com/video/BV1Px411z7Yo?from=search&seid=7644406790653491226
https://baike.baidu.com/item/kmp%E7%AE%97%E6%B3%95/10951804?fromtitle=KMP&fromid=10158450&fr=aladdin
https://baike.baidu.com/item/BF%E7%AE%97%E6%B3%95/4326761?fr=aladdin
王道考研-数据结构
一,串的模式匹配
在主串中寻找一个给定的模式串,返回主串和模式串匹配的第一个子串的首字符位置
二,BF 算法
1,概要
BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法。
2,算法思想
将主串 text 的第一个字符与模式串 pattern 的第一个字符进行匹配,
若相等,则继续比较 text 的第二个字符和 pattern 的第二个字符;
若不相等,则比较 text 的第二个字符和 pattern 的第一个字符。
依次比较下去,直到得出最后的匹配结果。
3,代码
特点:存在主串剩余长度小于模式串的长度的剪枝判断

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 100 char text[N], pattern[N]; void BF() { // i 指向主串,j 指向模式串 int n = strlen(text), m = strlen(pattern); int cnt = 0; // 记录匹配成功的子串的个数 for (int k = 0; k <= n - m; k++) // k:记录 i 的起始位置 { int i = k, j = 0; while (i < n&&j < m) { if (text[i] != pattern[j]) break; i++, j++; } if (j == m) printf("找到了第 %d 个,起始位置在下标为 %d 位置\n", ++cnt, k); } } int main(void) { while (scanf("%s%s", text, pattern) != EOF) { BF(); } system("pause"); return 0; }
特点:格式等同于 KMP

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 110 char text[N], pattern[N]; void BF() { int n = strlen(text), m = strlen(pattern); int i = 0, j = 0, cnt = 0; while (i < n) { if (j == m - 1 && text[i] == pattern[j]) { printf("找到了第 %d 个,在 %d 的位置\n", ++cnt, i - j); i = i - j + 1, j = 0; } else if (text[i] == pattern[j]) i++, j++; else i = i - j + 1, j = 0; } } int main(void) { while (scanf("%s%s", text, pattern) != EOF) { BF(); } system("pause"); return 0; }
4,代码说明
① 用 k 记录主串的起始匹配位置,则 k <= n - m
证明:
因为要想模式串与主串匹配成功,则匹配的起始位置 + 模式串的长度 一定会小于等于主串的长度。
即 k + m <= n,所以 k <= n - m
② 第二种代码中,(j == m - 1 && text[i] == pattern[j]) 和 (text[i] == pattern[j]) 为什么是 if else 关系 ?
当一次完整匹配成功后,当 i 和 j 移动后,如果模式串只有一个字符,就相当于直接匹配到模式串最后一个,所以必须判断 j == m - 1,所以必须重头开始匹配
三,KMP 概述
1,概要
KMP 的起源:它是一种改进的字符串匹配算法,由 D.E.Knuth,J.H.Morris 和 V.R.Pratt 提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。
2,名词定义 (加粗的是自己为了方便创造的名词)
前缀:不包括最后一个字符的所有以第一字符开头的连续子串。
后缀:不包含第一个字符的所有以最后一个字符结尾的连续子串。
前后缀:前缀和后缀
最长公共前后缀:相同且最长的前后缀。
第 n 长公共前后缀:最长公共前后缀的最长公共前后缀的…(有 n 次这种嵌套关系)
主串:text[]
模式串:pattern[]
字符串 s 的前缀表:
prefix[i]:s 的前缀 s[0]~ s[i] 的最长公共前后缀的长度。因为数组下标是从零开始的,所以 prefix[i] 指向的是 s 的前缀 s[0]~ s[i] 的最长公共前后缀的前缀的最后一个字符的下一个字符处
某次匹配的起始位置:主串在以某个字符为起始位置与模式串匹配的过程中,这个某个字符的位置
部分成功前缀:主串在以某个字符为起始位置与模式串匹配的过程中,模式串中,直到匹配失败前的子串,即能够与主串成功匹配的那部分子串
失败子串:主串在以某个字符为起始位置与模式串匹配的过程中,主串中,直到匹配失败前的所有字符组成子串
部分成功后缀:部分成功前缀对应的主串中能够与之匹配的部分,且重中之重的来了,部分成功后缀是失败子串的后缀
3,最长公共前后缀
① 首先最长公共前后缀,不能包含自身。所以 prefix[ 0 ] = 0
② 虽然字符串 aba 是对称的,但是其最长公共前后缀为 a,而不是 ab。因为若其最长公共前后缀长度为 2 的话,则前缀为 ab,后缀为 ba,两者不同。
③ 字符串 s[0 ~ i-1] 的最长公共前后缀为 n 的话,字符串 s[0 ~ i] 最多只能为 n+1
反证法:
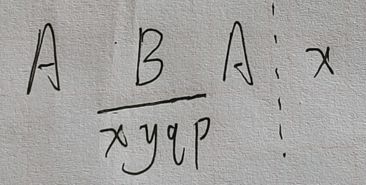
如图:已知 ABA 的最长公共前后缀为 A,B 由 x,y,p,q 组成,x 为已知字符,y,p 为未知字符,q 为未知字符串。接下来要计算 ABAx 的最长公共前后缀。
容易发现新增加的字符 x 与 B 的第一个字符 x 相同。于是最长公共前后缀由 A 变成 Ax。
而如果最长公共前后缀还想增加的话,只能比较 Axy 和 pAx 是否相同
假设两者相同,则有 Ax 和 pA 相同,则说明原先 ABA 的最长公共前后缀不是 A 而是 Ax,矛盾,假设不成立,命题得证。
四,KMP 函数
1,getPrefix 函数
① 函数功能:求模式串 pattern[] 的前缀表
③ 算法思想
如果 pattern[0~s] 有最长公共前后缀的话,那么一定是在 pattern[0~s-1] 的第 x 长公共前后缀的基础上加 1
③ 算法步骤
用 i 指向某一前缀,len 指向 pattern[0~i-1] 的第 x 长公共前后缀的前缀的最后一个字符的下一个字符处
用 i 循环 pattern 的每一个前缀
比较 pattern[i] 与 pattern[len]
如果相等:
说明 pattern[0~i] 的最长公共前后缀就是 pattern[0~len]
如果不相等 且 pattern[0~i-1] 还存在第 x+1 长公共前后缀:
则将 len 指向 pattern[0~i-1] 的第 x+1 长公共前后缀的前缀的最后一个字符的下一个字符处
如果不相等 且 pattern[0~i-1] 不存在第 x+1 长公共前后缀:
则说明 pattern[0~i] 不存在最长公共前后缀
2,move 函数
① 函数功能:将 prefix[] 里的值后移一位,第一位赋值为 -1,最后一位被覆盖掉
② 第一位赋值为 -1 目的:
prefix[0] 代表 pattern[j-1] 的所有第 x 长公共前后缀都与 text[i] 无法匹配不上的情况。
于是,我们可以在 prefix[j] == -1 时,判断出 text[i] 起始的所有子串都与 pattern 无法匹配,从而转去判断 text[i+1]。
③ 后移一位的目的
写代码比较方便。因为匹配失败后,需要的是最长公共前后缀的前缀的最后一个字符的下一个字符处,而不是最后一个字符的位置。
另外,prefix[0] 就没有意义了,我们可以将 prefix[0] 作为主串在以某个字符为起始位置与模式串匹配的过程中,匹配失败且部分成功后缀无法被再利用时的判断条件
3,KMP 函数
① 函数功能:利用 prefix[] 进行串的匹配
② 算法思想
所谓 KMP 算法,其本质就是在 BF暴力搜索的基础上,利用 prefix[],减少匹配失败后再次匹配的匹配次数。
③ 算法步骤
用 i 指向主串,j 指向模式串。
比较 text[i] 和 pattern[j]
如果相等
说明这一位匹配成功,i 指向主串的下一位,j 指向 pattern 的第一位
如果不相等
说明这一位匹配失败,i 不变,j 指向 prefix[j],即部分成功前缀的最长公共前后缀的前缀的最后一个字符的下一个字符处
如果 j == -1
说明,主串在以某个字符为起始位置与模式串匹配的过程中,匹配失败且部分成功前缀无法被再利用,则 i 指向主串的下一位,j 指向 pattern 的第一位
④ 算法证明
为什么 prefix[] 能减少匹配失败后,重新匹配的匹配次数呢 ?即匹配失败后为什么要 i 不变,j 指向 prefix[j] ?
证明:
设主串以第 x 个字符为起始位置与模式串匹配的过程中,在第 y 个字符匹配失败了。
有人发现,匹配失败后,如果按照 BF 将主串中的 i 指向 x+1 的位置,继续匹配且能够一直匹配到 y-1 的位置的话,匹配成功的部分不就是部分成功前/后缀的最长公共前后缀吗?
所以,我们只需要将 i 不变,j 指向 prefix[j],就等效于 BF 中
将主串中的 i 指向 x+1 的位置,j 指向模式串的第一位,继续匹配然后结果必然匹配失败,
将主串中的 i 指向 x+2 的位置,j 指向模式串的第一位,继续匹配然后结果必然匹配失败……
直到将 i 指向部分成功后缀的最长公共前后缀的后缀的起始位置,j 指向模式串的第一位, 继续匹配一直成功匹配到 i 指向 y,即部分成功后缀的下一位,此时 j 理所当然的指向部分成功前缀的最长公共前后缀的前缀的最后一个字符的下一位,即 j = prefix[j]
综上,就是 KMP 匹配失败的一步 j = prefix[j] 可以抵 BF 上述这么多次匹配。
为什么直到 i 移动到部分成功后缀的最长公共前后缀的后缀的起始位置,继续匹配然后结果必然匹配失败?
反证法:
设 i 移动到第 a 位,a 小于部分成功后缀的最长公共前后缀的后缀的起始位置,且 a 到部分成功后缀的最后一位都能与模式串匹配成功。
则此时匹配成功的部分是部分成功后缀的后缀与部分成功前缀的前缀,即部分成功后缀的公共前后缀。但是 a 还没有到达部分成功后缀的最长公共前后缀的后缀的起始位置,所以此时匹配成功的长度大于部分成功后缀的最长公共前后缀,即 部分成功后缀的最长公共前后缀不是最长公共前后缀,矛盾,命题成立
五,代码

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 110 char text[N], pattern[N]; int prefix[N]; void move(int m) // 后移前缀表 { for (int i = m - 1; i >= 0; i--) prefix[i + 1] = prefix[i]; prefix[0] = -1; } void getPrefix(int m) // 求前缀表 { prefix[0] = 0; // 只有一个字符没有前后缀 // i 指向前缀,len 指向前一个前缀的第 n 长公共前后缀的前缀的最后一个字符的下一个字符处 int i = 1, len = 0; while (i < m) { if (pattern[i] == pattern[len]) prefix[i++] = ++len; // len 是下标,与长度差 1,所以 len 先 ++ else if (len > 0) len = prefix[len - 1]; else prefix[i++] = len; // 此时 len == 0 } move(m); } void KMP() { int n = strlen(text), m = strlen(pattern); getPrefix(m); // 用 i 指向 text,j 指向 pattern int i = 0, j = 0, cnt = 0; while (i < n) { if (j == m - 1 && text[i] == pattern[j]) // j 移动到 pattern 的最后一位,并且这一位还与 text 匹配成功 { printf("找到了第 %d 个,起始位置在下标为 %d 的位置\n", ++cnt, i - j); j = prefix[j]; } else if (j == -1 || text[i] == pattern[j]) // 无法以 i 前面的位置作为起始位置 || 当前位匹配成功 i++, j++; else // 匹配失败 j = prefix[j]; } } int main(void) { while (scanf("%s%s", text, pattern) != EOF) { KMP(); puts(""); } system("pause"); return 0; } /* 测试样例 aaaaa a aaaaa aa aaaaa aaa abaabbaab abaa abaacababcac ababc */
注意:
① 前缀是不包括自己本身,但是在写代码时为了代码的完整性就顺带求了 prefix[n]。实际上这个值并没有用到,因为当模式串的最后一位字符与主串匹配成功的话就匹配结束了,而如果匹配不成功的话需要用到的值是 prefix[n-1]。
② 这里求得是主串中所有与模式串匹配的子串,所以 while 循环的条件是 i < n,如果只是求第一个匹配的子串,可以将 j < m 的条件加到 while 循环的条件上,并删除循环体中的 j == m - 1 的判断
③ 当一次完整模式匹配成功后,为什么只需要处理 j = prefix[j] ? 之后需要做什么?
答:当前位匹配失败和一次完整模式匹配成功后是等效的,需要执行 j = prefix[j],相当于执行了 BF 中的若干步。之后,主串的匹配的起始位置换了,但 i 和 j 已经指向了需要比较的字符,之后开始下一次的循环,继续匹配即可
④ 字符串下标从 0 开始和从 1 开始的区别?
两个的前缀表右移一位后都代表部分成功前缀的长度,区别在于:
从 0 开始的 prefix[j] 指向的就是 部分成功前缀的下一位;
从 1 开始的 prefix[j] 指向的是 部分成功前缀的最后一位
所以,从 1 开始的匹配失败后的移动是 j = prefix[j] + 1,于是,为了计算和写代码的方便,统一将从 1 开始的前缀表整体加 1。
于是,从 1 开始的匹配失败后的移动变成 j = prefix[j]
六,时间复杂度
BF 的时间复杂度为 O(mn)
KMP 的时间复杂度为 O(m + n)
七,KMP 的进一步优化
原理:当匹配失败后,i 不变,j 原先在 a 的位置,变成指向 b = prefix[j] 的位置。此时,若 pattern[a] = pattern[b] 相等,则此时的比较与之前的重复,没有意义。所以,可以将此时的 prefix[a] 修改为 prefix[b] 的值,直接跳过这一步重复的比较,指向下两步。
问题:这个优化的前提是匹配失败 pattern[j] 与 text[i] 不相等,它只针对匹配失败执行的 j = prefix[j] 的改进。若是一次完整的模式匹配后执行的 j = prefix[j],这样就默认下一步找到的 pattern[b] 也与 text[i] 不相等,这明显有问题。
解决办法:用两个 prefix 表,匹配失败用的优化后的,完整匹配成功用的是没有优化的
代码

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 110 char text[N], pattern[N]; int prefix[N]; // 没有优化的前缀表 int pval[N]; // 优化的前缀表 void moveAndOpt(int m) // 后移前缀表并且优化前缀表 { for (int i = m - 1; i >= 0; i--) prefix[i + 1] = prefix[i]; prefix[0] = -1; pval[0] = -1; for (int i = 1; i < m; i++) if (pattern[i] == pattern[prefix[i]]) pval[i] = prefix[prefix[i]]; else pval[i] = prefix[i]; } void getPrefix(int m) { prefix[0] = 0; int i = 1, len = 0; while (i < m) { if (pattern[i] == pattern[len]) prefix[i++] = ++len; else if (len > 0) len = prefix[len - 1]; else prefix[i++] = len; } moveAndOpt(m); } void KMP() { int n = strlen(text), m = strlen(pattern); getPrefix(m); int i = 0, j = 0, cnt = 0; while (i < n) { if (j == m - 1 && text[i] == pattern[j]) { printf("找到了第 %d 个,起始位置在下标为 %d 的位置\n", ++cnt, i - j); j = prefix[j]; } else if (j == -1 || text[i] == pattern[j]) i++, j++; else j = pval[j]; } } int main(void) { while (scanf("%s%s", text, pattern) != EOF) { KMP(); puts(""); } system("pause"); return 0; } /* 测试样例 aaaaa a aaaaa aa aaaaa aaa abaabbaab abaa abaacababcac ababc */
=========== ========= ======= ======= ====== ===== ==== === == =


