NOI2008 假面舞会 DFS
首先分析了一下之后,可以得到两种情况:
1.整个图无环。此时的最大值是每个连通块内最长链的和,最小值是3(注意最少面具数是3,不满足直接输出-1 -1)
2.图中有环。这里的环分为很多种:一种是首尾相连形成的环,,一种是奇奇怪怪的环例如1->2->3->4->5->6,7->6,7->8,1->8。
我们尝试从任意一个点开始dfs并标号,如果存在一条a->b的边,则a的类型为k,b的类型为k+1(同余关系下)。
同时为了从任意点开始都遍历到所有点,对每一条边都建一条长度为-1的反向边。
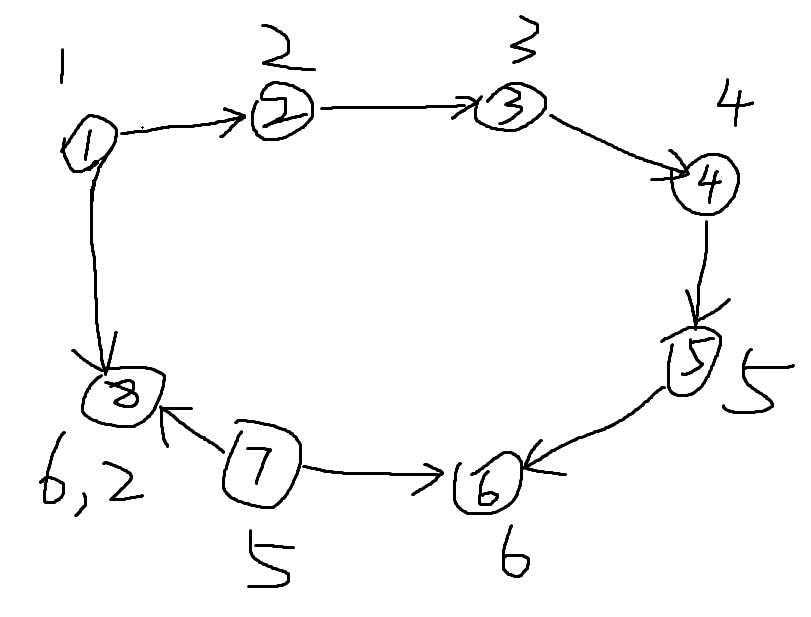
例如下图,当dfs两次经过一个点时,就能判断找到了环。
此时8的编号既可以是6又可以是2,说明6和2模k同余。这样就得到了满足这个环的k,同时它的因数也满足这个环的条件。
对每个环的k求gcd就是最大种类,最小种类就是>=3的因数。
using namespace std;
const int MAXN = 100500;
const int MAXM = 1000500;
int fir[MAXN], nxt[MAXM << 1], to[MAXM << 1], len[MAXM << 1], cnt;
int dfn[MAXN], vis[MAXN];
inline int read(){
int k = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){k = k*10 + ch - '0'; ch = getchar();}
return k * f;
}
inline void add_edge(int a, int b, int l){
len[cnt] = l; to[cnt] = b;
nxt[cnt] = fir[a]; fir[a] = cnt++;
}
int gcd(int a, int b){
if(b == 0) return a;
return gcd(b, a % b);
}
int maxx, minn, Gcd;
void dfs(int u, int num){
// printf("u = %d, num = %d\n", u, num);
if(vis[u]){
int tmp = abs(num - dfn[u]);
// printf("tmp = %d\n", tmp);
if(tmp){
if(!Gcd){
Gcd = tmp;
}
else{
Gcd = gcd(Gcd, tmp);
}
}
return;
}
dfn[u] = num; vis[u] = true;
maxx = max(maxx, num);
minn = min(minn, num);
for(int i = fir[u]; i != -1; i = nxt[i]){
int v = to[i];
dfs(v, num + len[i]);
}
}
int main(){
memset(fir, -1, sizeof(fir));
int n = read(), m = read();
for(int i = 1; i <= m; i++){
int a = read(), b = read();
add_edge(a, b, 1);
add_edge(b, a, -1);
}
int ans1 = 0;
for(int i = 1; i <= n; i++){
if(!vis[i]){
maxx = -1e9, minn = 1e9;
dfs(i, 1);
ans1 += maxx - minn + 1;
}
}
if(Gcd){
if(Gcd < 3){
printf("-1 -1");
}
else{
for(int i = 3; i <= Gcd / 2; i++){
if(Gcd % i == 0){
printf("%d %d", Gcd, i);
return 0;
}
}
printf("%d %d", Gcd, Gcd);
return 0;
}
}
else{
if(ans1 < 3){
printf("-1 -1");
}
else{
printf("%d 3", ans1);
}
}
return 0;
}```

