PID自动(反馈)控制
1 自动(反馈)控制
1.1 概述
自动控制(automatic control)是指在没有人直接参与的情况下,利用外加的设备或装置,使机器、设备或生产过程的某个工作状态或参数自动地按照预定的规律运行。
1.2 来源与原始形态
自动化控制技术的广泛应用则开始于欧洲的工业革命时期。瓦特在发明蒸汽机的同时,应用反馈原理,于1788年发明了离心式调速器。当负载或蒸汽量供给发生变化时,离心式调速器能够自动调节进气阀的开度,从而控制蒸汽机的转速。
1.3 例子
空调温控,车速控制。
2 PID控制
2.1 闭环自动控制技术的基础
当今的闭环自动控制技术都是基于反馈的概念以减少不确定性。
2.2 反馈理论的要素:测量、比较和执行
测量关键的是被控变量的实际值,与期望值相比较,用这个偏差来纠正系统的响应,执行调节控制。
2.3 PID控制
在工程实际中,应用最为广泛的调节器控制规律为比例(proportion)、积分(integral)、微分(derivative)控制,简称PID控制,又称PID调节。
在闭环系统的控制中,可自动对控制系统进行准确且迅速的校正。PID算法已经有100多年历史,在四轴飞行器,平衡小车、汽车定速巡航、温度控制器等场景均有应用。
2.3.1 PID控制原理
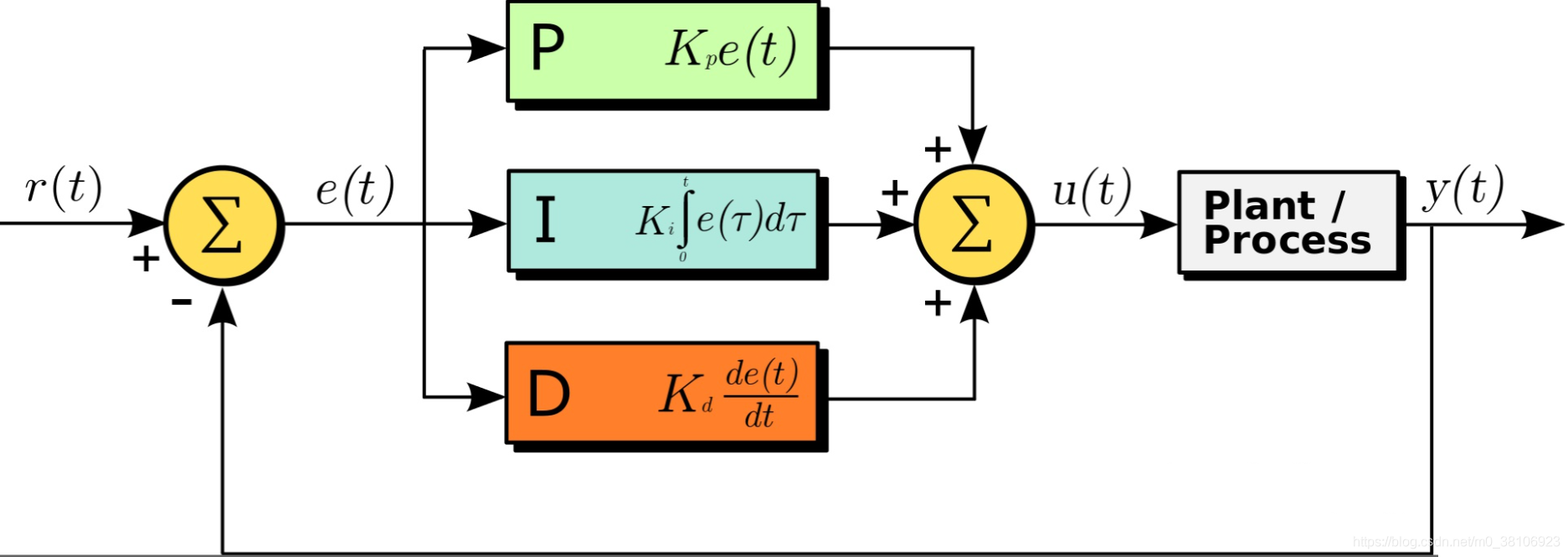
r(t):所需的设定值、目标值;
y(t):测量的过程输出值、实际值;eg.每0.1s得到的车轮速度。
e(t):偏差是设定值(目标值)与过程值(实际值)的差(r(t)-y(t));通过反馈慢慢使之为0。
u(t):经过计算得到的控制变量,输入到控制器中。
$u(t)=K_p·e(t)+K_d×\frac{e(t)-e(t-1)}{\delta t}$
P : proportion(非负比例系数),就是偏差乘以一个常数。
I : integral(非负积分系数),就是对偏差进行积分运算。
D : derivative(非负微分系数),对偏差进行微分运算。
eg.控制小车:将小车速度设定值r(t)为3m/s,由光电码盘测得速度为3.2m/s,即过程输出值y(t);偏差e(t)为-0.2m/s。
P:将-0.2m/s乘以一个系数(正)输入到控制器中,以减小输出的占空比,则车轮转速将降低,向设定值靠近。KP越大则调节的灵敏度越大,但过大可能会使实际速度低于3m/s(超调)。
I:只经过比例调节的小车,可能稳定后的速度为3.1m/s,存在稳态误差-0.1m/s;虽然误差很小,但是因为积分项也会随着时间的增加而加大,它推动控制器的输出增大,从而使稳态误差进一步减小,直到等于0。
D:小车中有些组件存在较大惯性或者滞后性,其变化总是落后于误差的变化。假设经比例调节后实际速度为3.1m/s,则设定速度与实际速度的差值由-0.2m/s变为-0.1m/s,e(t)的差分为0.1m/s2,将此差分乘以系数(正)加到控制变量中,相比只有比例环节减缓了速度降低的趋势(减小超调量)。
|
调整方式 |
上升时间 |
超调量 |
安定时间 |
稳态误差 |
稳定性 |
|
↑ Kp |
减少 ↓ |
增加 ↑ |
小幅增加 ↗ |
减少 ↓ |
变差 ↓ |
|
↑ Ki |
小幅减少 ↘ |
增加↑ |
增加 ↑ |
大幅减少↓↓ |
变差↓ |
|
↑ Kd |
小幅减少 ↘ |
减少↓ |
减少↓ |
变动不大→ |
变好 ↑ |
上表是独立增加参数的影响
2.3.2 PID数学表达
$u(t)=K_pe(t)+K_d\frac{de(t)}{dt}+K_i\int_t^0e(t')dt'$
$K_p,K_i,K_d$都是非负的,先$K_p$(比例项,调整效果最大),再$K_d$(微分项),最后$K_i$(积分项,消除误差)
2.3.1 PID参数整定
1.PID参数调整特点
难点不是编程,而是控制器的参数整定。
输入r(t)为阶跃响应。下图为不同参数下的输出y(t)响应。
理想:稳定、振高少、收敛快
① $K_p$增加,$K_i$ 、$K_d$不变
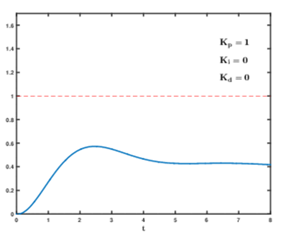
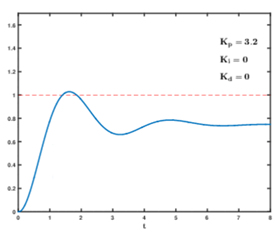

②$K_p$不变,$K_i$ 增加(少量增加),$K_d$不变


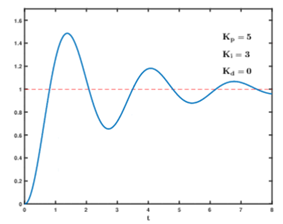
③$K_p$、$K_i$不变,$K_d$增加

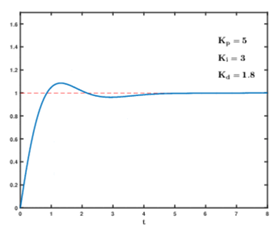

PID系统输出影响:
(1)增大比例系数 使系统反应灵敏,调节速度加快,并且可以减小稳态误差。
但比例系数过大会使超调量增大,振荡次数增加,调节时间加长,动态性能变坏,比例系数太大甚至会使闭环系统不稳定。
(2)增大微分系数 可以减小超调量和稳定时间。
(3)增大积分系数 会减小稳态误差,但会增大超调量和稳定时间。
2.3.4 离散型PID
在计算机上进行PID调节时只能用离散型PID。
假设采样间隔为T,则在第kT时刻:
偏差$e(k) = r(k) - y(k)$
积分环节用加和的形式表示,即$e(k) + e(k-1) + …$
差分环节用斜率的形式表示,即$e(k) - e(k-1)$
从而有位置式PID :
$u(k)=K_pe(k)+K_d\frac{e(k)-e(k-1)}{\delta t}+K_i·\sum_{j=1}^k e(j)$
由两次的u(k)相减可以得到增量式PID:
$\delta u(k) = u(k) - u(k-1)=K_p[e(k)-e(k-1)]+K_Ie(k)+K_D[e(k)-2e(k-1)+e(k-2)]$
(1)增大比例系数 使系统反应灵敏,调节速度加快,并且可以减小稳态误差。
但是比例系数过大会使超调量增大,振荡次数增加,调节时间加长,动态性能变坏,比例系数太大甚至会使闭环系统不稳定。
(2)增大微分系数 可以减小超调量和稳定时间。
(3)增大积分系数 会减小稳态误差,但会增大超调量和稳定时间。
PID中三个参数,大体对应于控制系统的三个最重要的方面:
P对应“稳”,即稳定性,放大控制作用;I对应“准”,消除稳态误差;D对应“快”,对误差进行预判、做出快速反应。
3 用控制器使一锅水的温度保持在50℃
1. Kp比例增益
Kp比例控制考虑当前误差,误差值和一个正值的常数Kp(表示比例)相乘。需要控制的量,比如水温,有它现在的当前值,也有我们期望的目标值。
① 当两者差距不大时,就让加热器“轻轻地”加热。
② 要是因为某些原因,温度降低了很多,就让加热器“稍稍用力”加热。
③ 要是当前温度比目标温度低得多,就让加热器“开足马力”加热,尽快让水温到达目标附近。
Kp越大,调节作用越激进,Kp调小会让调节作用更保守。
2. Kd微分增益
Kd微分控制考虑将来误差,计算误差的一阶导,并和一个正值的常数Kd相乘。
当比较接近目标时,P的控制作用就比较小了,越接近目标,P的作用越小。当有很多内在的或者外部的因素,使控制量发生小范围的摆动。由于P在接近目标时的作用小,整个系统不是特别稳定,总是在“抖动”,因此需要一个控制作用,让被控制的物理量的“变化速度”趋于0,即类似于“阻尼”的作用。
D的作用就是让物理量的速度趋于0,只要什么时候,这个量具有了速度,D就向相反的方向用力,尽力刹住这个变化。Kd参数越大,抑制能力就越强。
3. Ki积分增益
Ki积分控制考虑过去误差,将误差值过去一段时间和(误差和)乘以一个正值的常数Ki。设置一个积分量,只要偏差存在,就不断地对偏差进行积分(累加),并反应在调节力度上。
即使与目标值相差不是太大,但是随着时间的推移,只要没达到目标,这个积分量就不断增加。到了目标温度后,假设没有波动,积分值就不会再变动。
Ki的值越大,积分时乘的系数就越大,积分效果越明显,所以,I的作用就是,减小静态情况下的误差,让受控物理量尽可能接近目标值。
4 【走直线的问题】
小车差分驱动(左、右轮分别用电机驱动,通过改变两个电机的转速实现小车前进和转向)仍是主流。
两个电机驱动有差异且不可能完全相同,导致两个轮子转速不同,就使得小车本该直线行驶的轨迹发生偏移。
运转过程中的扰动,如轮子瞬间打滑、有微小的障碍物等因素,都会导致左右轮不同速,从而“走偏”。
5 闭环控制
来源:学会PID-基于板球平衡系统-初中基础就能听懂的简单讲_哔哩哔哩_bilibili 日期:2023/07/27

比例P
偏差量 = 目标量 - 小球位置
比例P = 偏差量 * 比例P系数
执行量 = 比例P
比例P的效果:距离目标量差距越大,把其拉回目标值的力量就越大
比例P的缺点:1.数值固定 2.不辩情形 3.单一时间点
比例P过小可由增幅器(积分I)补充,比例P过大可由抑制器(微分D)补充
积分I
增幅器(积分I)->利用过去累加经验,判断比例P是否需要帮助,从而增加数值
积分I = 积分I + 偏差量 * 积分I系数
①限制幅度
如果积分I>最大值,则令积分I=最大值
如果积分I<最小值,则令积分I=最小值
②不运行时清零
执行量 = 比例P + 积分I
微分D
抑制器(微分D)->预测未来,即用当前偏差量减去上一次偏差量就可能是下一次偏差量
再用下一次偏差量提前参与到计算中,防止P过大产出超出目标的问题
微分D = (偏差量 - 上一次偏差量) * 微分D系数执行量 = 比例P + 积分I + 微分D
上一次偏差量 = 偏差量
伪代码
#计时 运行时间 = (系统运行时间()- 计时)/1000 计时 = 系统运行时间() #PID部分 for n in range(0,2): 偏差量[n] = 目标量[n] - 小球位置[n] 比例P[n] = 偏差量[n] * 比例系数P[n] 积分I[n] = 积分I[n] + 偏差量[n] * 积分I系数[n] * 运行时间 if 积分I[n]>积分I最大值[n]: 积分I[n] = 积分I最大值[n] elif 积分I[n]<- 积分I最大值[n]: 积分I[n]=-积分I最大值[n] 微分D[n] = (偏差量[n] - 上一次偏差量[n]) * 微分D系数[n]/运行时间 上一次偏差量[n] = 偏差量[n] 执行量[n] = 比例P[n] + 积分I[n] + 微分D[n] #控制平台倾斜 控制平台(执行量)
【注】1.板球平衡需要x轴和y轴独立调节,故需要两套PID
(用for循环让PID运行2次,其中每个变量均由两个元素列表组成,可完成两组PID计算)
积分I与微分D通过时间维度获得,故其与时间息息相关——程序执行速度固定则无需考虑此问题,但程序执行速度会变,则应该考虑时间问题
因为经历了更长时间,所以积分I需要乘时间系数,而微分D预测未来则相反,即除时间系数。
闭环控制和PID的过程
1.设置目标量
2.通过传感器结果获得偏差量
3.偏差量输入PID输出执行量
4.执行量给执行器从而可以纠正执行器,从而达到想达到的效果
5.PID核心是比例P,积分I是增幅器,微分D是抑制器
PID调参的顺序和关联
①比例P:基础运行能力。太小不能达到目标,太大则会超出目标。
②积分I:补足P过小的问题,对小偏差量起作用。太小会使小偏差量无法回正,不能到目标。太大会使系统表现迟钝,导致超出目标。
③微分D:阻止超出目标。太小会超出目标,太大会对误差敏感,导致被调节对象在目标范围附近高频抖动。
调整的例子
假设画面宽度是240,其中舵机角度是50,其中50/240=0.2
step1 调P,计算偏差量和执行量的比例
step2 调D,能限制超出目标。有足够的限制力后,就可以增加P;每个周期小球移动50,抬高5:5/50=0.1。但实测0.1偏大了,所以调小
step3 调I,可以加快回正,解决小偏差。同时也可以减小P
无人机悬停的例子
来源:通俗易懂的 PID 控制算法讲解_哔哩哔哩_bilibili
目的:控制无人机悬停高度
可控部分:无人机螺旋桨的旋转速度(速度越快,螺旋桨产生的升力越大)
开环控制很难使无人机飞行到指定高度,因为无人机受到重力、空气扰动和阻力等各种不确定因素

将误差进行比例放大,微分阻尼,积分误差补偿
PID作为闭环控制单元实现了三个目的:
P是实现当前误差闭环控制,
I是实现过去一段时间Tn内的累积误差控制,
D则是对未来某个时间段Tv内的预测累积误差控制。
所以PID三个增益参数都是对时间状态的预测。
step1 设无人机安装了传感器,可以感知当前飞行高度
→可计算“当前高度”到“目标高度”的误差
→误差值越大,给无人机提供的升力就越大
【$F = 0.01 × error = K_p × error$】
$K_p$越大,升力和误差的比例越大,控制系统响应速度更快,但无人机接近目标高度时振荡更严重
step2 为解决系统震荡,通过微分,计算速度$v=\frac{d(error)}{dt}$→D算法可对无人机速度做出响应
无人机速度过快→D算法抵消一部分P算法计算得到的升力→减缓系统震荡
$K_d$从0.01增大至0.05,无人机震荡明显改善,再增大到比如0.1则会失控!!!所有参数不能被设置的过大!
要找到平衡点,防止过冲。(PID的每一个值被设置的过大都会产生不同的震荡效果,通常在信号处理中会用"过冲"来描述这个现象。)
btw, 工程上说微分默认就是差分
step3 无论如何调整$K_p$或$K_I$值,误差永远不会被消除为0
因为误差存在→无人机升力存在→无人机接近目标高度时,升力和重力会平衡→无人机不再继续上升
故需要累积误差值,让长期误差值得不到修正的无人机有更大的升力,迫使无人机上升
I会对误差累积,提供更大的升力。加入$K_I$让无人机慢慢朝目标高度靠拢,让误差消除为0
I每一次控制循环都会逐渐累加,但是累加的值是根据当前测量的“误差”决定的。如果当前误差逐渐趋于0,那么I就不再累加,逐渐趋于一个固定值。
这个时候整个系统达到稳定,I并不会无止境的一直累加上去的(比如在视频中的例子中,I的这部分会提供一个额外的向上的力,使得无人机能够攀爬到达指定的高度)
事实上,I除了会累“加”也会累“减”,这取决于当前测量的“误差值”的“正负”。
在线模拟程序: https://rossning92.github.io/pid-simulation

算法伪代码
previous_error := 0 integral := 0 loop: error := setpoint - measured_value integral := integral + error × dt derivative := (error - previous_error) / dt output := Kp × error + Ki × integral + Kd × derivative previous_error := error wait(dt) goto loop
开源PID库
1.Python https://github.com/m-lundberg/simple-pid
2.C https://github.com/saxbophone/pid
3.Javascript https://github.com/Philmod/node-pid-controller
4.Java https://github.com/tekdemo/MiniPID-ava

【Arduino 101】五分钟搞懂PID控制算法_哔哩哔哩_bilibili
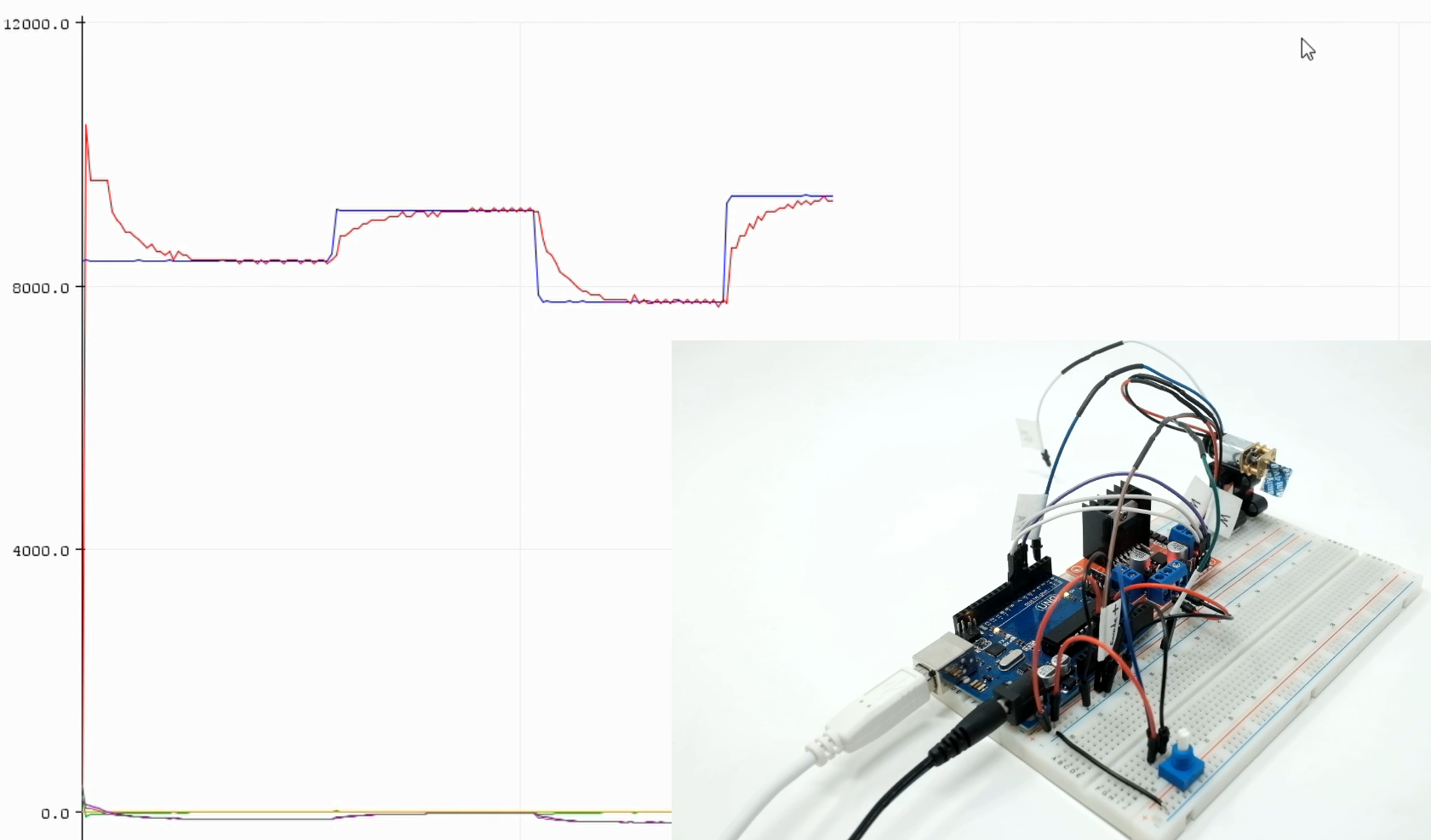
6 PID分类及温度调节实例
来源:假如不调PID,小车会“魔怔”吗?一个例程整明白PID的意义_哔哩哔哩_bilibili
位置式PID
$u(t) = K_p[e(t) + \frac{1}{T_i}\int_0^te(t)dt + T_d\frac{de(t)}{dt}]$
离散位置PID
$u_k = K_p[e_k + \frac{T}{T_i}\sum_{j=0}^k e_j + T_d \frac{e_k-e_{k-1}}{T}]$
$K_p$控制器比例系数
$T_i$控制器积分时间,$\frac{K_p}{T_i}$积分系数
$T_d$控制器微分时间,$K_p · T_d$微分系数
比例调节(P)
- 成比例的反映控制系统的偏差信号。
- 偏差一旦产生,控制器立即产生控制作用,以减少偏差。
- 通常随着值的加大,闭环系统的超调量加大,系统响应速度加快;但是当增加到一定程度,系统会变得不稳定。
积分调节(I)
- 积分控制器不断积累系统误差,输出控制量,直至无差。
- 强弱取决于积分时间常数T,越小,积分作用就越强。
- 积分作用太强会使系统超调加大,甚至使系统出现振荡。
微分调节(D)
- 微分控制可以减小超调量,克服振荡,提高系统稳定性。
- 加快系统的动态响应速度,减小调整时间,从而改善系统的动态性能。
【舵机采用的】位置式PID优缺点
优点:1.非递推式算法可直接控制执行机构
2.在执行机构不带积分部件的对象中可以很好应用
缺点:1.每次输出均与过去的状态有关
2.计算时要对e(k)进行累加,运算工作量大
【电机采用的】增量式PID优缺点
优点:1.误动作时影响小,必要时可以通过逻辑判断的方法去掉出错数据
2.手动自动切换的冲击小,便于实现无扰动切换(计算机出现故障或单片机出现数据扰动时,PID仍能保持原值)
3.算式中不需要累加
缺点:积分截断效应大,有稳态误差
PID变式
位置式PID
增量式PID
串接式PID
积分分离式PID
ADRC
其他
基于Arduino的自动空调温度测试器
- 实际生活中,需要在一天中的不同时间将空调的设定温度改变成不同的值,以始终保持舒适的环境。
- 测试器使用温度传感器(DHT11)读取房间的当前温度。
- 通过一个类似于空调遥控器的红外发射器向空调发送PID运算的输出指令。
- 随着房间温度的变化,Arduino也会调整空调设定温度。
int main(void) { init(); setup(); for(;;){ loop(); if (serialEventRun)serialEventRun(); } Return 0; } void setup(){ Serial.begin(9600); Initialize device. dht.begin(); Serial.println(F("DHTxx Unified Sensor Example)); //Print temperature sensor details. sensor_t sensor; dht.temperature().getSensor(&sensor); Serial.println(F("-------------------------")); Serial.println(F("Temperature Sensor")); Serial.print (F("Sensor Type:"));Serial.println(sensor.name); Serial.print (F("Driver Ver:"));Serial.println(sensor.version); Serial.print (F("Unique ID:"));Serial.println(sensor.sensor_id); Serial.print (F("Max Value:"));Serial.print(sensor.max_value); Serial.println(F("C")); Serial.print (F("Min Value:"));Serial.print(sensor.min_value); Serial.println(F("C")); Serial.print (F("Resolution:"));Serial.print(sensor.resolution); Serial.println(F("C")); Serial.printin((F("-------------------------")); //Print humidity sensor details. dht.humidity().getSensor(&sensor); Serial.println(F("Humidity Sensor")); Serial.print (F("Sensor Type: "));Serial.println(sensor.name); Serial.print (F("Driver Ver: "));Serial.println(sensor.version); Serial.print (F(Unique ID: "));Serial.println(sensor.sensor_id); Serial.print (F("Max Value: "));Serial.print(sensor.max_value); Serial.println(F("%")); Serial.print (F("Min Value: "));Serial.print(sensor.min_value); Serial.println(F("%")); Serial.print (F(Resolution:"));Serial.print(sensor.resolution); Serial.println(F("%")); Serial.println((F("-------------------------")); //Set delay between sensor readings based on sensor details. delayMS sensor.min_delay 1000; void loop(){ //Delay between measurements. delay(delayMS); //Get temperature event and print its value. sensors_event_t event; dht.temperature().getEvent(&event); if (isnan(event.temperature)){ Serial.println(F("Error readina temperature!")); } else{ Serial.print(F(Temperature:")) Serial.print(event.temperature); Serial.println(F("C")); } //Get humidity event and print its value. dht.humidity0.getEvent(&event); if (isnan(event.relative_humidity)){ Serial.println(F("Error reading humidity!")); } else{ Serial.print(F("Humidity:")); Serial.print(event.relative_humidity); Serial.println(F(%")); } }
7 PID控制详述
来源:5分钟,带你推导位置式PID和增量式PID公式~_哔哩哔哩_bilibili

增量式PID的优势
up主洋葱auto认为,之所以要分增量式PID是因为:
1.有的控制系统只需要输出控制增量,比如步进电机的控制。这种情况下用增量式正合适,没有积分计算,计算量也小。
2.对PID进行优化的时候,例如微分先行PID采用增量式PID表达式的时候,优化后的PID公式更简单,编程更容易,所以许多人喜欢用增量式表达式。
3.有的场景下需要做手动控制和自动控制的切换,用增量式表达式可以实现无扰切换。
增量式表达式由于每次输出都是基于上次的结果+增量部分的计算结果,因此切换的时候只有增量部分会重新计算,最后的输出扰动很小。
而位置式的要重新计算,PID控制的输出会比较大。
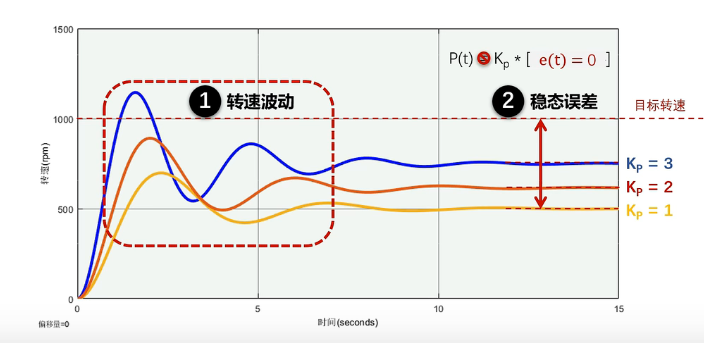
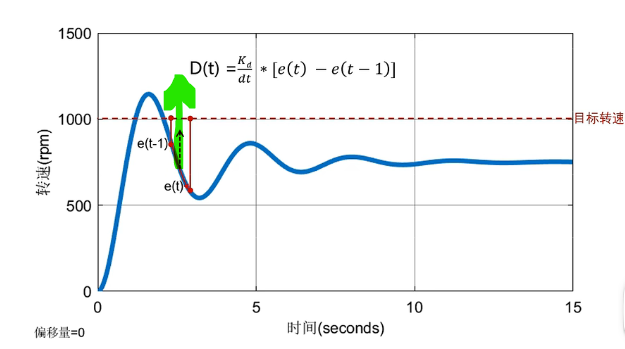
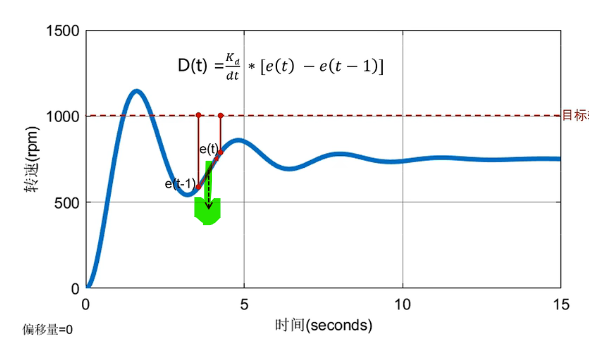
D像阻尼器,就像楞次定律hhh让目标更快达到稳态速度
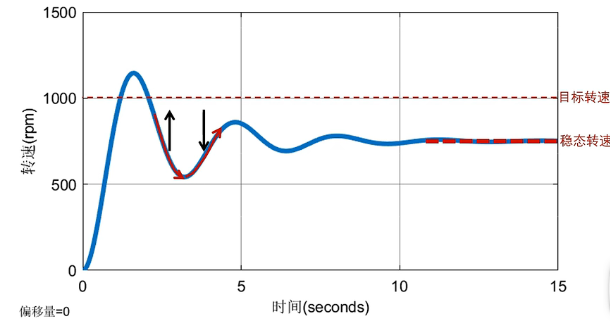
积分I则致力于消除第一个尖峰,即超调量
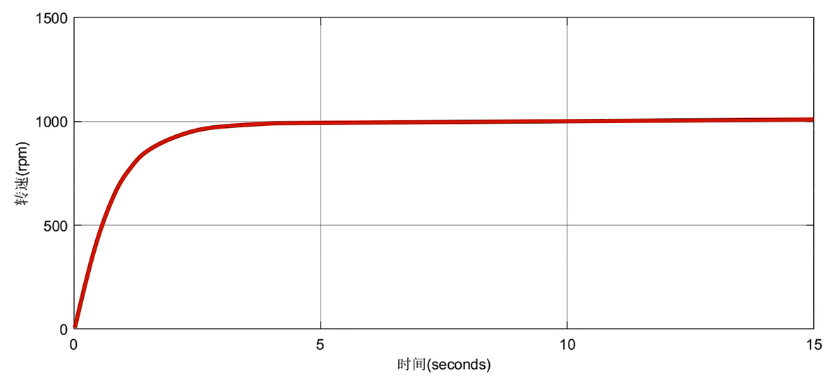
积分饱和
积分控制器的优化,应对积分饱和问题_哔哩哔哩_bilibili
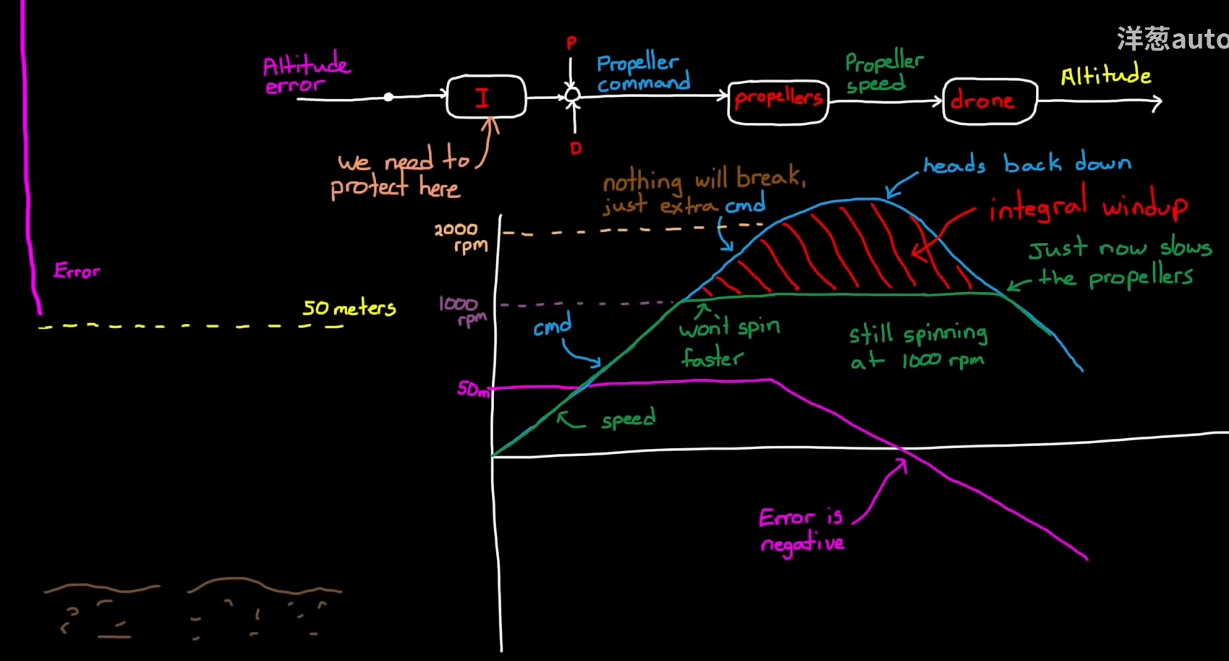
积分抗饱和!


保守一些→
微分饱和

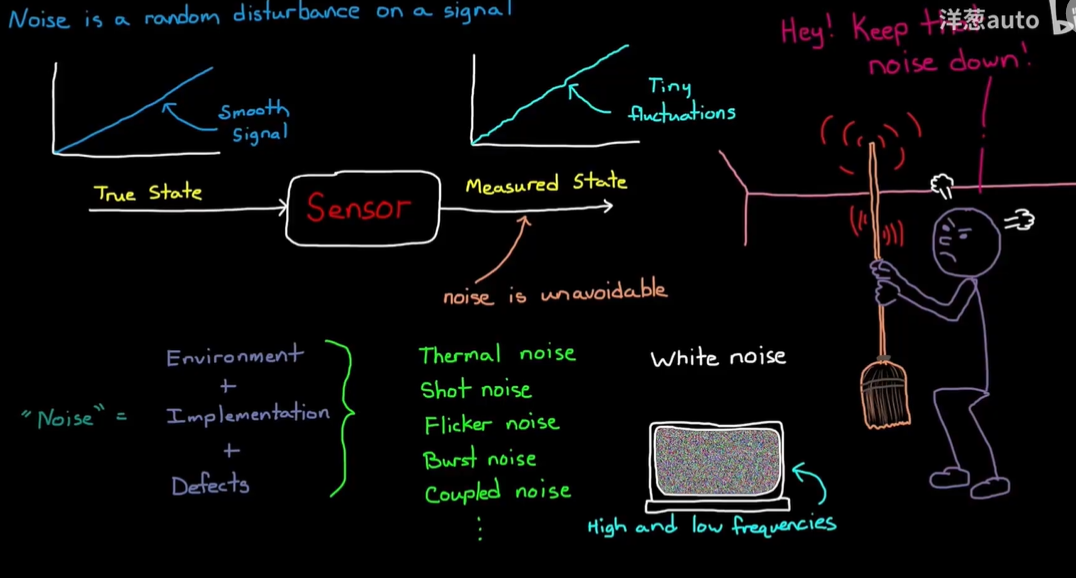
对某些控制方法,低振幅的噪声不会对控制系统产生太大的影响,噪声问题会被掩盖
但对理想的PID控制器,有纯微分控制通道,会放大高频信号,把小的、注意不到的扰动放大到可能影响系统的程度
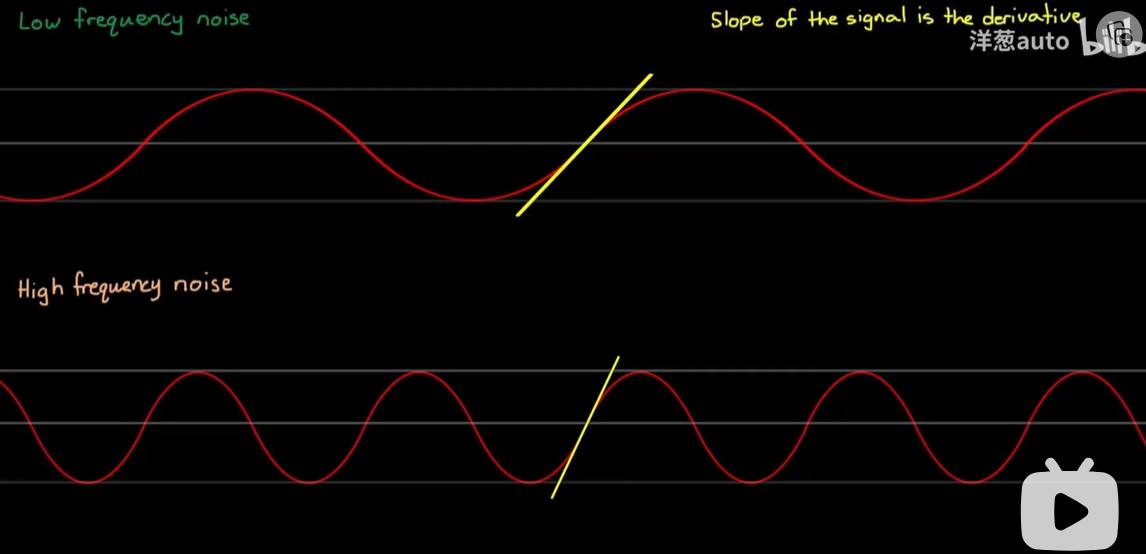
增大频率,虽然幅值没有改变,但斜率还是改变了。
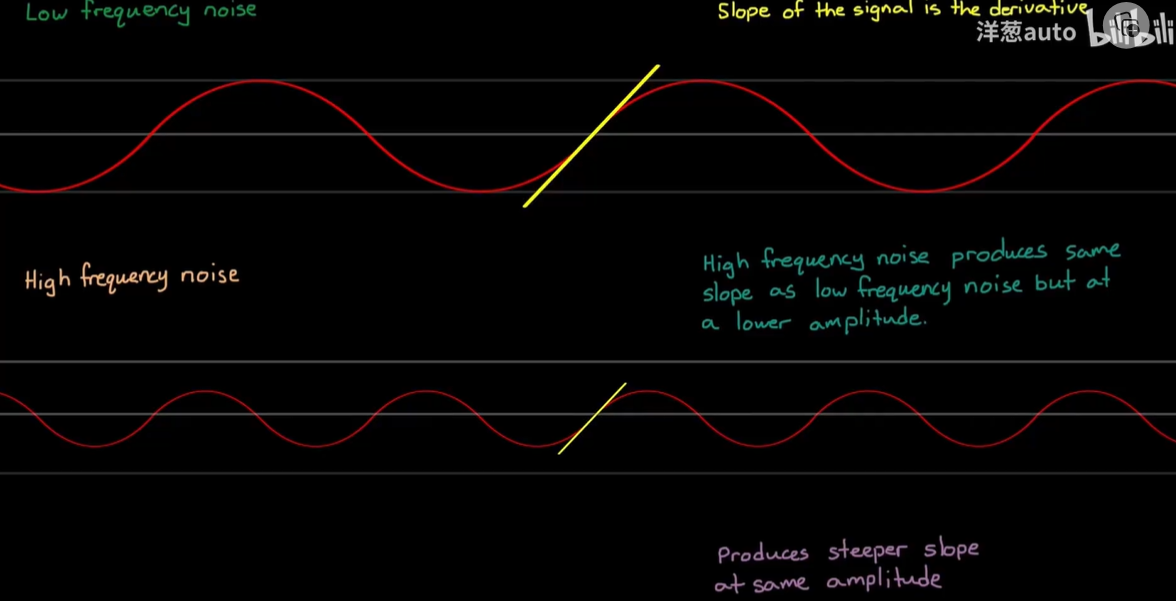
降低高频噪声的幅值,从而减小微分值。
而再增加频率,又会让斜率变大。
结论:如果系统存在高频噪声,即使其幅值可能很小,但经过微分器后也会对系统产生不小的影响 
8 PID调优指南
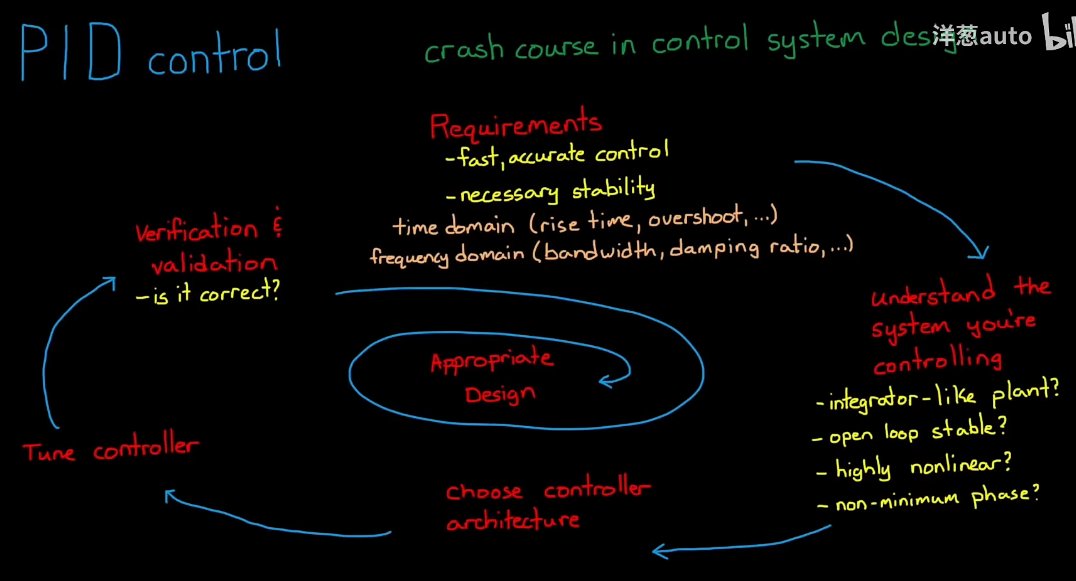
1、基于模型的调优
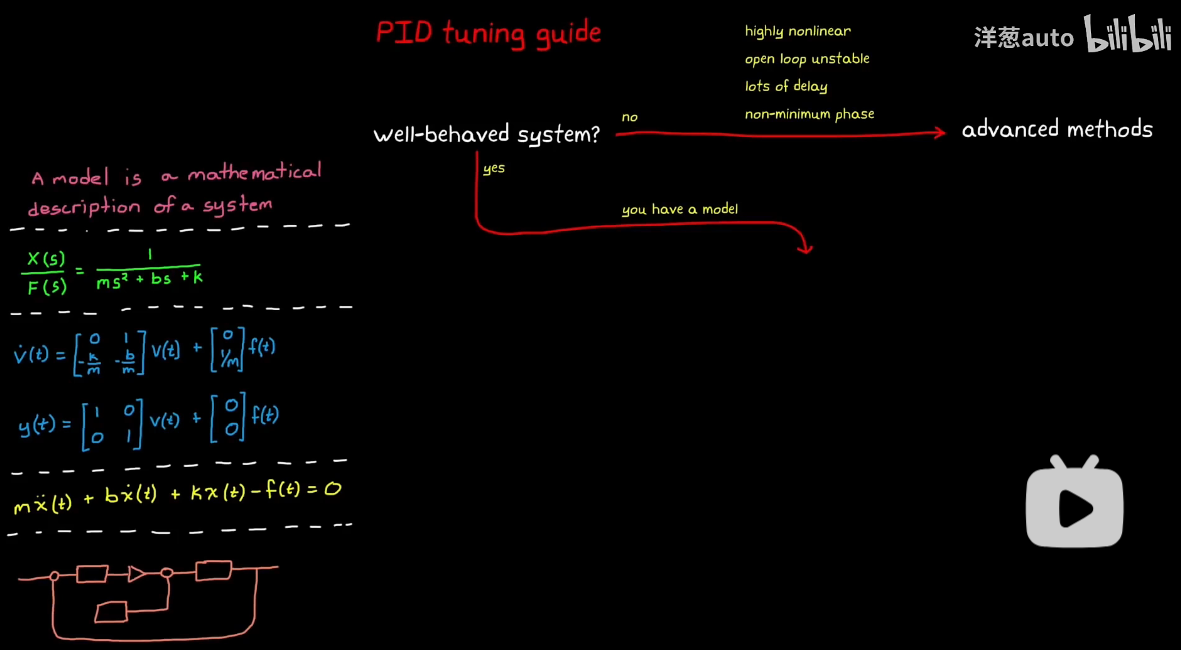

2.基于物理系统的设计
①手动调优
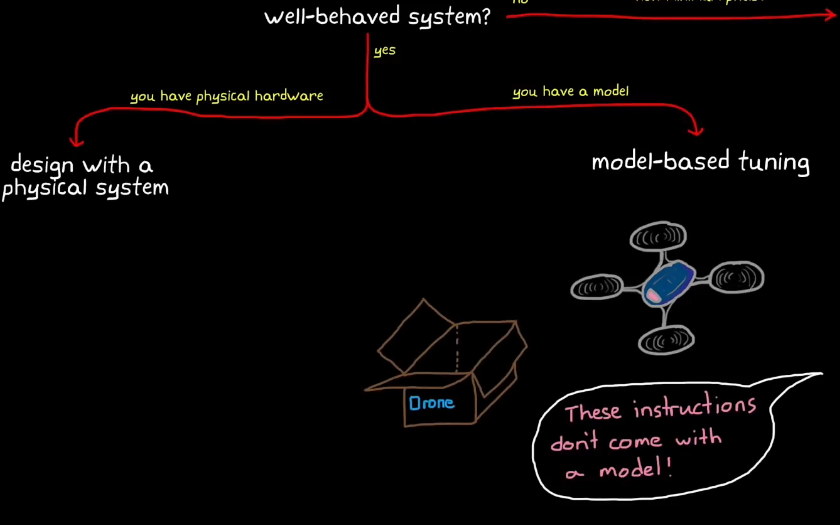

手动调节PID的增益系数,然后观察物理系统的实时响应,以逐渐将系统调整到理想状态
【注】
1、此调优过程的艺术性大于其技术性
2、需要了解每个通道对系统响应的影响
3、还要对PID增益如何影响系统有一定的感性认识,了解它们的特性后可以更好调优而不是瞎调
②在硬件上运行预定义的输入(常为阶跃输入),然后观察系统的开环响应
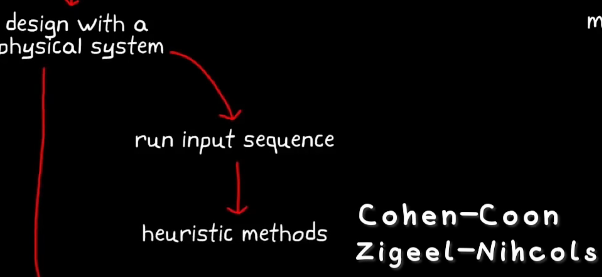
再采用一些启发式算法,不需要系统模型,只需要系统响应、振荡周期啥的就可以计算系统的初始增益
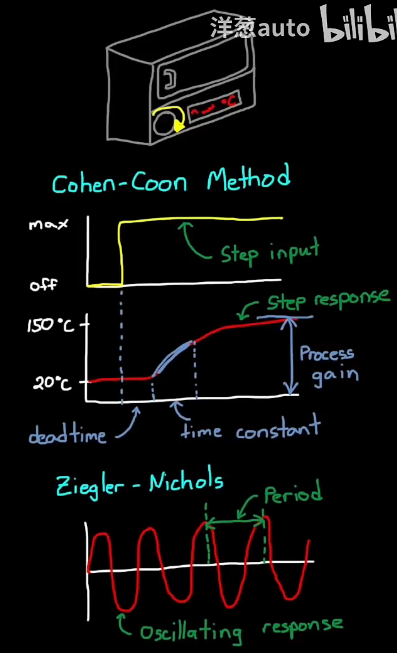
启发式算法只提供初始的猜测,运气好可能可以用,但之后往往还是需要手动调优以获得合适的参数
当然还可以对物理硬件进行建模


 浙公网安备 33010602011771号
浙公网安备 33010602011771号