信号与系统傅里叶级数、傅里叶变换及常用变换对和三角函数公式
傅里叶变换
傅里叶级数
周期信号的分析公式
$$\displaystyle{C_k=\frac{1}{T}\int_Tx(t)e^{-jk\omega_0t}dt} $$
周期信号的综合公式
$$x(t)=\sum_{k=-\infin}^{\infin}C_ke^{jk\omega_0t}$$
傅里叶变换对
$$f(t)\leftrightarrow F(\omega)$$
傅里叶(正)变换
$$F(w)=\int_{-\infin}^{\infin}f(t)e^{-jwt}dt$$
傅里叶反变换
$$f(t)=\frac{1}{2\pi}\int_{-\infin}^{\infin}F(w)e^{jwt}dw$$
三角函数公式
积化和差
$$sin\alpha cos\beta=\frac{1}{2}[sin(\alpha+\beta)+sin(\alpha-\beta)]$$
$$cos\alpha sin\beta=\frac{1}{2}[sin(\alpha+\beta)-sin(\alpha-\beta)]$$
$$cos\alpha cos\beta=\frac{1}{2}[cos(\alpha+\beta)+cos(\alpha-\beta)]$$
$$sin\alpha sin\beta=-\frac{1}{2}[cos(\alpha+\beta)-sin(\alpha-\beta)]$$
和差化积
(推导是上式角度和、差的一半)
$$sin\alpha+sin\beta=2sin\frac{\alpha+\beta}{2}cos\frac{\alpha-\beta}{2}$$
$$sin\alpha-sin\beta=2cos\frac{\alpha+\beta}{2}sin\frac{\alpha-\beta}{2}$$
$$cos\alpha+cos\beta=2cos\frac{\alpha+\beta}{2}cos\frac{\alpha-\beta}{2}$$
$$cos\alpha-cos\beta=-2sin\frac{\alpha+\beta}{2}sin\frac{\alpha-\beta}{2}$$
常用傅里叶变换对
$$e^{-a|t|} \leftrightarrow \frac{2a}{a^2+w^2}$$
$$e^{-at}u(t) \leftrightarrow \frac{1}{a+jw}$$
$$te^{-at}u(t) \leftrightarrow \frac{1}{(a+jw)^2}$$
$$\begin{cases} \displaystyle{1-\frac{|t|}{\tau}}& |t|<\tau\\ 0& |t|>\tau \end{cases} \leftrightarrow \tau(Sa\frac{\omega \tau}{2})^2$$
【反过来$÷2\pi$】
$$\begin{cases} \displaystyle{1-\frac{|\omega|}{W}}& |\omega|<W\\ 0& |\omega|>W \end{cases} \leftrightarrow \frac{W}{2\pi}(Sa\frac{Wt}{2})^2$$
$$|t| \leftrightarrow -\frac{2}{w^2}$$
$$\delta(t) \leftrightarrow 1$$
$$1 \leftrightarrow 2\pi\delta(\omega)$$
$$u(t) \leftrightarrow \pi\delta(\omega)+\frac{1}{j\omega}$$
$$cos\omega_0t \leftrightarrow \pi[\delta(\omega-\omega_0)+\delta(\omega+\omega_0)]$$
$$cos\omega_0t·u(t) \leftrightarrow \frac{\pi}{2}[\delta(\omega-\omega_0)+\delta(\omega+\omega_0)]+\frac{j\omega}{\omega_0^2-\omega^2}$$
$$sin\omega_0t \leftrightarrow j\pi[\delta(\omega+\omega_0)-\delta(\omega-\omega_0)]$$
$$sin\omega_0t·u(t) \leftrightarrow \frac{\pi}{2j}[\delta(\omega-\omega_0)-\delta(\omega+\omega_0)]+\frac{\omega_0}{\omega_0^2-\omega^2}$$
$$e^{-at}·sin\omega_0t·u(t) \leftrightarrow \frac{\omega_0}{(a+jw)^2+\omega_0^2}$$
$$e^{j\omega_0t} \leftrightarrow 2\pi\delta(\omega-\omega_0)$$
$$\frac{W}{2\pi}Sa\frac{Wt}{2} \leftrightarrow rect\frac{\omega}{W}$$
$$rect\frac{t}{\tau} \leftrightarrow \tau Sa\frac{\omega \tau}{2}$$
$$e^{-\frac{t^2}{2\sigma^2}} \leftrightarrow \sqrt{2\pi}\sigma e^{-\frac{\sigma^2\omega^2}{2}}$$
$$\delta_T(t) \leftrightarrow \omega_0\delta_{\omega_0}(\omega), \omega_0=\frac{2\pi}{T}$$
$$t·u(t) \leftrightarrow -\frac{1}{\omega^2}+j\pi\delta'(\omega)$$
常见函数的傅里叶变换及其图像
对比这些图像能产生对“时域与频域”更深刻的理解
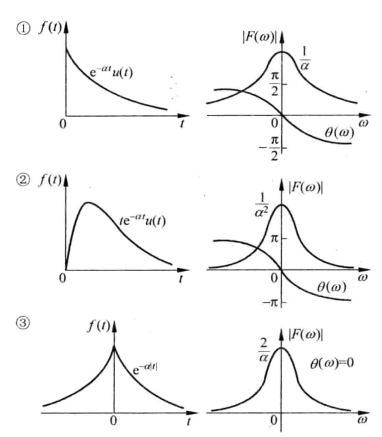
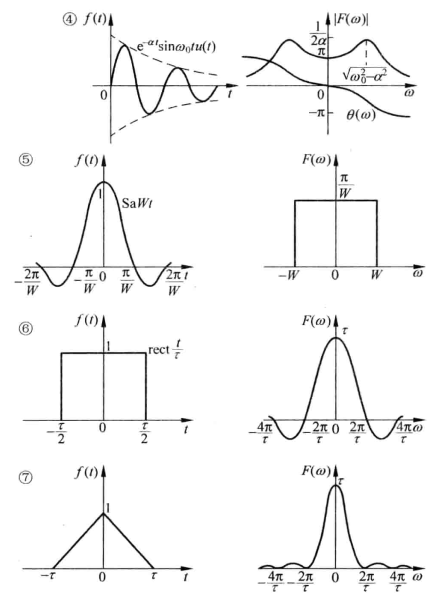
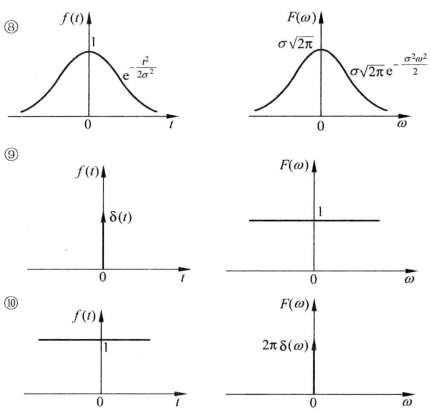
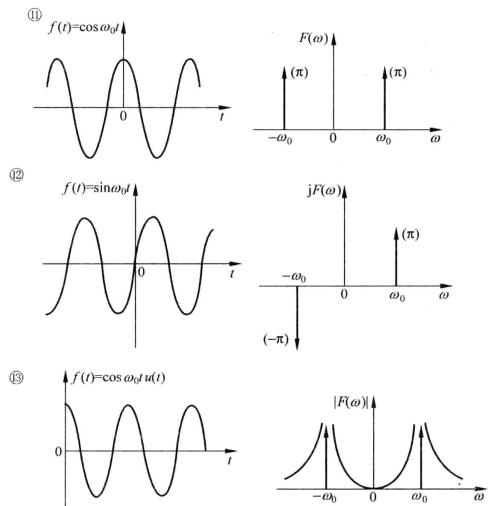
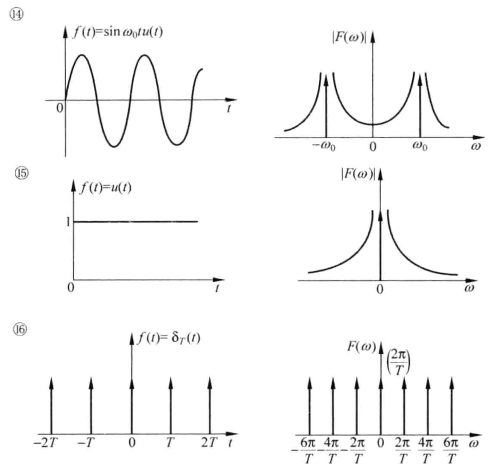
典型信号及其性质
1.正弦信号
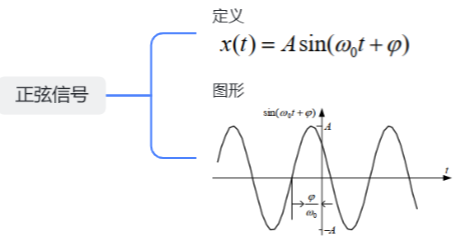
2.实指数信号
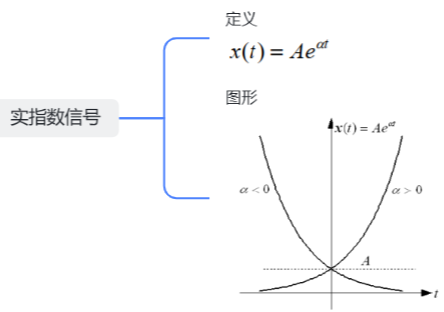
3.虚指数信号

4.复指数信号
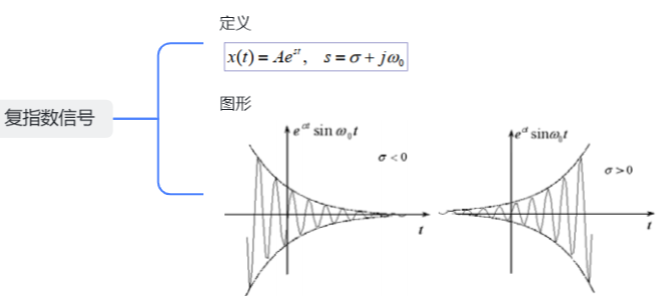
5.抽样信号
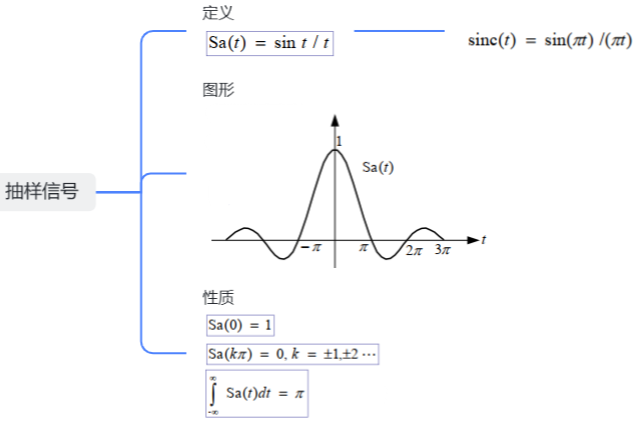
6.阶跃信号

7.斜坡信号
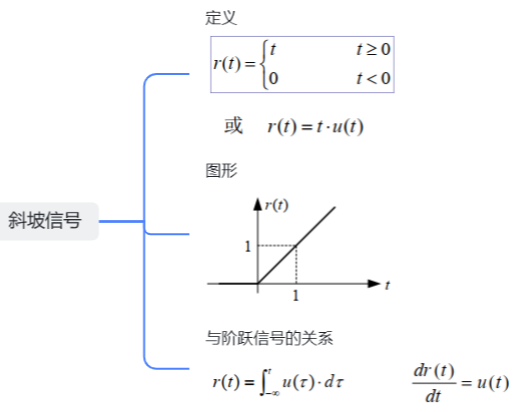
8.冲激信号
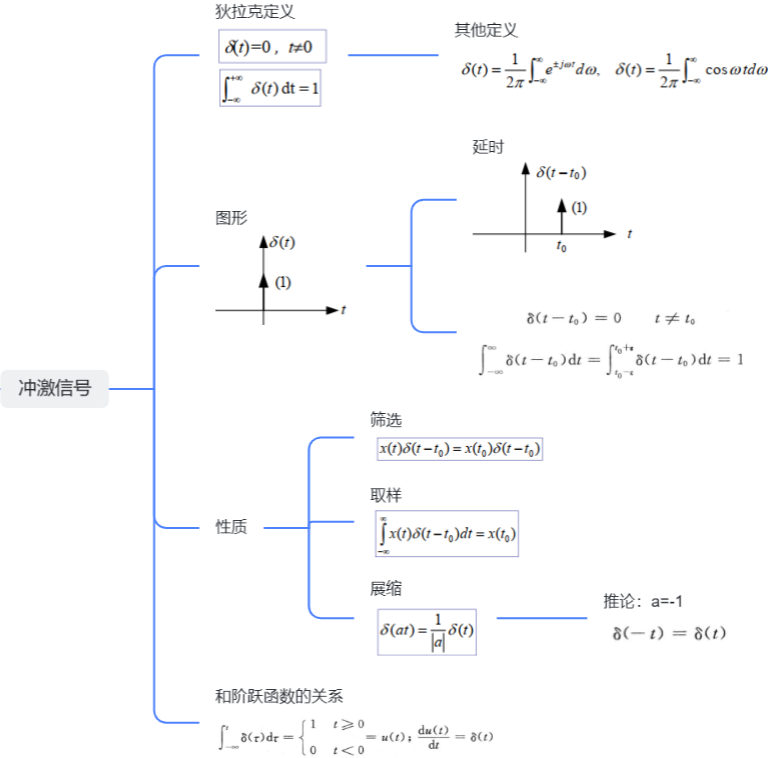
9.冲激偶信号
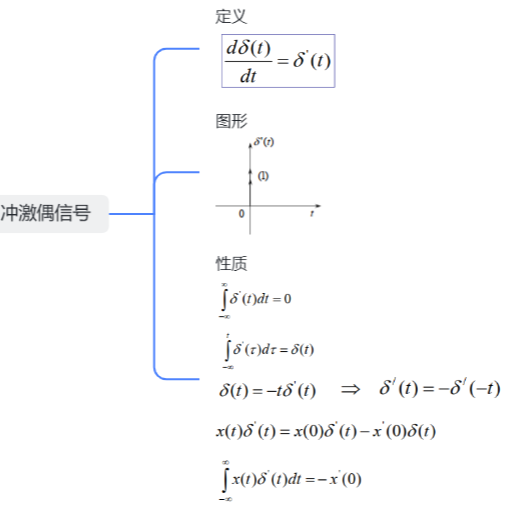
信号的典型运算
1.尺度变换
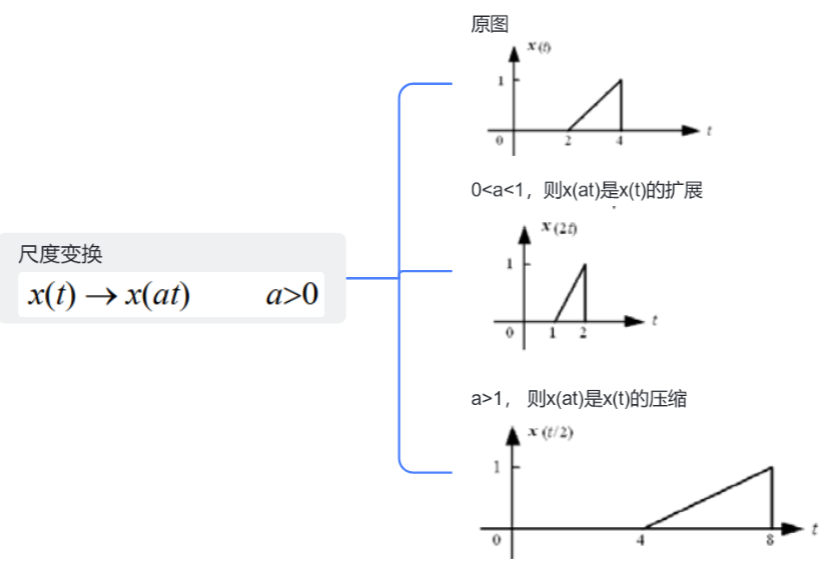
2.信号翻转
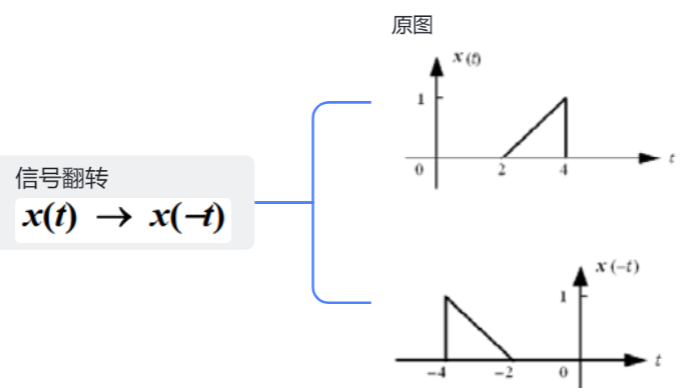
3.时移
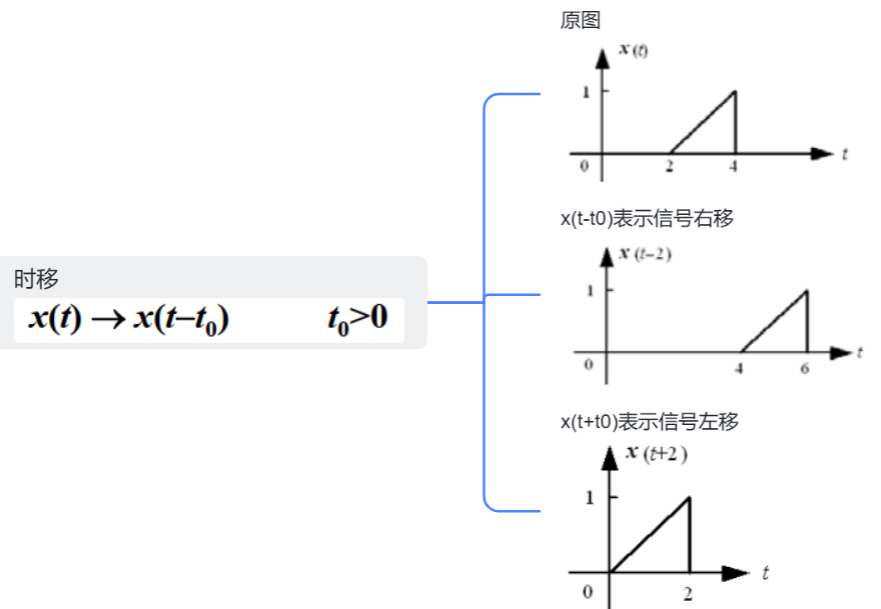
4.信号相加
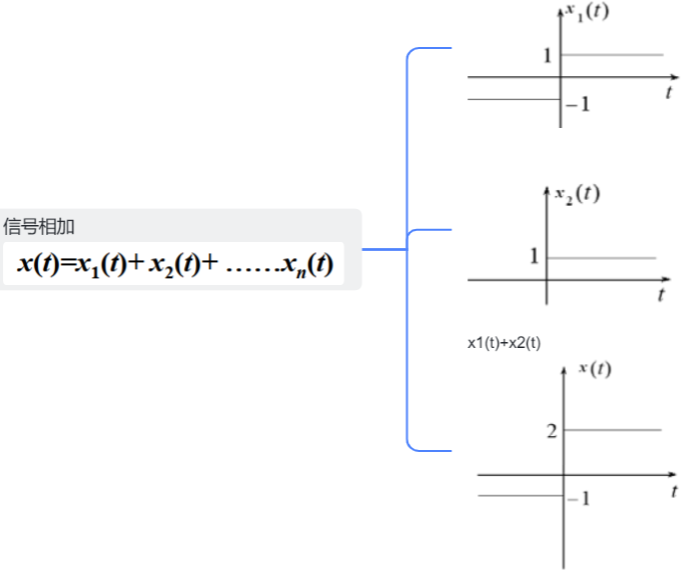
5.信号相乘
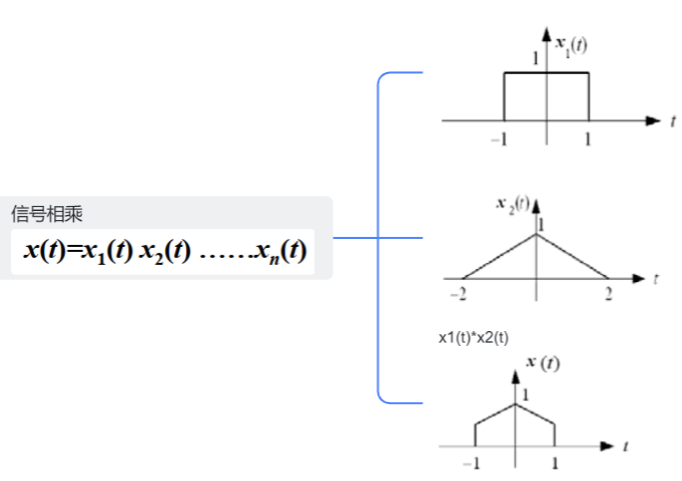
5.信号微分
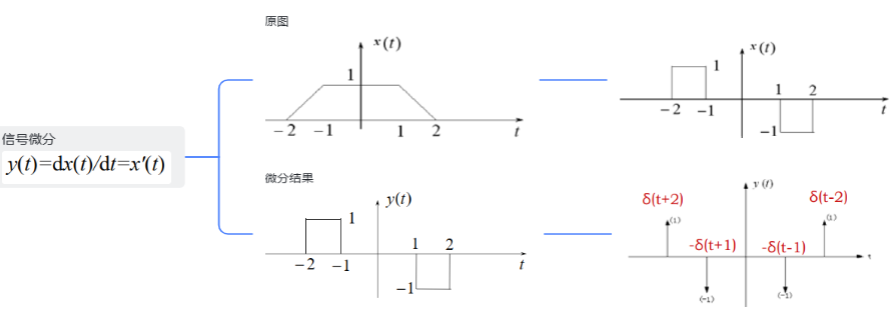
6.信号积分
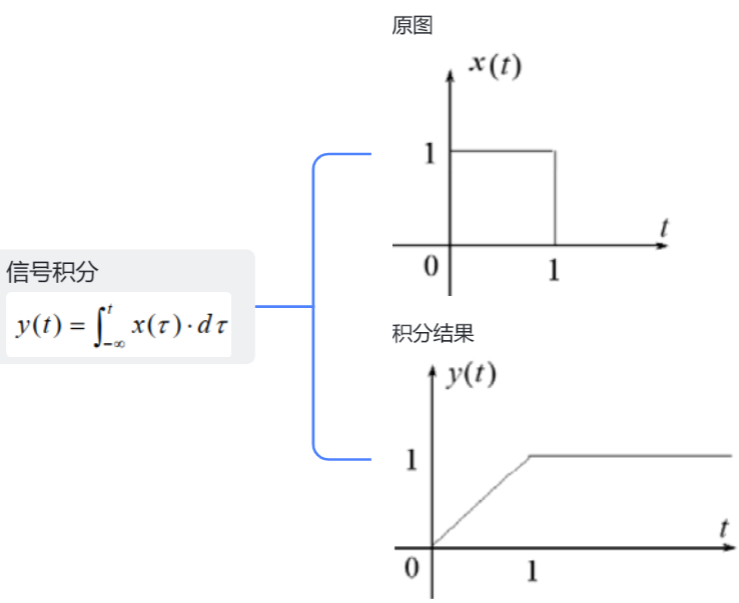
7.信号卷积
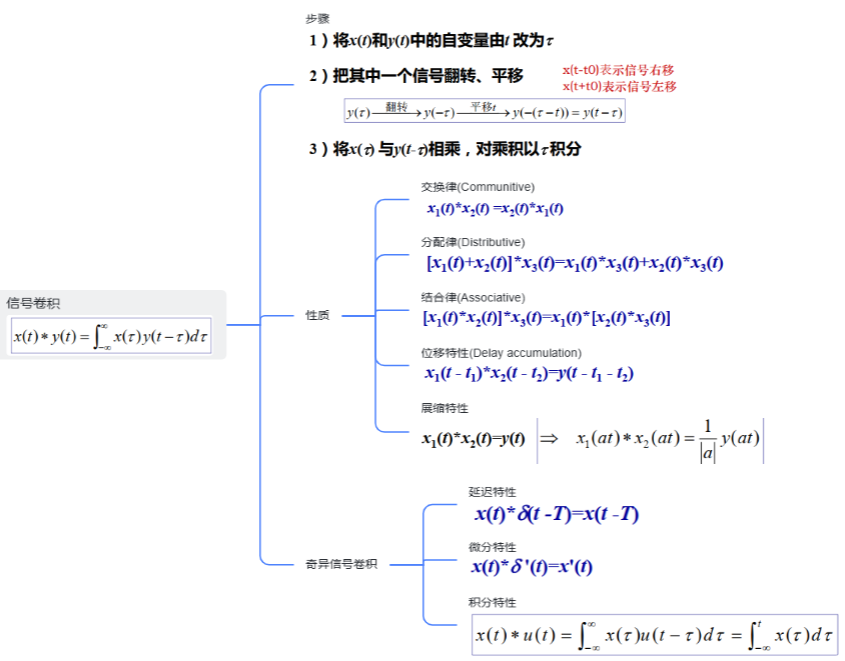
信号的分解
1.直流分量与交流分量
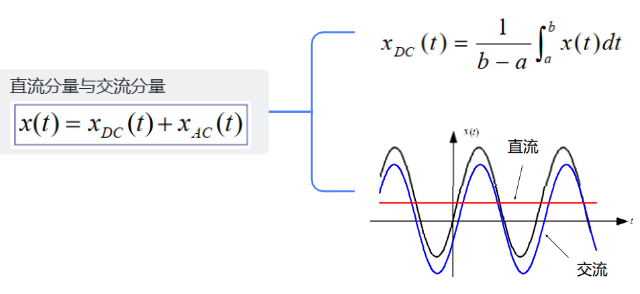
2.奇分量与偶分量
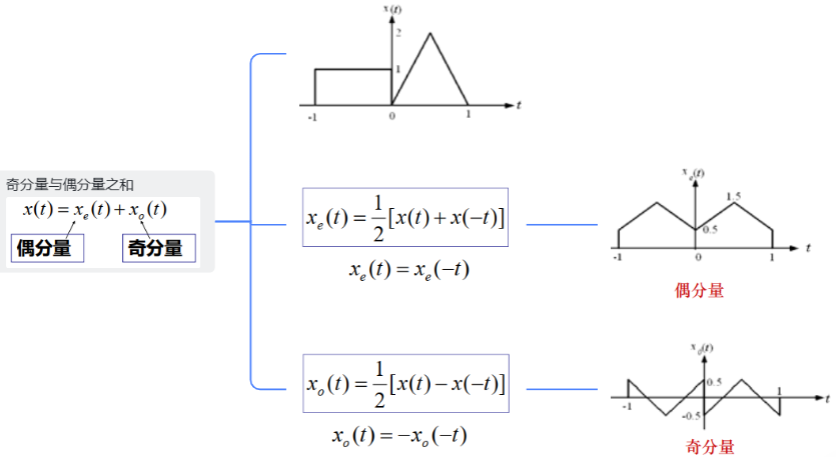
3.实部分量与虚部分量
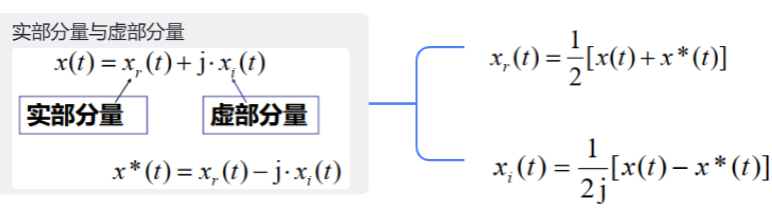
4.冲激函数的线性组合



