信道容量与香农信息论三定理、信道编码总结

1 信道容量定义

1.1 信道容量：信道中平均每个符号所能传递的最大互信息量$I(X;Y)$
$C=\mathop{max}\limits_{p(x)}{I(X;Y)}$，单位：bit /符号
1.2 单位时间t内信道容量：$\displaystyle{C_t=\frac{C}{t}}$，单位：bit/s
1.3 最佳输入概率$p(x)$分布时，传输的信息能达到信道容量
1.4 信道容量反映信道特性，表示信道传送信息的最大能力，是信道传输概率的函数，不同的转移概率对应不同的信道

2 信道编码定理

传送的信息量$R <$信道容量$C$，可以通过编码方法将全部信息几乎无差错传递到接收端，否则有信息损失

正定理：只要信息传输率R小于信道容量C， 总存在一种信道码（及解码器），可用所要求的任意小的差错概率实现可靠通信

逆定理：信道容量C是可靠通信系统信息传输率R的上边界。如果R > C，就不可能有任何一种编码能使差错概率任意小

3 香农信息论的三大定理

• 第一极限定理：无失真信源编码定理
• 第二极限定理：信道编码定理（离散、连续信道）
• 第三极限定理：限失真信源编码定理

3.1 离散信源的无失真信源编码定理

必存在一种编码方式，使得编码后的平均码长任意接近符号熵【方法：使概率与码长匹配】

3.2 离散或连续信源的限失真信源编码定理

离散无记忆信源X的信息率失真函数为$R(D)$
当信息率$R＞R(D)$，只要信源序列长度L足够长，一定存在一种编码方法，其译码失真小于或等于$D＋\varepsilon$，$\varepsilon$为任意小的正数；
反之，若$R＜R(D)$，则无论采用什么样的编码方法，其译码失真必大于$D$。

4 信道参数时变性影响信道容量性质

4.1 信道参数固定→信道容量固定
4.2 信道参数随时间变化→信道容量随信道参数变化而变化
此时用平均信道容量（遍历信道容量）衡量整体性能
中断信道容量：满足传输要求的信道容量下界

5 信道容量

5.1 离散单符号信道的信道容量

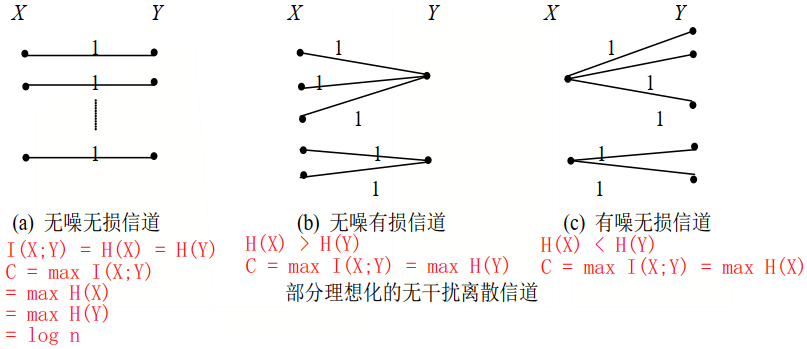
①对称DMC（离散无记忆信道）信道

 $\displaystyle{C=log_2m-H(Y|a_i)=log_2m+\sum^m_{j=1}p_{ij}logp_{ij}}$
$\displaystyle{H(Y)_{max}=log_2m, m}$输出符号类别数

 
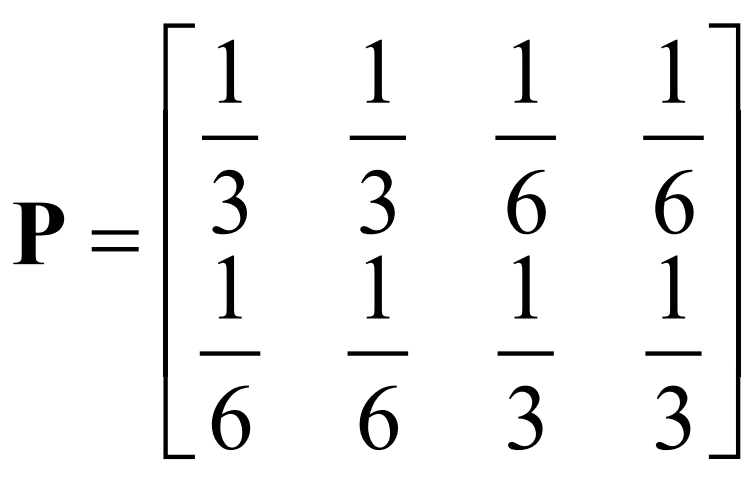
$C=log_24-H(\frac{1}{3},\frac{1}{3},\frac{1}{6},\frac{1}{6})$

强对称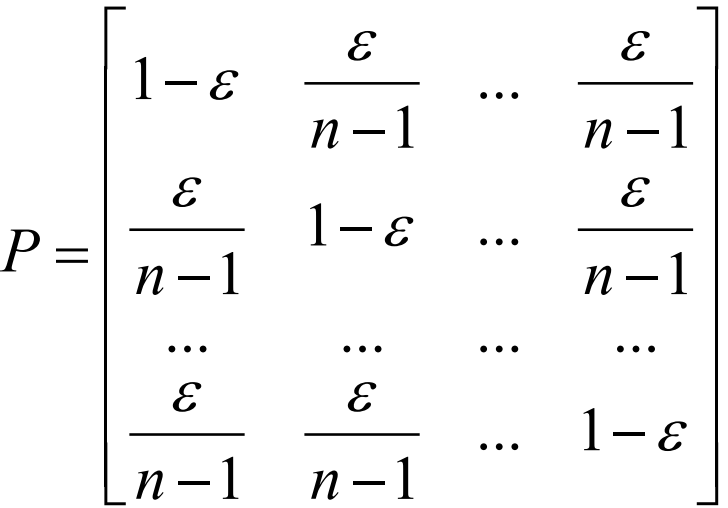
 $\displaystyle{C=log_2n-H(1-\varepsilon,\frac{\varepsilon}{n-1},\frac{\varepsilon}{n-1},\frac{\varepsilon}{n-1})}$

②串联信道

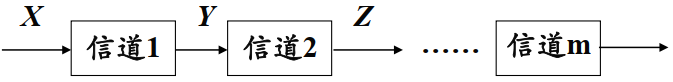
 信息不增$H(X)\geq I(X;Y)\geq I(X;Z)……$
$C(1)=max I(X;Y)\geq C(1,2)=max I(X;Z)……$

N个相同BSC（二进制对称）信道串联，转移概率矩阵$P=P_1^N$可特征分解

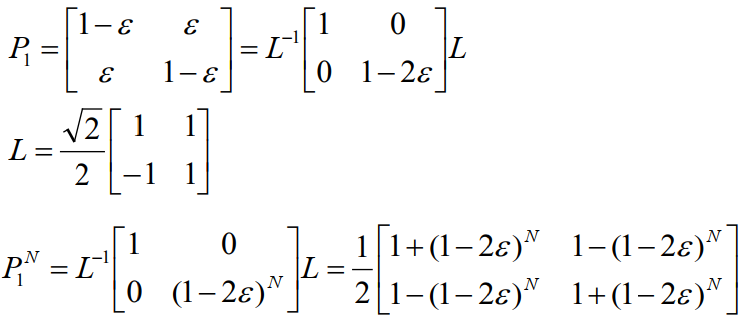
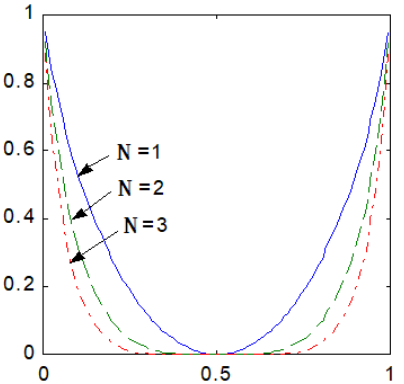
 $\displaystyle{C_N=log_22-H(\frac{1-(1-2\varepsilon)^N}{2})=1-H(\frac{1-(1-2\varepsilon)^N}{2})}$

$\displaystyle{\varepsilon \neq 0,1，N\to \infin, C_N→0}$

③准对称DMC信道 

 行（输入）对称，列（输出）不对称

【法一】$\displaystyle{C=\mathop{max}\limits_{p(a_i)}H(Y)-H(Y|a_i)，\frac{\partial C}{\partial p(a_i)}=0 \to p(a_i)}$

【法二】输入等概率分布时，达信道容量，故可直接算$\displaystyle{I(X;Y)=H(Y)-H(Y|X)=-\sum_jp(b_j)log_2p(b_j)+\sum_ip(a_i)\sum_jp(b_j|a_i)log_2p(b_j|a_i)}$

【法三】化为对称DMC信道子阵，按①方法计算
④一般DMC信道 

step1 求$\beta_j$：$\displaystyle{\sum_j p(y_i|x_i)logp(y_j|x_i)=\sum_jp(y_j|x_i)\beta_j}$

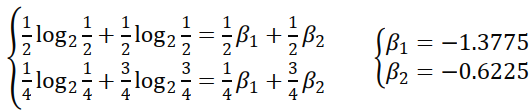
step2 求$C$：$\displaystyle{C=log(\sum_j 2^{\beta_j})}$

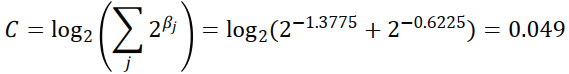
step3 求$p(y_j)$：$\displaystyle{p(y_j)=2^{\beta_j -C}}$

step4 求$p(x_i)$：解方程组$\displaystyle{p(y_j)=\sum_ip(x_i)p(y_j|x_i)}$

5.2 离散序列信道的信道容量

序列的转移概率之间有关联性，比无记忆的复杂得多， 至今没有有效求解方法（有时可用状态变量分析）

case1 信道无记忆 $\displaystyle{P(Y|X)=\prod_{l=1}^Lp(Y_l|X_l) \Longrightarrow I(X;Y)\leq \sum^L_{l=1}I(X_l;Y_l)}$

case2 信源无记忆$\displaystyle{P(X)=\prod_{l=1}^Lp(X_l) \Longrightarrow I(X;Y)\geq \sum^L_{l=1}I(X_l;Y_l)}$

case3 信源信道均无记忆 $\displaystyle{C_L=\sum^L_{l=1}C(l) \leq LC_1}$，信道平稳时取等号

①扩展信道

离散单符号信道→(L次扩展)→L次离散无记忆序列信道
2次扩展无记忆信道的信道容量正好是单符号信道的信道容量的2倍
离散无记忆N次扩展信道的信道容量$C^N=NC_1$

【联想知识点】离散平稳无记忆信源的N次扩展信源的熵$\displaystyle{H(X^N)=-\sum_{X^N}log_2P(X^N)=NH(X)}$

②独立并联信道 $p(y_1|x_1)p(y_2|x_2)p(y_3|x_3)…p(y_L|x_L)$，$C_{并}\leq \sum^L_{l=1}C_l$
③串联信道 $p(z|x)=p(y|x)p(z|xy)$
有马尔可夫性的串联信道 $p(z|x)=p(y|x)p(z|y)$

5.3 连续信道的信道容量

①连续单符号加性信道 

case1 噪声为加性高斯白噪声$\displaystyle{P_n(n)=N(0,\sigma^2)}$

噪声熵$\displaystyle{H_c(n)=\frac{1}{2}log2\pi e \sigma^2}$

信道容量$\displaystyle{C=\mathop{max}\limits_{p(x)}H_c(Y)-\frac{1}{2}log_2 2\pi e \sigma^2}$

【最大熵定理】输出平均功率为$P$，即$p_y(y)=N(0,P)$，当Y为正态分布时熵最大

$\displaystyle{P_n(n)=N(0,\sigma^2)}, x=y-n \Longrightarrow p_x(x)=N(0,S), S=P-\sigma^2$

信道容量$\displaystyle{C=\mathop{max}\limits_{p(x)}H_c(Y)-\frac{1}{2}log_2\frac{P}{\sigma^2}=\frac{1}{2}log_2(1+\frac{S}{\sigma^2})=\frac{1}{2}log_2(1+SNR)}$

case2 噪声为非高斯分布噪声（均值为$0$，方差为$\sigma^2$）

$\displaystyle{\frac{1}{2}log_2(1+\frac{S}{\sigma^2}) \leq C \leq \frac{1}{2}log_2 2\pi e P-H_c(n)}$

②多维无记忆加性连续信道

 等价于：L个独立并联高斯加性信道（条件：输入X中各分量统计独立，都是均值=0，方差为$P_l$的高斯变量）

$\displaystyle{C=\mathop{max}\limits_{p(x)}\sum^L_{l=1}\frac{1}{2}log_2(1+\frac{P_l}{\sigma_l^2})}$

case1 $\displaystyle{P_n(n)=N(0,\sigma^2)}$，$\displaystyle{C=\frac{L}{2}log_2(1+\frac{S}{\sigma^2})}$

case2 $\displaystyle{P_n(n)=N(0,\sigma_l^2)}$，输入信号总平均功率受限（$\displaystyle{E\big[\sum^L_{l=1} X_l^2\big]=\sum^L_{l=1} P_l=P}$）

合理分配各单元时刻信号平均功率，使信道容量最大

利用拉格朗日乘子法求解后得

各时刻信道输出功率相等：$\displaystyle{v=\frac{P+\sum^L_{l=1} \sigma_i^2}{L}}$

各时刻信号平均功率：$\displaystyle{P_l=v-\sigma^2_l=\frac{P+\sum^L_{l=1} \sigma_i^2}{L}-\sigma^2_l}$

信道容量$\displaystyle{C=\mathop{max}\limits_{p(x)}\sum^L_{l=1}\frac{1}{2}log_2(1+\frac{P_l}{\sigma_l^2})=\frac{1}{2}\sum^L_{l=1}log_2\frac{P+\sum^L_{l=1} \sigma_i^2}{L\sigma^2_l}}$

注水法：信噪比大的信道分得的功率多，信噪比小的信道分得的功率少，超过平均功率$v$则直接删除！

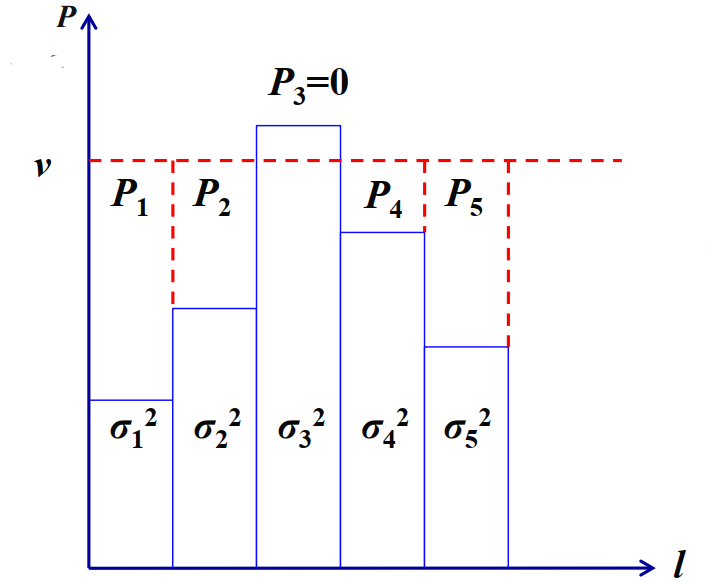
【无端联想】就像学校的总资源（如奖学金）是有限的，发奖学金不是会有个综合评价的标准化规则吗，在该套规则下得分高的自然会获得更多奖学金。

③波形信道

④限时限频限功率加性高斯白噪声(AWGN)信道

达到信道容量的输入信号：均值$=0$、平均功率$=P_s$（功率谱密度$\frac{N_0}{2}$）的高斯白噪声
香农公式$\displaystyle{C_t=\mathop{lim}\limits_{T→\infin}\frac{C}{T}=Wlog(1+\frac{P_s}{N_0W})=Wlog(1+SNR)}$