数电期末复习：由CMOS逻辑门电路列写逻辑表达式、 存储器与可编程逻辑器件、数模/模数转换、组合逻辑电路、触发器、时序电路、 状态分配、进制转换、逻辑代数、卡诺图
由CMOS逻辑门电路列写逻辑表达式
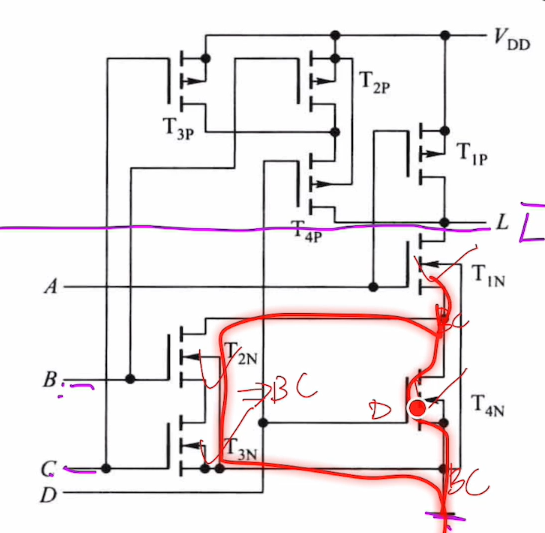
上下对偶，只看下面。
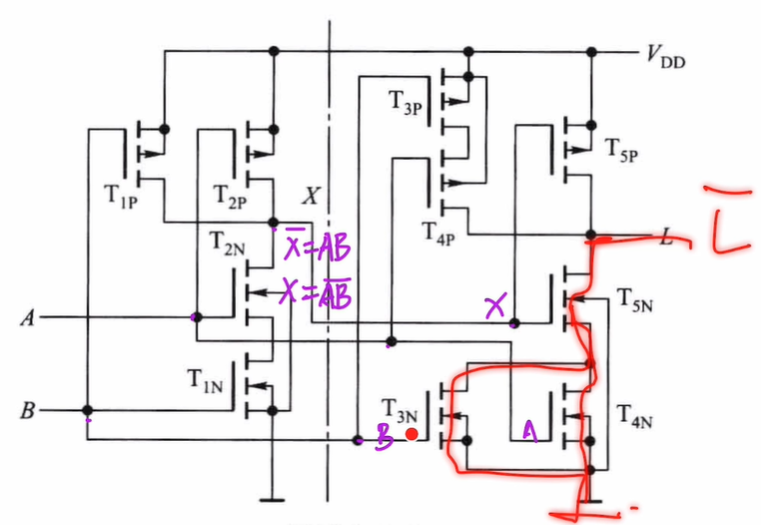
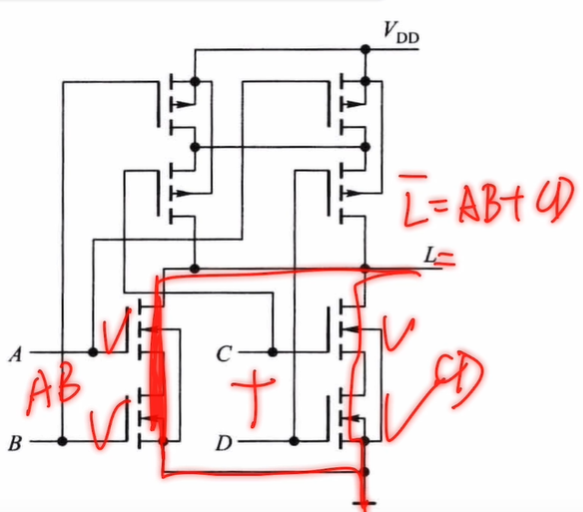
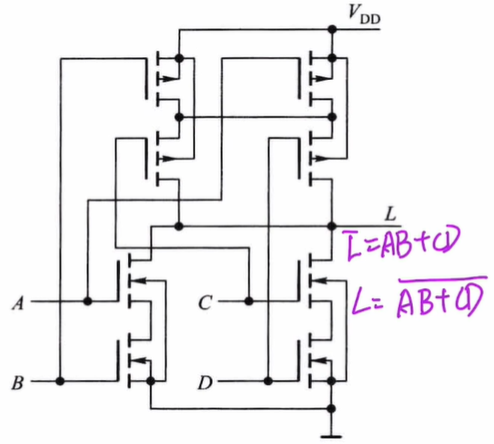
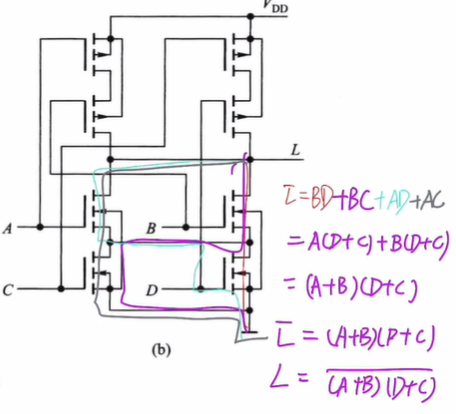【真的不难！模电-由CMOS逻辑门电路列写逻辑表达式】—— bilibili
（你想考OC一万次吗？？？）
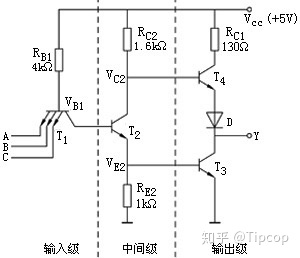
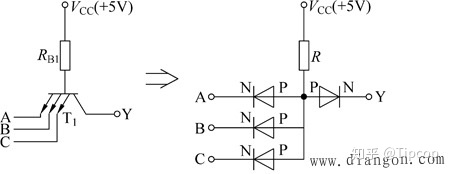
TTL与非门：下面的电阻分压拉高了输入的电平
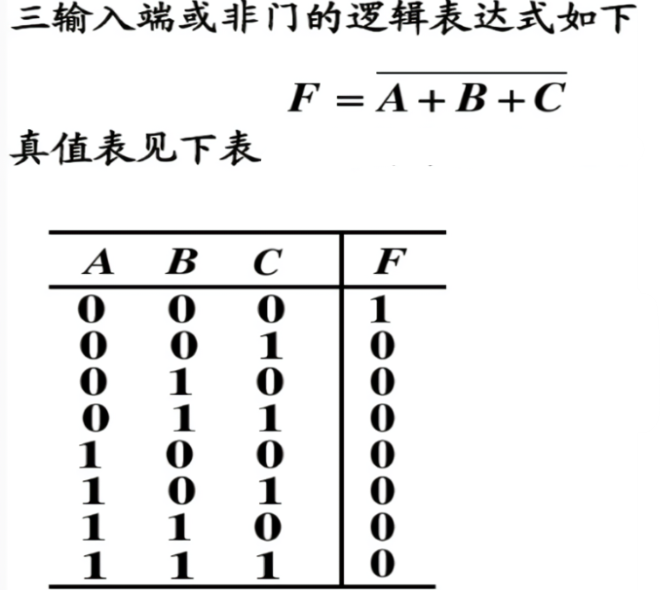
TTL电路多余的输入端的处理方式为：
（1）与门、与非门：多余的输入端输入高电平对逻辑功能无影响，可做以下方式处理：
①将多余的输入端串联限流电阻接高电平（电源VCC）；
②多余的输入端与有用的输入端并联使用，比如3输入端的与门电路只是用两个，可将第三个没有使用的输入端与1或2并联使用；
③多余的输入端直接悬空，由TTL电路可知，直接悬空也是相当于输入高电平的，因此可直接悬空；
④多余的输入端串联大于1kΩ的电阻接地，串联大于1kΩ的电阻接地也是相当于输入高电平，因此，从原理上来说也是可以。
但是为了提高电路可靠性，提高TTL电路的抗干扰能力，最好不要采用直接悬空或串联大于1kΩ的电阻接地的方法。
（2）或门、或非门：多余的输入端输入低电平对逻辑功能无影响，可做以下方式处理：
①接低电平（地）；②串联小于1kΩ电阻接地。
注意：串联电阻应远小于1kΩ以提高抗干扰能力。最好方法直接接地即可。这时多余的输入端是不允许悬空的，悬空相当于高电平就会影响逻辑功能。
CMOS反相器
拓展：CMOS逻辑电路多余的输入端是绝对不允许悬空处理的！
CMOS逻辑电路，内部是由MOS管电路组成的，MOS管是压控元件，其控制端电流很小，输入阻抗极高，多余的输入端悬空很容易受到外界的干扰。
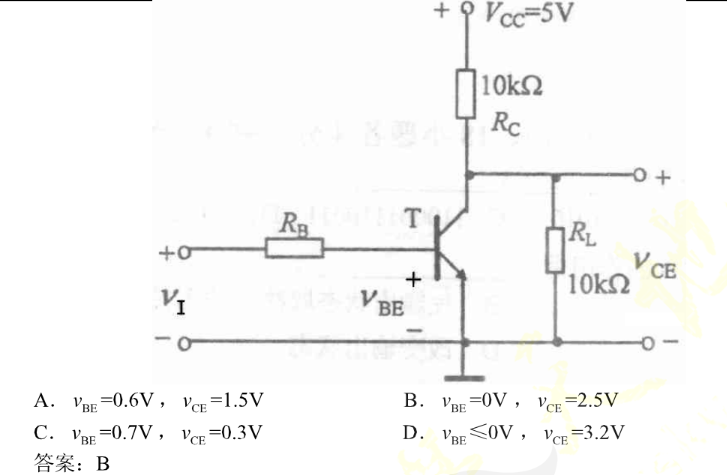
存储器与可编程逻辑器件
$2^{10}×8=1024×8=8192=8K或2^{10}×$
数模/模数转换
Digital（数字） analog（模拟），故应该是数模转换
（1）的$V_X=3.5V, V_N>V_X$就增加精度！
$0.02*{(11011010)}_2→{(218)}_{10}$
答案：BC
【数字电路=组合逻辑电路+时序逻辑电路】
组合逻辑电路：任何时刻输出信号，与该时刻的输入信号有关，与电路原来所处的状态无关（全加器、译码器、编码器、数据选择器）
时序逻辑电路：任何时刻输出信号，与该时刻的输入信号有关，与电路原来所处的状态有关（寄存器、移位寄存器）
组合逻辑电路
全加器
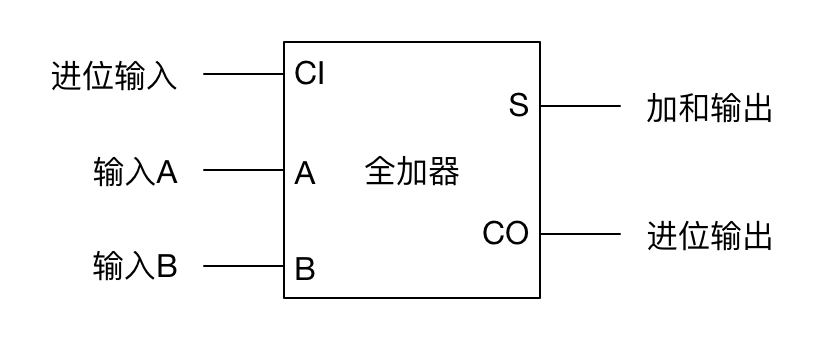
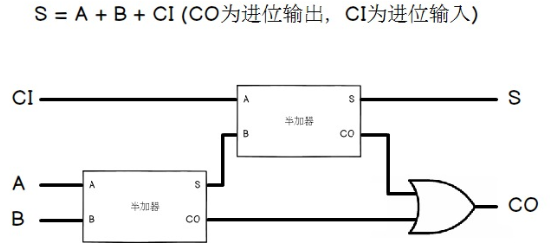
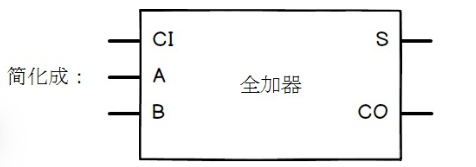
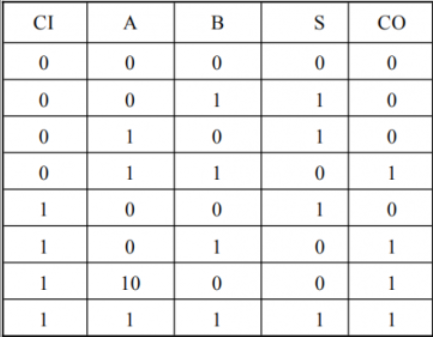
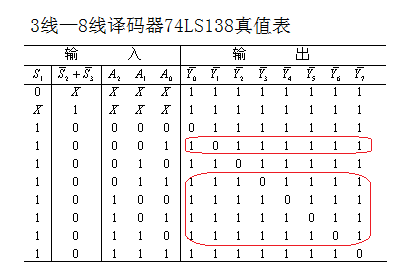
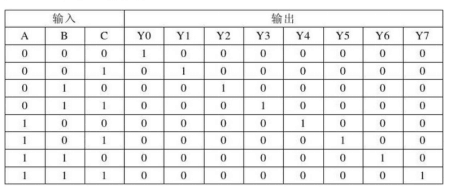
左右真值表的区别在Y有无取反
八路数据分配器的地址输入(选择控制)端有8个。 （错误）
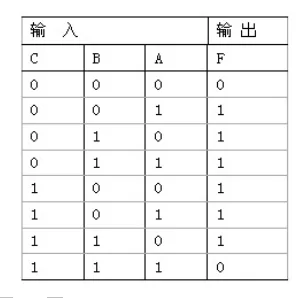
一个8选1的数据选择器有3个地址输入端，8个数据输入端。2的n次方路数据需要 n个地址输入端。
触发器
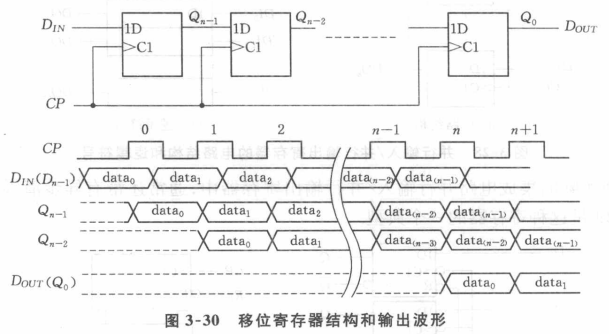
每个时钟脉冲只接收1位数据，数据同时在寄存器的各个触发器间移动，方向取决于内部输入输出连接方式
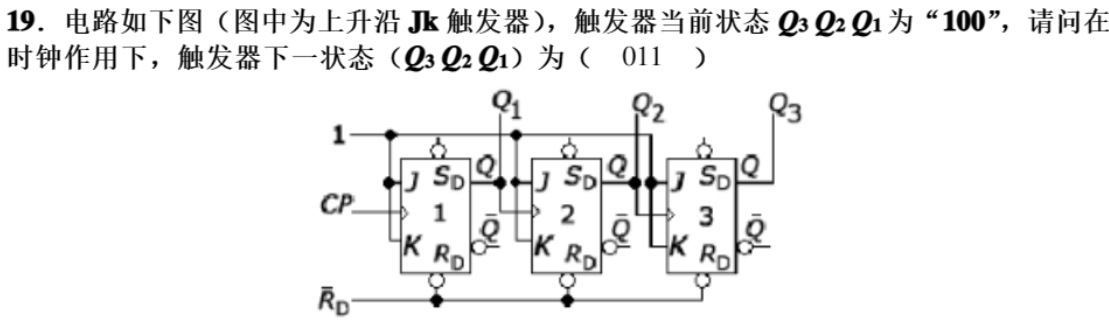
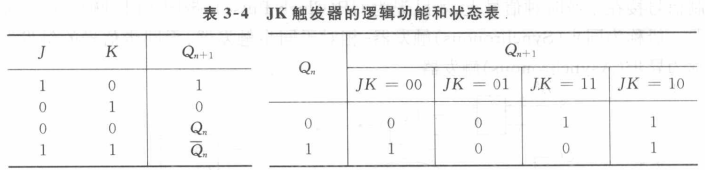
三个触发器JK端都接１，会翻转
时序电路、 状态分配
应该是电路不存在无效循环！
计数器自启动条件：一旦进入冗余态，可以在有限个时钟脉冲内脱离冗余状态，进入正常计数循环（eg2）
进制转换
hex：一种逢16进1的进位制。通常用数字0、1、2、3、4、5、6、7、8、9和字母A、B、C、D、E、F（a、b、c、d、e、f）表示
OCT：一种以8为基数的计数法，采用0，1，2，3，4，5，6，7八个数字，逢八进1。
格雷码和二进制码互相转换
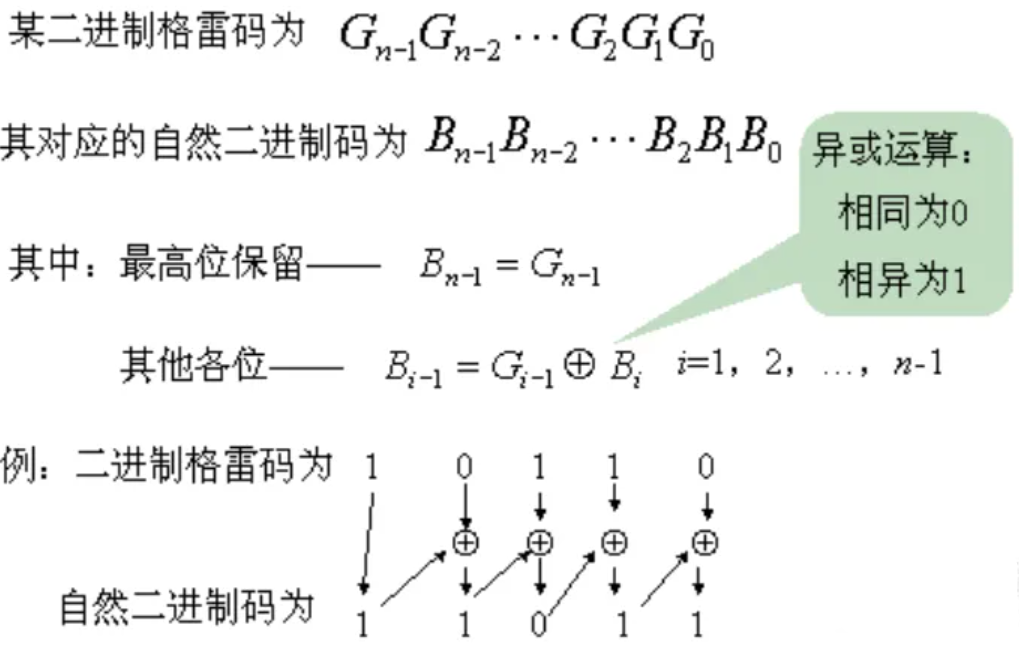
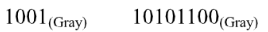
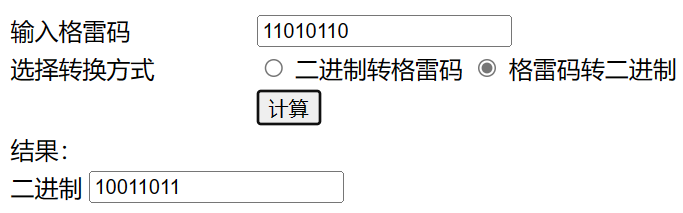
逻辑代数
（t2冗余律比较难： $A\overline{B}+CB=A\overline{B}+CB+AC$，别忘了t4的对偶律）
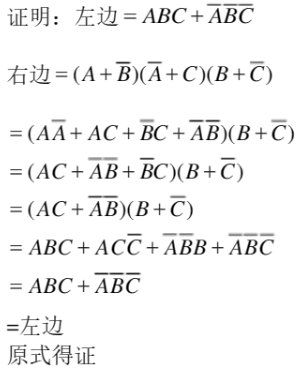
卡诺图
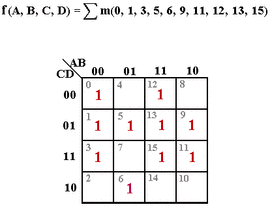
逻辑函数的约束条件在卡诺图中可0可1，为什么？
你的问题在于混淆了卡诺图与逻辑函数运算结果，要把脑袋中的卡诺图与逻辑函数运算结果这两个概念解耦。
首先明确约束项运算结果必定为0，故在逻辑函数中写不写均可。
然后将卡诺图理解为逻辑函数（注意与逻辑函数运算结果无关），卡诺图写1表示逻辑函数中“此项必不可少”，写0表示逻辑函数中“此项禁止出现”，X表示“此项出现与否无关”。
最后，X为1时，逻辑函数中出现该项，但该项运算结果始终为0；X为0时，逻辑函数中未出现该项。
逻辑变量之间的约束关系称为约束，即把不允许出现的对应组合对应的最小项称为约束项，约束项在不同的情况下用不同的字母来表示。
约束项需要人为强行“不让它出现或加以限制”，在这个条件下，用卡诺图化简逻辑函数时，可以在卡诺图对应的方格中写人“1”或“0”。
从这里也可以看出，含有约束项的逻辑函数在用卡诺图进行化简时，约束项对应的方格中的“1”只是-一个“表象”，它实际上是不存在的，即实际上是“0”。
正因为如此，才将它称为无关项，即有时将约束项认为是1，有时又可将其认为是0，完全视需要而定，取1或取0都不会影响其函数值，不会影响电路设计的结果。但是，如果客观上约束项出现了，它的取值不等于0了，则电路的输出就会出现错误。
任意项则不然，任意项无需人为对这些变量取值进行干预,这些变量取值就可以出现，对应的函数值是1还是0皆可，并不影响电路的逻辑功能。还可以看出，约束项通过电路的设计是可以转化为任意项的。使输人变量的取值在变化的过程中不受限制，提高了电路的可靠性。
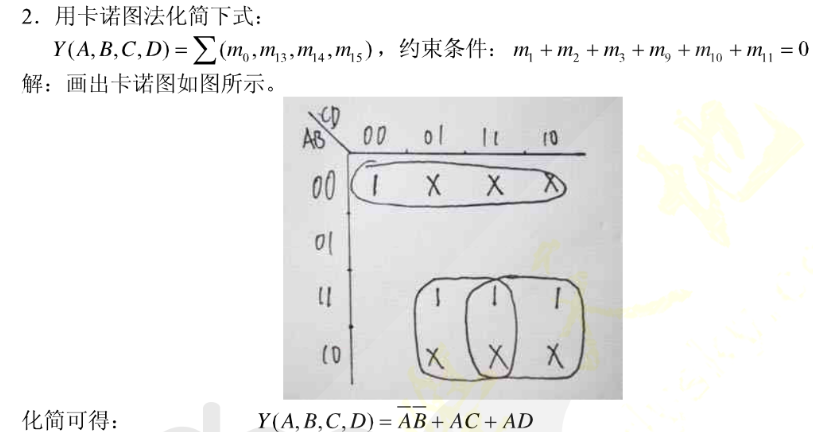
参考文献：
