同步时序电路设计(一般设计过程、自启动eg2、有冗余状态的设计、算法状态机方法、状态分配问题)
1 一般设计过程
根据给定时序逻辑问题的功能要求,经适当步骤,得到解决问题的电路
①分析功能要求、时序图,设计描述电路的有限状态机
状态机:用状态转换表或状态转换图描述了时序电路所有信息的时序电路
有限状态机FSM:描述时序电路的通用模型,在有限状态内完成一个时序电路问题的所有操作
有限:该状态机中状态数有限,包含的信息量有限
设计状态机的步骤
(1)确定米利还是摩尔模型
(2)由问题描述初步得到状态转换表/状态转换图
(3)分析得到的状态转换表/状态转换图,化简冗余状态,得到简单的状态机
②用实际逻辑电路(触发器、其他组合逻辑电路)实现有限状态机
得到逻辑电路的步骤
(1)给每个状态赋予适当二进制码
(2)确定采用的触发器类型,并根据状态编码、触发器类型、有限状态机状态转换关系得到电路状态激励表
(3)由激励表得触发器激励方程,由转换表得电路输出方程,按要求化简
(4)由表达式得到最终电路
eg.1摩尔模型

①确定采取何种时序电路模型
![]()
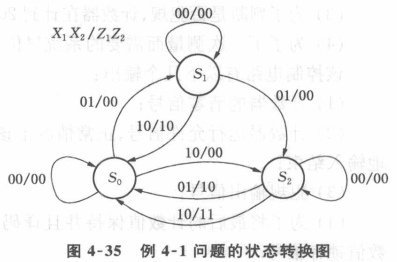
②构造状态转换表/图

为了方便设计与修改检验,建立状态时应该写好对状态的文字描述
本题输入常为1,即复位状态
$S_0$:复位状态。
a.下一个时钟脉冲检测到$X=0$,输入有效,系统进入下一个状态$S_1$
b.$X=1$,输入无效,系统回到状态$S_0$
$S_1$:检测到1个"0",输出0。
a.下一个时钟脉冲检测到$X=0$,输入有效,系统进入下一个状态$S_2$
b.$X=1$,输入无效,系统回到状态$S_0$
$S_2$:检测到2个或2个以上"0",输出0。
a.$X=0$,第一种情况:电路回到本状态等待下次输入“1”后产生输出
输入 1111 0001 1101 1001 1111
输出 0000 0001 0000 0001 0000
(第二种情况:只有"001"才有输出1,本题不是这样考虑的
输入 1111 0001 1101 1001 1111
输出 0000 0000 0000 0001 0000)
b.$X=1$,完成事件检测,系统进入下一状态$S_3$
$S_3$:检测到一个有效事件“001”输入,输出1。
a.下一个时钟脉冲检测到$X=0$,输入有效,可能输入新事件,进入$S_1$
b.$X=1$,等待事件输入,回到状态$S_1$
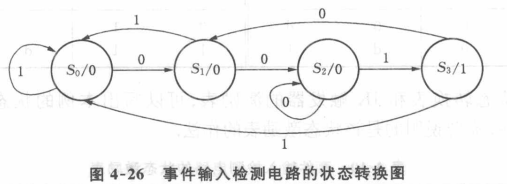
(状态转换图/表的)互补原则:从任意一个状态到两个不同状态的转换条件不可同时为逻辑1,即输入条件有互补关系
③状态化简与编码
本题已最简:$S_0=00,S_1=01,S_2=11,S_3=10$
④建立触发器状态激励表
(一般同步时序电路:JK触发器,计数器类:T触发器,寄存器类:D触发器)
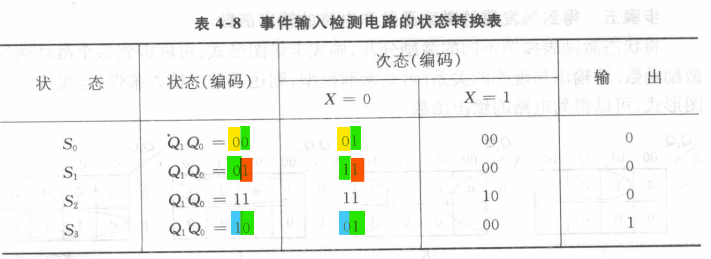
上面的图,根据下表现态到次态需要的JK激励条件得到状态激励表


⑤得到触发器激励函数,电路输出函数
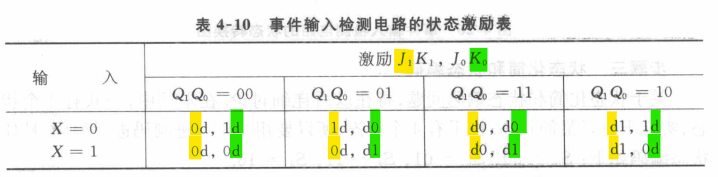

$J_1=\overline{X}Q_0,K_1=\overline{Q_0},J_0=\overline{X},K_0=X$
输出$Z$也是画卡诺图,得$Z=Q_1·\overline{Q_0}$
⑥根据第五步,画出逻辑图
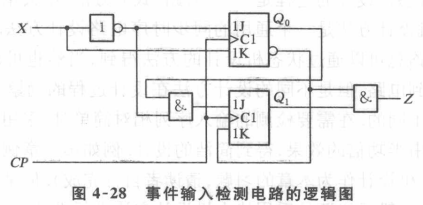
本例有效输入序列在最后3个时钟的检测结果是“001”,与下面的图功能一致
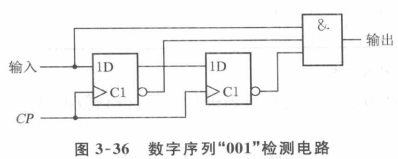
来自 文章(点我)
定位: 2 寄存器 ④用寄存器构成延时单元 eg2:“001”数字序列检测电路
【对比两电路异同】
(1)设计过程:就数据序列检测而言,D触发器视为延时器件比状态机设计法直观
(2)数据流:数据流一定和时钟同步用图3-36;本例输入不一定和时钟同步
要用3-36对本例数据流检测,需要在移位寄存器前再串个D触发器起同步作用(米利模型改成摩尔模型)
(3)要检测的序列比较长:状态机设计得到结果的复杂度更小,更经济
eg.“至少连续6个0,及随后1个1有效”:寄存器延时法,米利模型需6个,摩尔模型需7个;状态机设计法,8个状态只需3个触发器。
“至少4个连续0,及随后4个1有效”:寄存器延时法,米利模型需7个,摩尔模型需8个;状态机设计法,9个状态只需4个触发器。
(4)要检测的序列比较复杂:用寄存器延时概念做比较困难
总结:1.需要检测的输入序列相对简单→寄存器延时法
1.需要检测的输入序列相对复杂→状态机设计法
eg2.米利模型 自动售饮料机
自动售货机:可投1元或5角,饮料1.5元一杯,多了要找零(投2元找5角)
需要完成的功能:①记忆已投入的硬币数量
②根据硬币的数量确定是否送饮料和找零

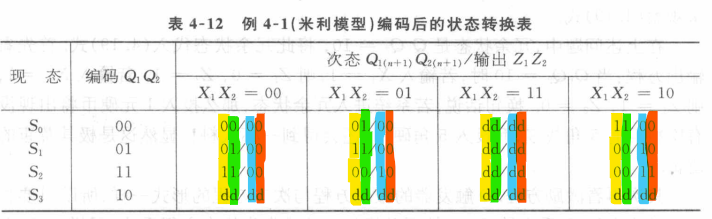
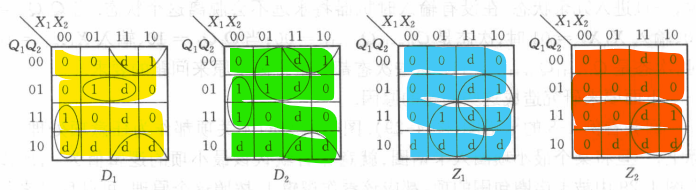
激励函数D,输出函数Z
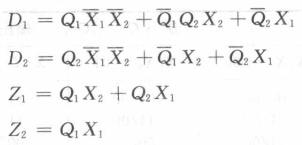
还有最后逻辑图,不画啦
2 有冗余状态的设计(假设系统可能进入冗余状态)
实际的状态数大于要求的状态数(上例把冗余当作任意项,不一定合理)
eg1.

根据上面卡诺圈圈起来的情况,可以得到
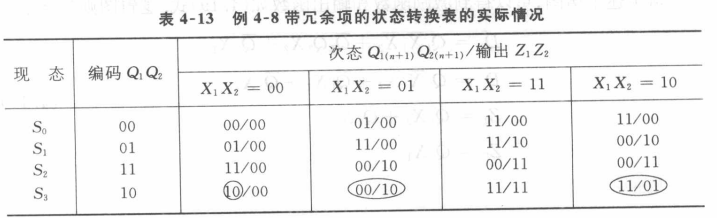
不合理之处:eg.状态10,输入$X_1X_2=00$时次态是10; 输入$X_1X_2=11$不可能发生
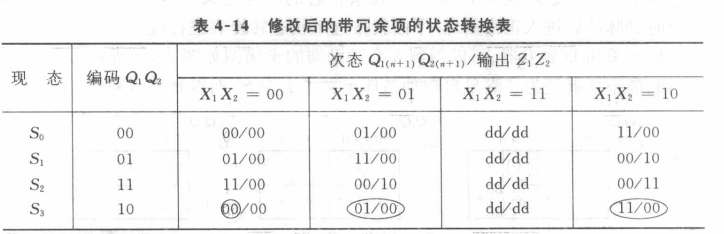
输入$X_1X_2=11$不可能发生,不做调整
eg2.
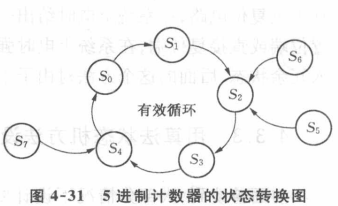
计数器冗余状态处理要求/计数器自启动条件:一旦进入冗余态,可以在有限个时钟脉冲内脱离冗余状态,进入正常计数循环
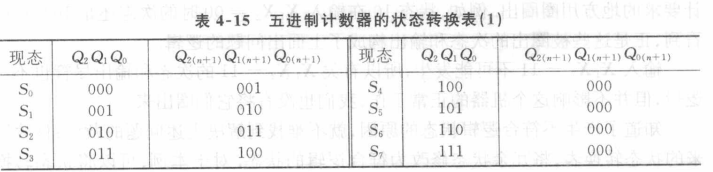
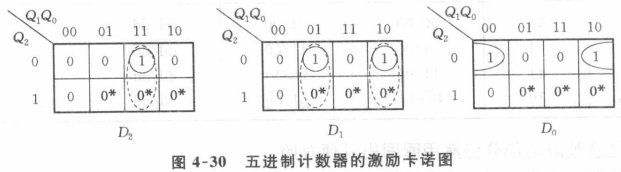
上图带(*)的最小项是为了满足自启动条件,定义次态$S_0$得到的激励值
而上图$D_2,D_1$中,3个卡诺图只有一个最小项,是3输入端与门。
卡诺圈大一点就可以减少输入端,横着不行,竖着的虚线可以!圈了冗余项得到下表

本题和售货机不同,冗余态输入输出不必满足问题特定要求,只要满足自启动就可以
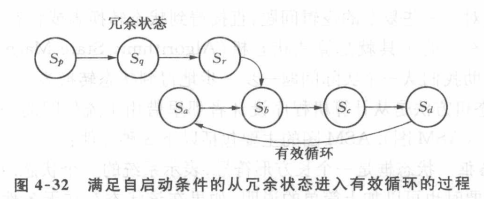
只要系统没有限制进入有效循环的实际,经过多个冗余状态再进入有效循环也是可以的
【几个有冗余状态的时序电路设计的结论】
(1)有n个状态的同步时序电路,n不是恰好等于$2^m$,总有$p=2^m-n$个冗余状态
(2)问题要求冗余态有特定输出和次态,开始设计时就要考虑进状态转换表/图
(3)只要求满足自启动条件,可以用任意项处理冗余状态。但要自启动检测,发现有问题后重新设计。
ps:复杂数字系统中,可以设计上电复位电路,在系统上电时给出复位脉冲(接到触发器直接置位/复位端,强迫状态机进入规定状态,避免系统进入冗余状态)。但此法对干扰没办法。
3 算法状态机方法
算法状态机ASM包含的元件:
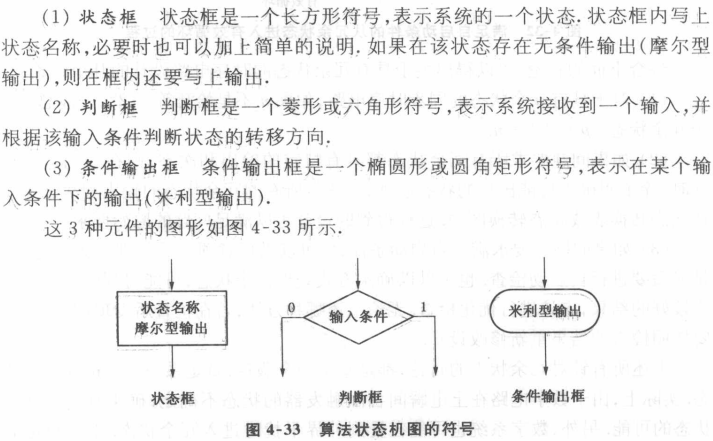
(1)状态框
(2)判断框
(3)条件输出框
还是那个例子:
自动售货机:可投1元或5角,饮料1.5元一杯,多了要找零(投2元找5角)
需要完成的功能:①记忆已投入的硬币数量
②根据硬币的数量确定是否送饮料和找零
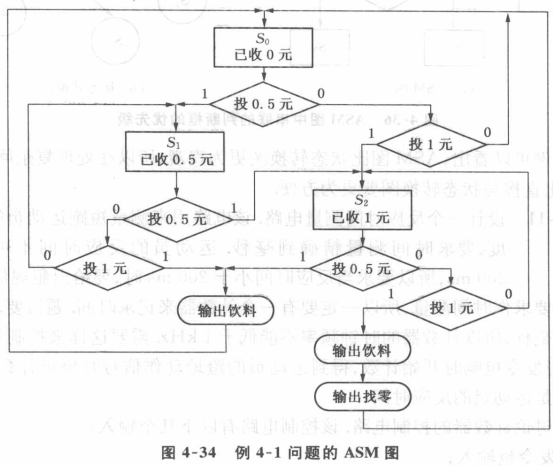
由上图得到下图
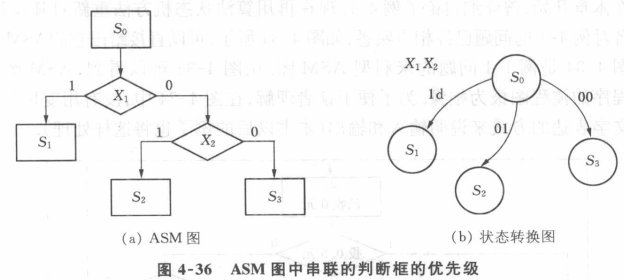
复杂问题用ASM
eg.
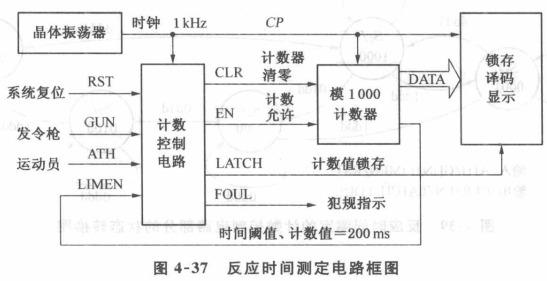
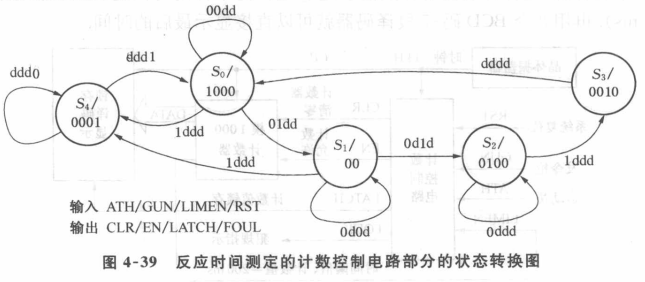
时间策略→计数器
精确到毫秒→时钟频率不低于1kHz(3个10进制计数器串联10*10*10,计数值为以毫秒为单位的BCD码,最大999ms)
计数控制:枪响→开始计数,得蹬地动作信号→停止计数,反应时间→计数值(3个BCD码-7段译码器显示最后的时间)
①输入

②输出

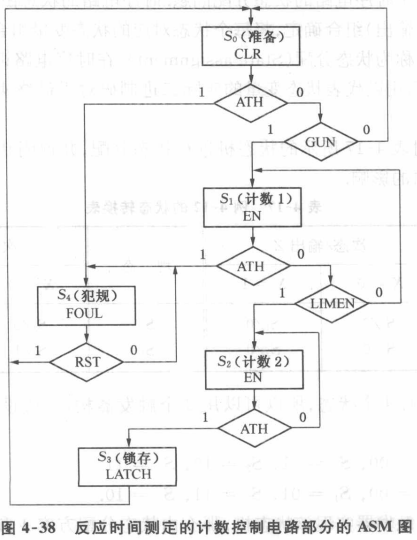
4 状态分配问题


