时序电路的描述之米利模型、摩尔模型、状态转换图、状态转换表、两种基本模型的转换
时序逻辑电路:有记忆功能,输出不仅取决于当前的输入,还与信号历史有关的一类电路
同步时序逻辑电路:
①状态变化在一个统一的内部时钟信号下发生
②系统工作按时钟节拍进行(故又叫时钟驱动时序电路)
异步时序逻辑电路:
①状态变化在外部输入信号时发生
②系统工作由外部事件驱动(故又叫事件驱动时序电路)
【本文对时序电路的描述、状态化简等基本适用异步时序电路】
1 两种基本模型
时序电路状态:记忆单元的输出逻辑组合
时序电路基本框图如下
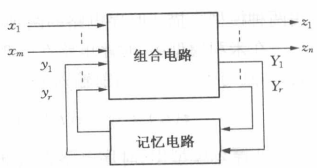
$x_1$~$x_m$:电路的m个输入变量
$z_1$~$z_n$:电路的n个输出变量
$y_1$~$y_r$:记忆电路的r个输出(状态变量)
$Y_1$~$Y_r$:记忆电路的r个输入
【引入时间概念】
时序电路的定时单位:两次驱动的间隔时间
当前时刻:某个间隔时刻$t_k$
次时刻:下一个间隔时刻$t_{k+1}$
当前时刻和次时刻的分界:驱动信号到来时刻

时序电路某当前时刻$t_k$内

$x_1$~$x_m$:$t_k$时刻的当前输入
$z_1$~$z_n$:$t_k$时刻的当前输出
$y_1$~$y_r$:$t_k$时刻记忆电路的输出,是$t_k$的现态
$Y_1$~$Y_r$:$t_k$时刻记忆电路的输入,是$t_{k+1}$次时刻记忆电路的输出
$y_i(t_{k+1})=Y_i(t_k)$
$t_k$时刻,$Y_1~Y_r$是时序电路的次态
时序电路的状态方程:$Y(t_k)=f_1[x(t_k),y(t_k)]$
($Y(t_k)$:电路在$t_k$时刻的次态)
时序电路的输出方程:$z(t_k)=f_2[x(t_k),y(t_k)]$
($z(t_k)$:电路在$t_k$时刻的当前输出)
$x(t_k)$:电路在$t_k$时刻的当前输入
$y(t_k)$:电路在$t_k$时刻的现态
【米利模型】$z(t_k)=f_1[$$x(t_k)$$,y(t_k)]$,$Y(t_k)=f_2[x(t_k),y(t_k)]$

【摩尔模型】$z(t_k)=f_1[y(t_k)]$,$Y(t_k)=f_2[x(t_k),y(t_k)]$
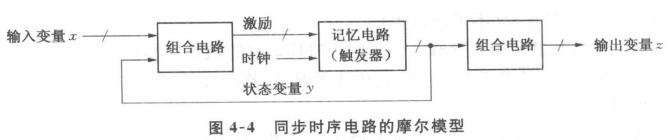
区别在于$t_k$时刻的输出$z(t_k)$是否包含$x(t_k)$
2 状态转换图、状态转换表
自动售货机:可投1元或5角,饮料1.5元一杯,多了要找零(投2元找5角)
需要完成的功能:①记忆已投入的硬币数量
②根据硬币的数量确定是否送饮料和找零
【1】米利模型
step1 输出状态(饮料、找零)
$Z_1=1$:输出饮料
$Z_2=1$:输出找零
所有输出:$Z_1Z_2=00,Z_1Z_2=10,Z_1Z_2=11$
step2 系统状态(记忆已投入硬币币值,最多只需记忆1元)
$S_0$:已投入0元
$S_1$:已投入5角
$S_2$:已投入1元
step3 输入状态(投入0元、5角、1元)
$X_1X_2=00$:投0元
$X_1X_2=01$:投5角
$X_1X_2=10$:投1元
$X_1X_2=11$:不可能发生
step4 机器动作过程(同步时序电路中所有系统状态的变化或保持→在某个时钟脉冲驱动下动作)
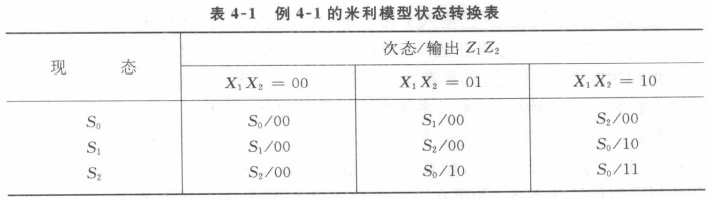
①$S_0$:已投入0元
$X_1X_2=00$:投0元,保持
$X_1X_2=01$:投5角,进入$S_1$
$X_1X_2=10$:投1元,进入$S_2$
②$S_1$:已投入5角
$X_1X_2=00$:投0元,保持
$X_1X_2=01$:投5角,进入$S_2$
$X_1X_2=10$:投1元,输出$Z_1Z_2=10$,次时刻回到$S_0$
③$S_2$:已投入1元
$X_1X_2=00$:投0元,保持
$X_1X_2=01$:投5角,输出$Z_1Z_2=10$,次时刻回到$S_0$
$X_1X_2=10$:投1元,输出$Z_1Z_2=11$,次时刻回到$S_0$
状态转换图(不适合状态个数多的复杂电路)
当前输入/当前输出 ($X_1X_2/Z_1Z_2$)
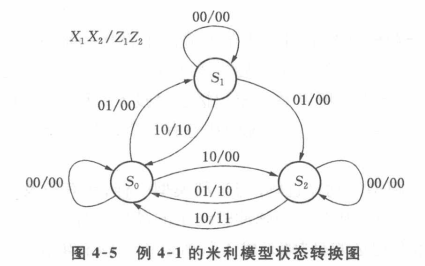
"当前":状态转换线上标注输入/输出时刻=状态转换线流出状态的时刻
eg.当前时刻$t_k$系统在$S_2$,发生输入$X_1X_2=10$,$t_k$时刻输出$Z_1Z_2=11$,下一时刻$t_{k+1}$系统状态$S_0$
状态转换表(适合状态个数多的复杂电路,可简洁地描述状态间转换关系)
【2】摩尔模型
输出不直接和输入相关,仅同系统状态有关
摩尔模型动作过程,所有论及系统状态的变化或保持,都应该理解成某个时钟脉冲驱动下的动作
$S_0$:尚未输入
$S_1$:已输入5角
$S_2$:已输入1元
$S_3$:已输入1元5角
$S_4$:已输入2元

$X_1X_2=00$无输入,$X_1X_2=01$输入5角,$X_1X_2=10$输入1元
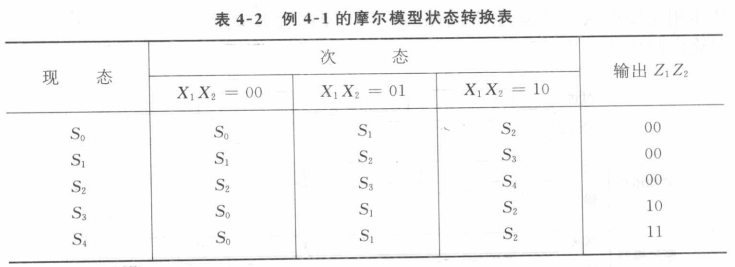
【总结】系统状态特点
①状态转换图:每个状态射出的状态转换线数=系统输入的组合数,且转换条件包含所有输入组合。(可用来检查状态转换图的正确与否)
②摩尔模型(一个状态对应一个输出)状态数$\geq $米利模型(一个状态对应多个输出)状态数
3 两种模型的基本转换
无论用何种模型描述一个问题,相同的输入序列应得到相同的输出
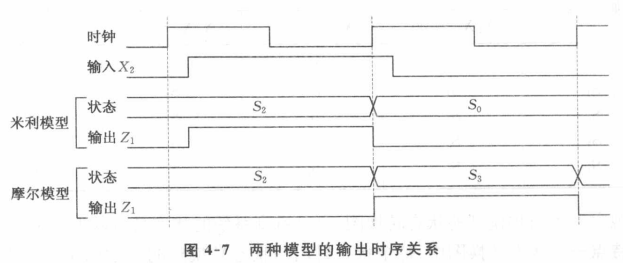
【两模型输出区别】
1.米利模型比摩尔模型提前一个时刻输出
2.摩尔模型输出在整个状态保持期间保持,米利模型由输入情况确定输出起始
3.输入有干扰,一般不影响摩尔模型输出,但会影响米利模型输出
【摩尔模型→米利模型】
(1)去掉摩尔模型状态转换表最后一列
(2)每个次态后加上输出(输出为该次态在原模型中输出)
(3)检查修改后的状态转换表,合并相同状态(去重)

本例中$S_3,S_4$在所有输入组合情况下次态和输出与$S_0$一样,故$S_0,S_3,S_4$可合并
【米利模型→摩尔模型】
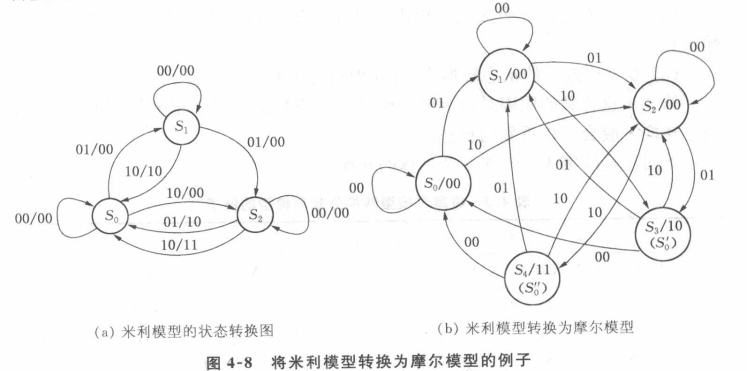
关键:找到在米利模型中不出现的次态
米利模型中的状态可分为两类:
①输出同类状态:所有指向该状态的状态转换线有相同输出。
(可直接把所有指向该状态的状态转换线上输出,改写至表示状态的圆圈中)
②非同类状态:指向该状态的状态转换线有几个不同输出。
改写步骤:
a.指向输出非同类状态的状态转换线有几个不同输出,就把这个状态分成几个新状态;
一个新状态对应一个输出,写在表示新状态的圆圈中。
b.按不同输出,把原来状态转换线改成指向对应输出的新状态。
c.原来从输出非同类状态出发的所有状态转换线,在新状态中重新画出,其目的状态和原来一样。

