机器学作业知识点复习
1.机器学习分类:监督学习、无监督学习、强化学习、半监督学习、主动学习
①监督学习:从标注数据中学习预测模型
②无监督学习:从无标注数据中学习预测模型
③强化学习:智能系统在与环境的连续互动中学习最优策略的模型
④半监督学习:从标注数据和无标注数据中学习预测模型
⑤主动学习:机器不断给实例让教师标注,再在标注数据中学习预测模型
2.机器学习涉及的要素为模型、策略和算法
(1)模型
监督学习中模型是要学习的条件概率或决策函数
模型的假设空间:包含所有可能的条件概率分布或决策函数
非概率模型:由决策函数表示的模型
概率模型:由条件概率表示的模型
(2)策略
按照什么准则学习或选择最优模型
①损失函数loss或代价cost函数(度量模型一次预测的好坏)和风险函数risk或期望expected函数(度量平均意义下模型预测的好坏),后者是前者的期望
②经验风险最小化ERM(认为经验风险最小的模型是最优模型)和结构风险最小化SRM(防止过拟合,等价于正则化)
(3)算法
学习模型的具体计算方法
统计学习的过程:基于训练数据集,根据学习策略,从假设空间中选最优模型,最后考虑求解最优模型的计算方法。
统计学习问题→最优化问题
统计学习算法→求解最优化问题的算法
①最优化问题有显式解析解,求解该最优化问题比较简单
②最优化问题不存在解析解,需要用数值计算方法求解
而如何找到全局最优解,同时求解过程比较高效也非常重要
3.用二次函数拟合数据点(x,y),并用最大似然估计求系数,并计算拟合残差
二次函数$f(x,w)=w_2x^2+w_1x+w_0$
最大似然估计系数$w=arg{min}_w\sum (y-f(x,w))^2$
上面损失函数对$w$求导等于0解出$w$就好啦
剩下的一些tricks是,首先求导是需要运用链式法则,也就是$f(x,w)$也要对$w$求导乘在后面
其次是可以利用矩阵表示方程组,同时考虑需要求的$w_2,w_1,w_0$可以放在一个向量里面,是线性方程组的变量
然后有一些含$x$的各种和的常数是线性方程组的系数矩阵
再把方程组等号右边的含$x,y$的常系数放进系数矩阵就变成增广矩阵
最后写出做初等变换后的线性方程组,再求解,就可以求出所需要的系数了
(求解例子中概念不清楚可以看 §1 线性方程组的解法 - 山大人孔乙己的文章 - 知乎 https://zhuanlan.zhihu.com/p/202713223)
求解线性方程组的例子如下
$\left\{ \begin{aligned}x_1+3x_2+x_3&=2&①\space\\ 3x_1+4x_2+2x_3&=9&②\space\\ -x_1-5x_2+4x_3&=10&③\space\\ 2x_1+7x_2 +x_3&=1 &④\space\end{aligned} \right.$
增广矩阵
$\begin{pmatrix} 1&3&1&2\\ 3&4&2&9\\ -1&-5&4&10\\ 2&7&3&1 \end{pmatrix}$
step1 消去$x_1$(将①依次乘某些系数,与②③④相加)得$\begin{pmatrix} 1&3&1&2\\ 0&-5&-1&3\\ 0&-2&5&12\\ 0&1&-1&3 \end{pmatrix}$
step2 ②④互换得$\begin{pmatrix} 1&3&1&2\\ 0&1&-1&3\\ 0&-2&5&12\\ 0&-5&-1&3 \end{pmatrix}$
step3 消去$x_2$(②依次乘某些系数,与③④相加)$\begin{pmatrix} 1&3&1&2\\ 0&1&-1&3\\ 0&0&3&6\\ 0&0&-6&-12 \end{pmatrix}$
step4 将③代入④ $\begin{pmatrix} 1&3&1&2\\ 0&1&-1&3\\ 0&0&3&6\\ 0&0&0&0 \end{pmatrix}$
step5 继续化简为行最简型$\begin{pmatrix} 1&0&0&-15\\ 0&1&0&-1\\ 0&0&1&2\\ 0&0&0&0 \end{pmatrix}$
得到$\left\{\begin{matrix} &x_1=&-15\\ &x_2=&-1\\& x_3=&2 \end{matrix}\right.$
记住这里要计算的拟合残差是每个(x,y)都有一个残差!而不是只有一个总的残差
4.用二次函数拟合数据点(x,y),其中y观测值服从高斯分布(0,$\sigma _1$),用最大后验准则求系数,其中系数满足正态分布(0,$\sigma _2$)
二次函数$f(x,w)=w_2x^2+w_1x+w_0$
最大后验准则$\displaystyle{w=arg{min}_w ln(exp(-\frac{w^2}{2\sigma _1 ^2})\prod exp(-\frac{(y-f(x,w))^2}{2\sigma _2 ^2}))}=arg{min}_w -\frac{w^2}{2\sigma _1 ^2}-\frac{(y-f(x,w))^2}{2\sigma _2 ^2}$
对$argmin$后面的式子求导,令其等于0,用与上题同样的方法求解$w$即可
结果的不同之处在于系数矩阵对角线处会加上一个和$\sigma _1$和$\sigma _2$相关的常数项
5.画计算图,用链式法则计算梯度
计算图是高效计算梯度的方法,特别适合f比较复杂的情况
计算图理论:用图的形式表达复杂的、多层的运算,其中边是变量(比如标量、矢量、矩阵和张量),而边则代表运算。
利用计算图理论可以反向求梯度
若$f(x)=\sqrt{x^2+exp(x^2)}+cos(x^2+exp(x^2))$
则设置一些中间变量如下:
$a=x^2$
$b=exp(a)$
$c=a+b$
$d=\sqrt{(c)}$
$e=cos(c)$
$f=d+e$
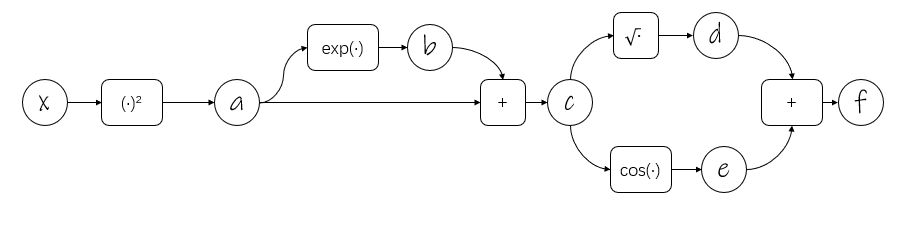
就是用链式法则把f一层一层剥开,你明白我的意思吗(微笑.jpg)
6.矢量微积分的公式及其证明
就证明而言,先让所有向量都是列向量是做此类证明题的基础。
然后可以运用矩阵的运算方法先把分子的向量乘积展开,再展开分母的分量,最后可以得到求偏导的结果,再整理成向量即可

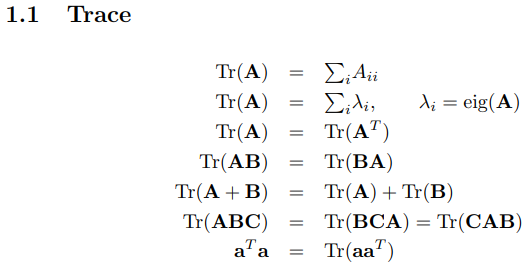

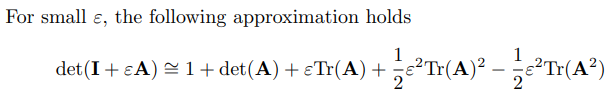


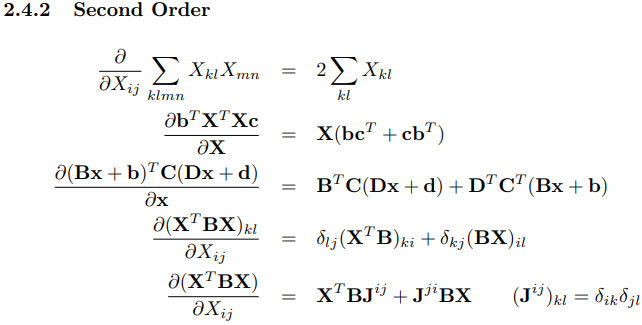
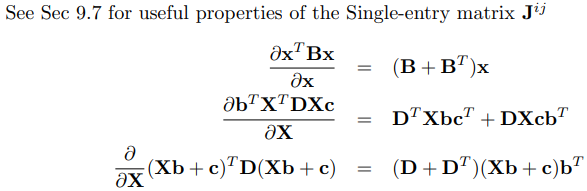
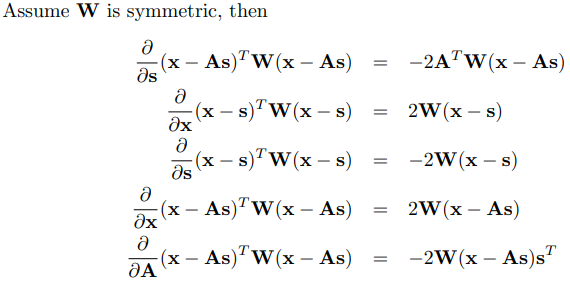

6.感知机权重的学习过程
当然可以直接代入$z=sgn(w_1x+w_2y+b)$
求出$z$和数据集里的是否相同,不相同就用w的更新公式$w=w+\eta xz$,其中$\eta $是步长
如果比较复杂的话,不如先写出空间一点到超平面的距离公式,然后写出误分类公式$-z(w_1x+w_2y+b) \geq 0$,得到误分类集,用它来更新w
7.LDA算法的降维计算过程
到今天才理解LDA算法的具体含义,我对题目的理解有错,凭什么作业可以拿A?
(我就知道自己做,没有参考答案很难做对,所以像我这样的人是不是不适合做研究)
所以助教是在可怜我吗哈哈哈哈哈!!!!
但是另一门实验课的助教可就没有可怜我们啦!属于是笨蛋上了一个不是自己等级的学校(小心捧杀哦),是不是该想想怎么蒙混过关吧……
LDA算法是一种降维算法,如果题目给出了一组有数据点,其中x是二维向量,y是分类的类别,那么LDA将降低x维度,把它从二维变成一维。
具体做法:以二分类(y=0,1),二属性(x二维)数据为例
①根据题目数据点求得两类x的两个属性的平均值,分别得到两类的数据中心μ0和μ1
②分别求两类的协方差矩阵Σ0=∑(x-μ0)(x-μ0)^T,Σ1=∑(x-μ1)(x-μ1)^T
③类内散度Sw=Σ0+Σ1(因为两个协方差矩阵都是自己类数据点和自己类中心的距离,所以叫类内)
④类间散度Sb=(μ0-μ1)(μ0-μ1)^T(因为这是在计算两类中心点的距离)
⑤(因为我们要最大化不同类投影数据点的距离,最小化同类投影数据点间的距离,所以这里有一个最优化问题详见周志华机器学习书p61-62,这里只写出求w的步骤)
经过最优化后w=Sw^(-1)(μ0-μ1)
(1)求逆矩阵Sw^(-1)之手算法,但还是推荐用代码算哈
$A=\begin{pmatrix}a & b \\\\c & d\end{pmatrix} 求A^{-1}$
$A^{-1}=\frac{1}{ad-bc}\begin{pmatrix}d& -b\\\\-c& a\end{pmatrix} $
$=\begin{pmatrix}\dfrac{d}{ad-bc} & -\dfrac{b}{ad-bc} \\\\-\dfrac{c}{ad-bc} & \dfrac{a}{ad-bc} \end{pmatrix}$
(2)求得投影方向w,然后归一化/标准化/变成单位向量一下(得到w是一个分量都不超过1的列向量)
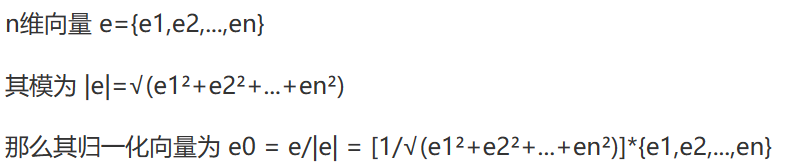
1.归一化:将训练集中某一列数值特征的值缩放到0和1之间
$X_{norm}=\frac{X-X_{min}}{X_{max}-X_{min}} \\$
2.标准化:将训练集中某一列数值特征的值缩放成均值为0,方差为1的状态
$X_{std} = \frac{X-\mu}{\sigma} \\$
w^T·x,其中w^T变成行向量(1*2),x依然是列向量(2*1)
最后结果是(1*1)的一个值,这样就做到了对x降维
8.证明迭代收敛条件的方法
我的做法是查很多资料然后找到一些高阶的最优化知识,然后抄抄算算,感觉自己写出来了……(看起来助教并没有打勾)
只能说也许不需要特别高阶的知识,可以尝试用高中的方法就可以证明收敛
什么是收敛呢,就是随着自变量的增大,你的因变量不再发生变化,稳定在一个数了
求收敛条件,就是消去会导致因变量变化的那些因素
若迭代条件X(i+1)=Xi-αf'(x)
X(i+1)是X的下标是i+1的意思
【法1】
令迭代公式的右边为一个函数g(Xi)=Xi-αf'(Xi)
那么由收敛可以得到Xi=Xi+1也就是上式的左边,这下g(Xi)=Xi就是收敛临界点,收敛条件是|g(Xi)|<Xi
也就是|g'(Xi)|<1,解一下不等式就可以得到0<α<2*1/f''(x)
【法2】
设函数f(x)=ax^2+bx+c
f'(x)=2ax+b
X(i+1)=Xi-α(2aXi+b)=(1-2aα)Xi-αb
X(i+n)=(1-2aα)X(i+n-1)-αb=(1-2aα)(1-2aα)·X(i+n-2)-αb·(1-2aα)-αb=(1-2aα)(1-2aα)(1-2aα)·X(i+n-3)-αb·(1-2aα)(1-2aα)-αb·(1-2aα)-αb=(1-2aα)^n·X(i)-αb·[∑(k=0,n-1)(1-2aα)^k]
然后收敛的条件是(1-2aα)^n→0,[∑(i=0,n-1)(1-2aα)]→0
|1-2aα|<1即-1<1-2aα<1,故0<α<1/a
而a=f''(x)/2,故0<α<1/a=2/f''(x)
9.类别不平衡
“一对一”(One vs. One,简称OvO )、 “一对其余“(One vs. Rest,简称 OvR)和 "多对多 " (Many vs. Many ,简称 MvM).
OvR和MvM问题中,对每个类进行了相同的处理,因此拆解出的二分类任务中不平衡会相互抵消,一般不用专门处理。
但就算原始问题里,不同类别的训练样例数目相同,在用OvR、MvM策略后产生的二分类问题也会有类别不平衡的现象,此时就要采用一些处理类别不平衡问题的方法。
方法一:欠采样。去掉一些多数类里的样例,使两类样例数基本差不多。
方法二:过采样。增加一些少数类里的样例,让两类样例数差不多。
方法三:阈值移动。因为判断的依据是y/(1-y)和1的大小关系,而这是正例/反例数;
因此可以先用数据训练,再在最后判断的时候,依然采取正例比负例,
但是比较的阈值不再是1(或阈值y/(1-y)),而是将其用反例/正例放缩或阈值移动一下,再用新的阈值判断即可。
10.支持向量机里的SMO算法
从支持向量机开始复习
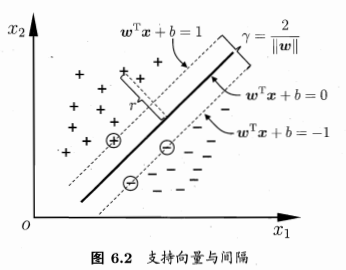
γ是间隔,来自划分超平面(专门用来划分两类样本,在其上是正例,其下是负例 btw想到了线性规划)
该超平面的位置由与距离它最近的正例和负例(各一个)决定,并与它们之间的距离相同(所以在点到直线的距离上有个二倍)
要得到最佳超平面就要最大化这个γ
换言之是最小化(1/2)*||w||2(这是为了方便计算)
下面是基本SVM模型
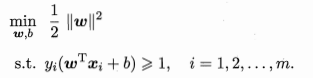
进行一些最优化变形(拉格朗日乘子法啦)
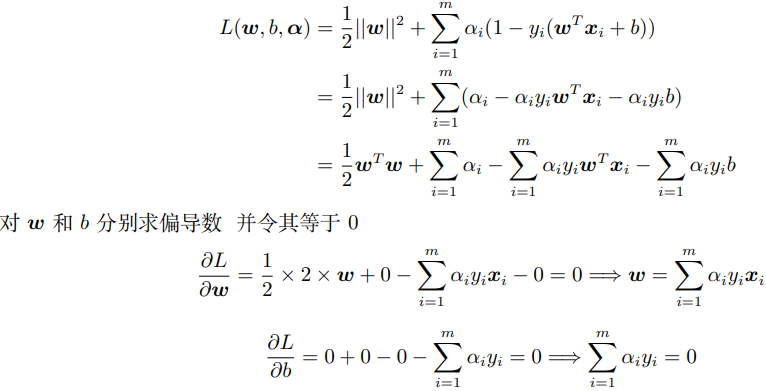
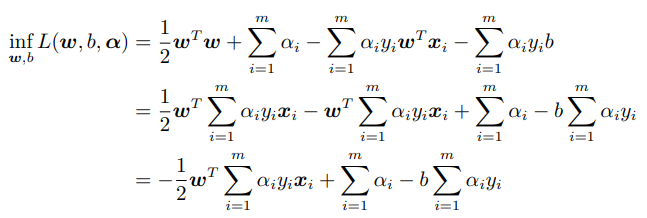

KKT条件(对于强对偶性成立的优化问题,其主问题的最优解一定满足KKT 条件)
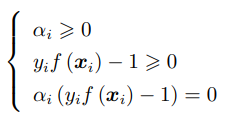
于是如何求解下面的问题(也就是求解λ)呢?【\SMO算法/,\SMO算法/(\XXX/是欢呼的意思】

方法是利用约束∑αy=0,固定除两个选定λ外其他所有λ
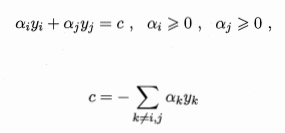
再消去αj,剩下只有αi的二次规划,然后用李航《统计学习方法》里的做法求解析解就可以了(但它那个算法真的超级超级复杂,x1·x2是核函数啦,这样或许可以简化一点)
我的同学但凡写了这道题,无论何种表达形式,用什么字母代替核函数,都是这个求解方法
(有的没有像李航的书里那样考虑不等式约束条件0<λ<C)
11.后验概率估计的两种策略
①判别式模型:直接对P(c|x)建模,x是观测值
②生成式模型:先对联合概率分布P(x,c)建模,再求P(c|x)
求解方法就是贝叶斯公式P(c|x)=P(x,c)/P(x)=P(x|c)*P(c)/P(x)
P(c)类先验概率,P(x|c)类条件似然
12.朴素贝叶斯分类器的求解方法
对二分类或多分类问题,先求出每一类的概率P(ci)
再在每一类的不同属性下求该属性在该类中出现的概率P(xj|ci)
最后判断方法是$P(c_i)×\prod _jP(x_j|c_i)$
然后比较一下i个概率,哪个大就属于哪类
13.超父独立依赖估计
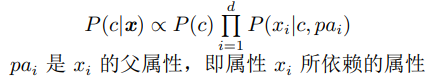
预测x为某值的情况下,y属于某类的概率怎么算?
先算y属于某类k的概率P(y=k),再求超父x_parent为某值在y属于某类k条件下的概率P(x_parent|y=k),
最后所有剩下的属性在x_parent为某值和y属于某类k的条件下,为某值的概率
14.贝叶斯网络
用贝叶斯公式就是了!!!