数据结构之迭代与递归

\(log1+log2+log3+……+logn=O(nlogn)\)
\(\displaystyle{1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+……\frac{1}{n}=O(logn)}\)
\(\displaystyle{n+\frac{n}{2}+\frac{n}{4}+\frac{n}{8}+……+1=n\frac{1−(\frac{1}{2})^{k+1}}{1−(\frac{1}{2})}=n\frac{2−(\frac{1}{2})^k}{1}=2n−\frac{n}{2^k}=2n−1}\)
How is "n+n/2+n/4....1" equal to "2n-1" using the formula for geometric series?
减而治之是与递归相关的，每经过一层递归，问题的规模都会缩小，直到最小（平凡）
原问题=子问题+平凡小问题=子问题'+\(2*\) 平凡小问题\(=……=n*\) 平凡小问题
分而治之是大问题分成小问题，但各个小问题最后组合起来又可以成为大问题
大问题\(=2*\) 小问题\(=4*\) 小问题 '\(=……=n*\) 小问题

求n数之和
①迭代方法：迭代是在上一次迭代结果的基础上继续运算，重在上一次结果
int Sum(int A[], int n){
int sum = 0; //\(O(1)\)
for(int i =0; i < n; i++)
sum += A[i]; //\(O(n)\)
return sum;} //\(O(1)\)
时间复杂度：\(O(n)\)
②递归方法：递归是自己调用自己，重在使用同样的方法
1)递归跟踪：检查每个递归实例累计所需用时（包含调用语句本身）即为算法执行时间
直观，适用于简单的递归模式
\(T(n)=O(1)*(n+1)+O(n)\)
2)递推方程
抽象，适用于复杂的递归模式
sum(A,n)
=sum(A,n-1)+A[n-1]
递归基:sum(A,0)
递推方程：
\(T(n)=T(n-1)+O(1)\)
\(T(0)=O(1)\)
求解
\(T(n)-n=T(n-1)-(n-1)=……\)
\(=T(2)-2\)
\(=T(1)-1\)
\(=T(0)\)
故
\(T(n)=O(1)+n=O(n)\)

大师定理/主定理/Master Theorem
分治策略对应的递推式的常见形式：
\(T(n)=a·T(\frac{n}{b})+O(f(n))\)
原问题=\(a\)个规模\(\frac{n}{b}\)的子任务；任务划分、解的合并耗时\(f(n)\)

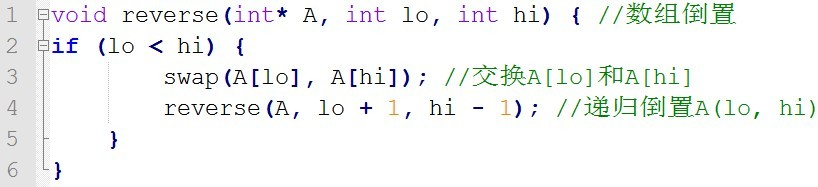
调用reverse(A, 0, n-1)，时间复杂度\(O(n)\)
下面是过程
0 1 2 …… n-3 n-2 n-1
n-1 1 2 …… n-3 n-2 0
n-1 n-2 2 …… n-3 1 0
n-1 n-2 n-3 …… 2 1 0