Logistic regression中regularization失败的解决方法探索(文末附解决后code)
在matlab中做Regularized logistic regression
原理:
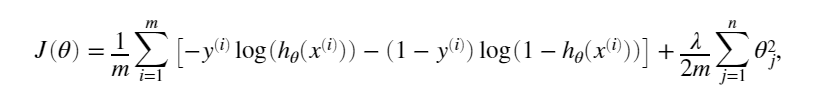
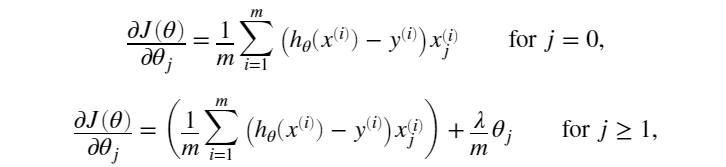
我的代码:
function [J, grad] = costFunctionReg(theta, X, y, lambda) %COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization % J = COSTFUNCTIONREG(theta, X, y, lambda) computes the cost of using % theta as the parameter for regularized logistic regression and the % gradient of the cost w.r.t. to the parameters. % Initialize some useful values m = length(y); % number of training examples % You need to return the following variables correctly J = 0; grad = zeros(size(theta)); % ====================== YOUR CODE HERE ====================== % Instructions: Compute the cost of a particular choice of theta. % You should set J to the cost. % Compute the partial derivatives and set grad to the partial % derivatives of the cost w.r.t. each parameter in theta h = sigmoid(X*theta); theta2=[0;theta(2:end)]; J_partial = sum((-y).*log(h)+(y-1).*log(1-h))./m; J_regularization= (lambda/(2*m)).*sum(theta2.^2); J = J_partial+J_regularization; grad_partial = sum((h-y).*X)/m; grad_regularization = lambda.*theta2./m; grad = grad_partial+grad_regularization; % ============================================================= end
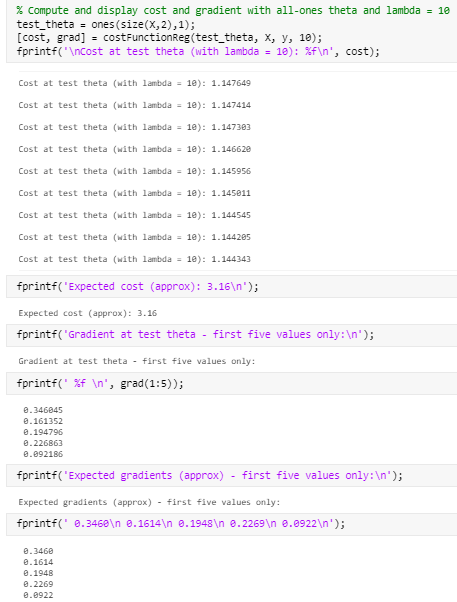
运行结果:
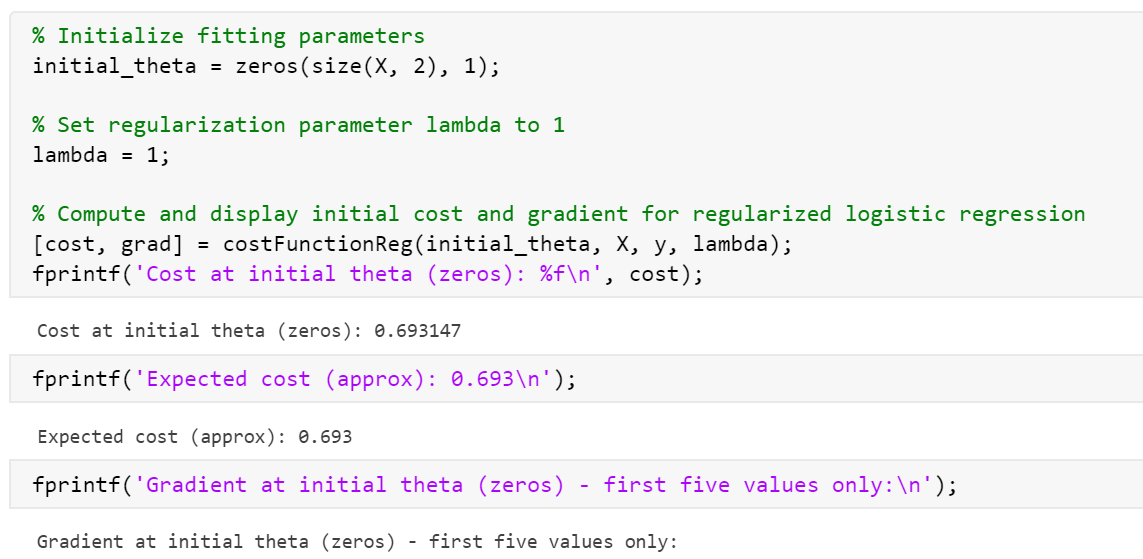

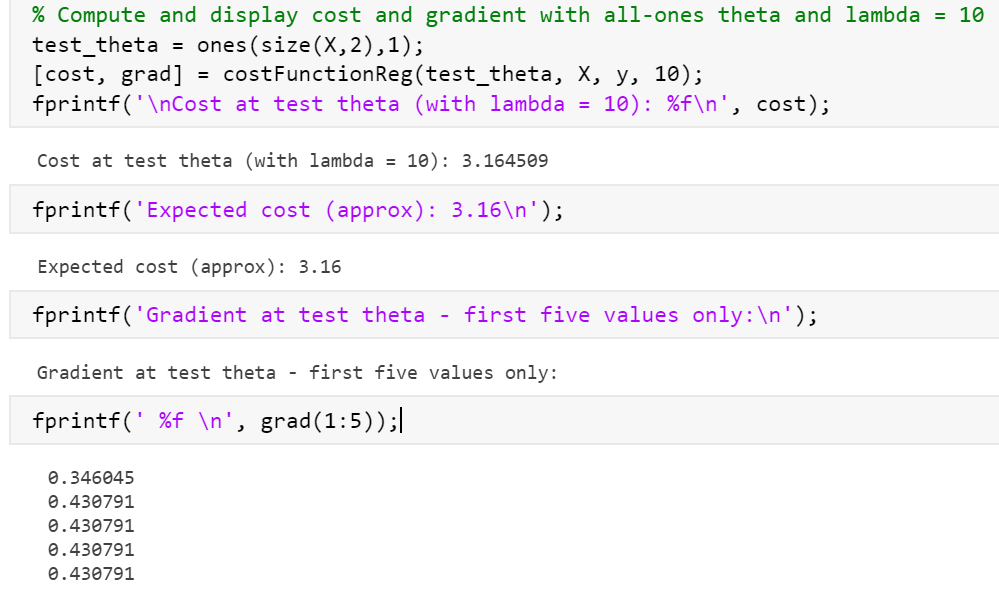

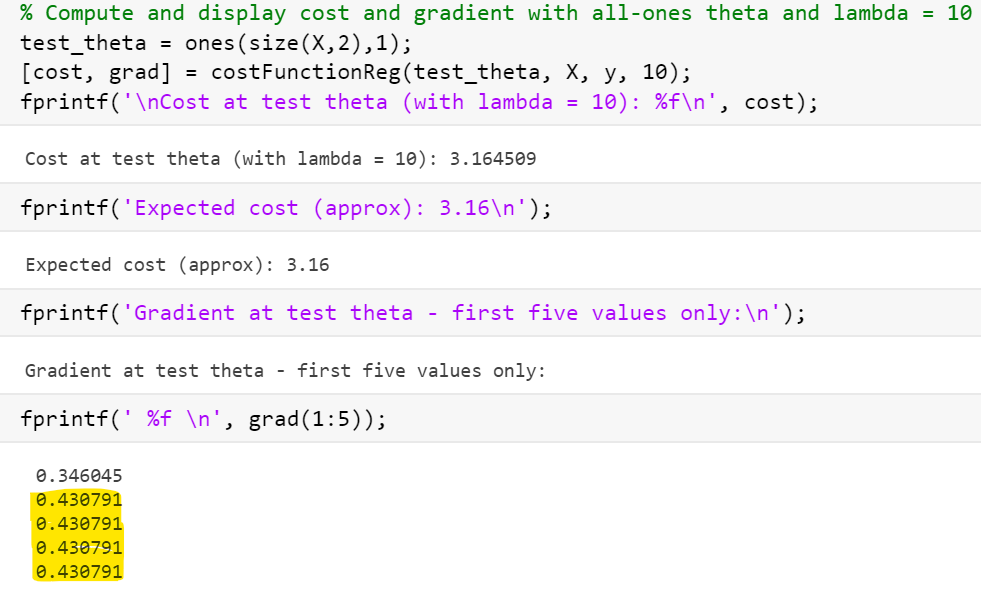
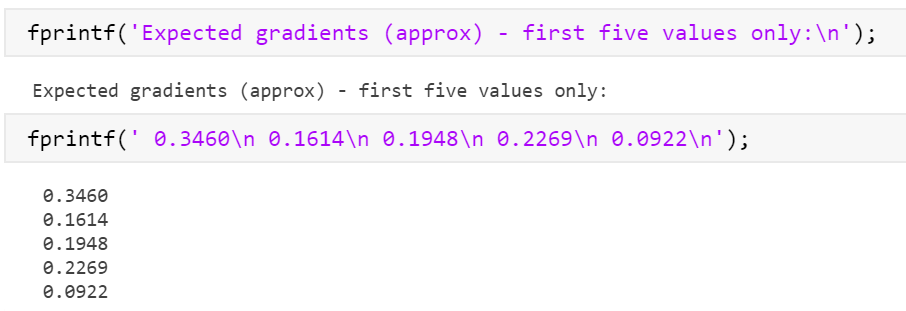
标黄的与下面的预期对比发现不同
尝试删去

部分结果符合预期,部分不符合
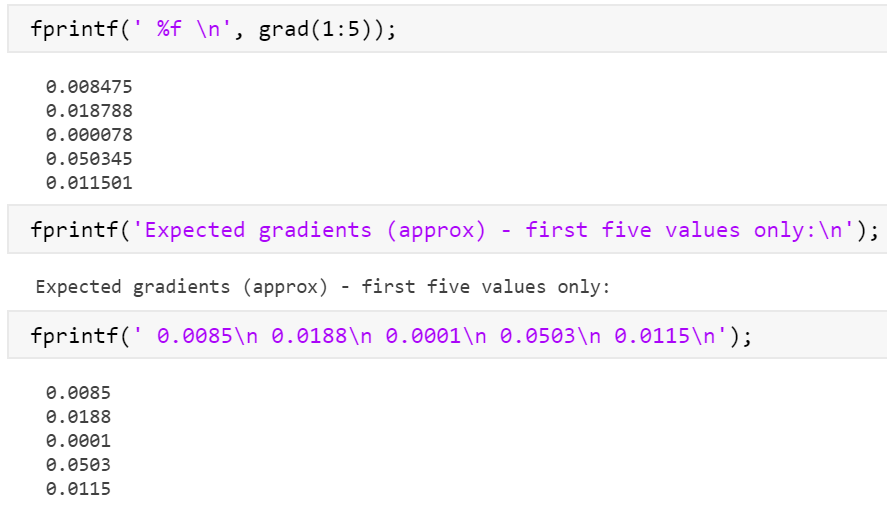
尝试大佬代码
%Hypotheses hx = sigmoid(X * theta); %%The cost without regularization J_partial = (-y' * log(hx) - (1 - y)' * log(1 - hx)) ./ m; %%Regularization Cost Added J_regularization = (lambda/(2*m)) * sum(theta(2:end).^2); %%Cost when we add regularization J = J_partial + J_regularization; %Grad without regularization grad_partial = (1/m) * (X' * (hx -y)); %%Grad Cost Added grad_regularization = (lambda/m) .* theta(2:end); grad_regularization = [0; grad_regularization]; grad = grad_partial + grad_regularization;
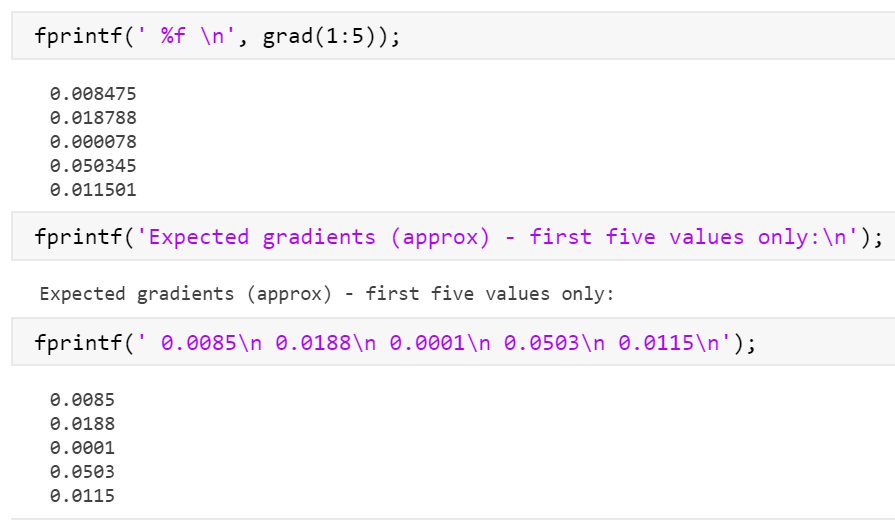
完全成功!?我不李姐……
观察大佬代码发现,我和大佬的区别在于:
最开始的theta向量和计算J(theta)和grad时候使用sum的数目
故尝试修改👉和大佬数目一样多的sum
h = sigmoid(X*theta); theta2=[0;theta(2:end)]; J_partial = (-y).*log(h)+(y-1).*log(1-h)./m; J_regularization= (lambda/(2*m)).*sum(theta2.^2); J = J_partial+J_regularization; grad_partial = (h-y).*X/m; grad_regularization = lambda.*theta2./m; grad = grad_partial+grad_regularization;
结果:incompatible不兼容

文档对该错误的解释如下

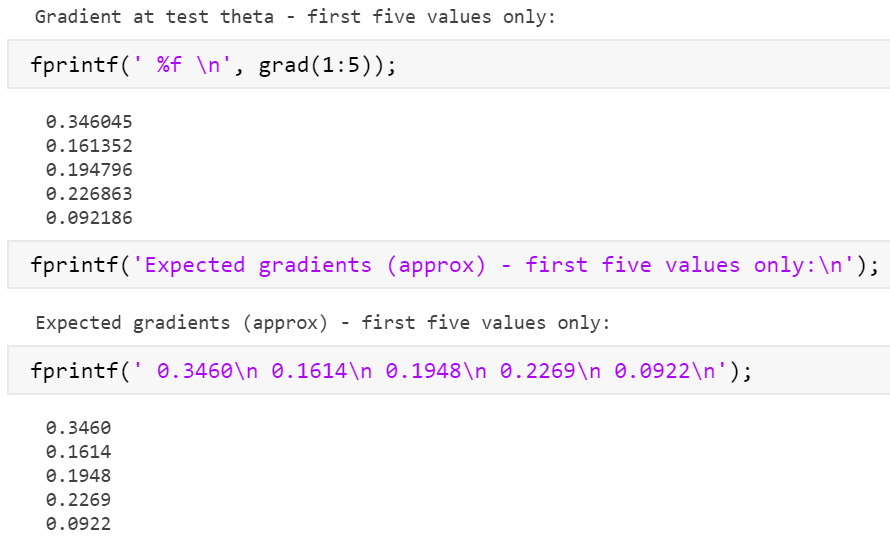
事已至此,只好向大佬更近一步!
h = sigmoid(X*theta); J_partial = (-y).*log(h)+(y-1).*log(1-h)./m; J_regularization= (lambda/(2*m)).*sum(theta(2:end).^2); J = J_partial+J_regularization; grad_partial = (h-y).*X/m; grad_regularization = lambda.*theta(2:end)./m; grad_regularization2=[0;grad_regularization]; grad = grad_partial+grad_regularization2;
为什么还是不兼容?
到底哪里出了问题?
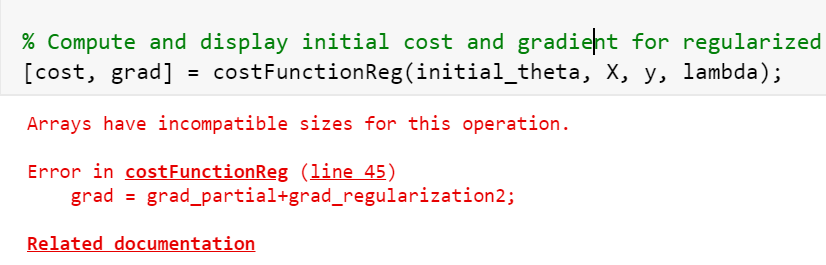
最后,尝试离大佬更近一步,把grad_partial里的(h-y).*X/m变成了(1/m) * (X' * (h -y))
h = sigmoid(X*theta); J_partial = (1/m).*((-y).*log(h)+(y-1).*log(1-h)); J_regularization= (lambda/(2*m)).*sum(theta(2:end).^2); J = J_partial+J_regularization; grad_partial = (1/m) * (X' * (h -y)); grad_regularization = (lambda/m).*theta(2:end); grad_regularization = [0; grad_regularization]; grad = grad_partial+ grad_regularization;
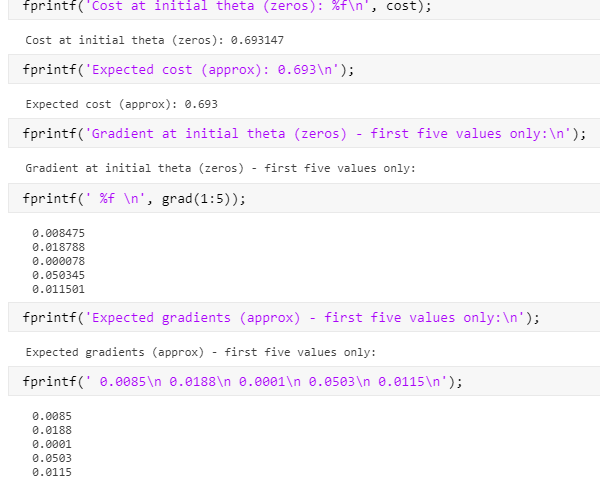
舒服了!
但,等等,上面怎么那么多行,数值还不对?看来不能完全靠大佬,还得自己改!!!
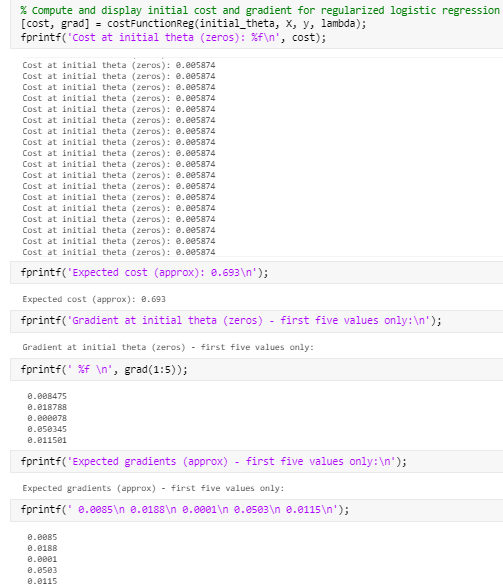
h = sigmoid(X*theta); J_partial = (1/m).*sum((-y).*log(h)+(y-1).*log(1-h)); J_regularization= (lambda/(2*m)).*sum(theta(2:end).^2); J = J_partial+J_regularization; grad_partial = (1/m) * (X' * (h -y)); grad_regularization = (lambda/m).*theta(2:end); grad_regularization = [0; grad_regularization]; grad = grad_partial+ grad_regularization;
最终,得到了满意的答案
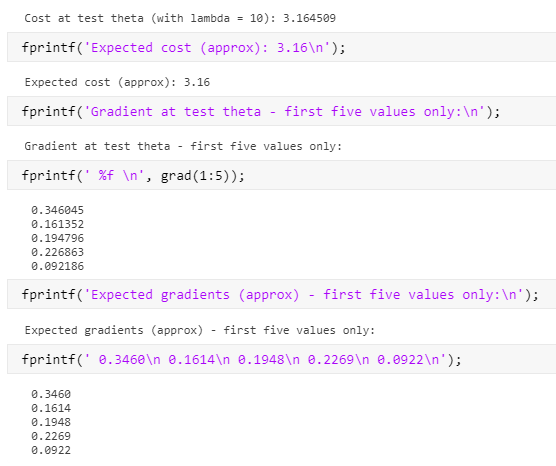
以及
总结一下出现的问题
01不兼容,就像上面说明的那样,行列不匹配
(解决方法:查看有无sum、是值还是array,把系数往前放,修改两数相乘的顺序)
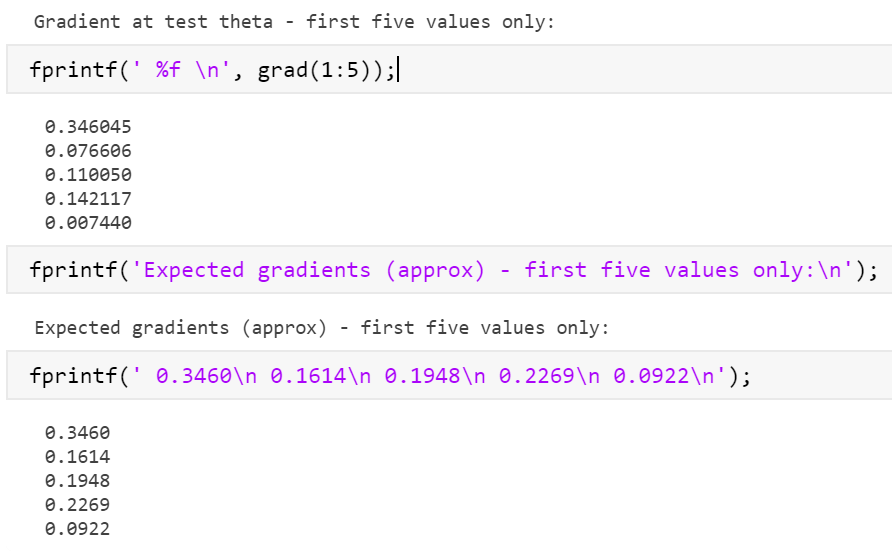
02加入grad_regularization后,grad(1,5)的后四项都出现了问题(很神奇地值相等),
一旦去掉又与正确值有小范围差距(缺少grad_regularization导致的)
说明grad_regularization存在问题
而如果一开始就将theta变为第一行元素是0的矩阵,很容易出现不兼容的问题
大佬的代码提示我们特殊情况可以分出来特殊处理,也就是:
在计算J(θ)不使用矩阵,而是用除0外、后面的θ直接产出需要的值
在计算grad时,由于输出也是矩阵,所以可以创建一个含0和其他θ的矩阵
这样既可以避免不兼容,也可以得出正确的结果
最终的部分code如下
h = sigmoid(X*theta); J_partial = (1/m).*sum((-y).*log(h)+(y-1).*log(1-h)); J_regularization= (lambda/(2*m)).*sum(theta(2:end).^2); J = J_partial+J_regularization; grad_partial = (1/m) * (X' * (h -y)); grad_regularization = (lambda/m).*theta(2:end); grad_regularization = [0; grad_regularization]; grad = grad_partial+ grad_regularization;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号