强化学习基础系列(二)：Policy Iteration， Value Iteration

0x1 强化学习基本分类

在上一篇文章中，我们介绍了强化学习的基本概念以及基本的模型定义。现在我们来对强化学习做一个基本的分类，强化学习方法，根据是否直接优化policy，可以分为value-based 方法和policy-based方法，value-based方法就是去计算状态的价值，根据价值不断优化从而推导出最优policy，而policy-based方法则直接对policy进行优化。另一种分类方法是model-free和model-based方法。

0x2 动态规划(Dynamic Programing, DP)

这种方法建立在知道MDP的转移概率和reward function的基础上进行的。动态规划方法有两种，一种是策略迭代 (policy iteration)，另一种是价值迭代 (value iteration)。

策略迭代

策略迭代分为策略评估（policy evaluatation）和策略改进（policy improvement）两步，策略评估使用bellman期望方程，对当前所采用的策略不断迭代，来获得对状态的value function，然后用策略改进，根据得到的value function来产生更优的策略，如此循环，从而得到最优策略。

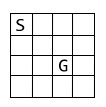
代码实现使用的环境是一个4x4的grid，在(2,2)处是terminal state，从(0,0)处出发，每走一步-1 reward。

• env code:

import numpy as np
class Grid:
    def __init__(self, width=4, height=4, goal=(2,2)):
        self.width = width
        self.height = height
        self.goal = goal
        self.move = {0:(0,1),1:(0,-1),2:(1,0),3:(-1,0)}
        #0:down 1:up 2:right 3:left
        self.pos=(0,0)
        self.done = False
        self.stepReward = -1
        self.winReward = 0

    def step(self,a):
        x,y = self.pos
        x +=  self.move[a][0]
        y += self.move[a][1]
        if self.checkLegal(x,y):
            self.pos = (x,y)
        reward = self.stepReward
        if self.pos == self.goal:
            self.done = True
            reward = self.winReward
        return  reward, self.pos, self.done 
            

    def reset(self):
        self.pos = (0,0)
        self.done = False
        return self.pos
    
    def checkLegal(self,x,y):
        return not(x < 0 or y < 0 or x >= self.width or y >= self.height)

    def render(self):
        for i in range(self.height):
            s = " "
            for j in range(self.width):
                if j == self.pos[0] and i == self.pos[1]:
                    s +='P'
                elif j == self.goal[0] and i == self.goal[1]:
                    s+='G'
                else:
                    s+='-'
            print(s)
        print(self.pos)
        print()

• policy iteration code:

import numpy as np
from env import *

def print_policy(width, height,policy,goal):
    dic={0:'D',1:'U',2:'R',3:'L'}
    for i in range(height):
        s = ""
        for j in range(width):
            if (j,i) == goal:
                s += "S"
            else:
                s += dic[policy[(j,i)]]
        print(s)
    print()

GAMMA = 0.95
EPS = 1e-3
grid = Grid()
width = grid.width
height = grid.height
policy={}
value ={}
for i in range(width):
    for j in range(height):
        if not(i == grid.goal[0] and j == grid.goal[1]):
            policy[(i,j)] = np.random.randint(4)
        value[(i,j)] = 0
cnt = 0
while True:
    while True:
        delta = 0
        for pos in policy:
            grid.pos = pos
            a = policy[pos]
            r,pos_, _ = grid.step(a)
            v = value[pos]
            v_ = r + GAMMA * value[pos_]
            value[pos] = v_
            delta = max(np.abs(v-v_),delta)
        if delta < EPS:
            break
    cnt += 1
    print("iteration: ",cnt)
    print(value)
    print_policy(width,height,policy,grid.goal)
    is_stable = True
    for pos in policy:
        max_v = float('-inf')
        max_a = 0
        for a in range(4):
            grid.pos = pos
            r,pos_,_ = grid.step(a)
            v = r + GAMMA * value[pos_]
            if max_v < v:
                max_v = v
                max_a = a
            
        if not policy[pos] == max_a:
            policy[pos] = max_a
            is_stable=False
    if is_stable:
        break

价值迭代

价值迭代则是直接根据bellman最优方程而来，每次价值函数的更新选用能采取的动作中能得到的\(\gamma V(s^{’}) + r\)中的最大值。在迭代一定程度收敛后，此时的value function已然是最优的function，直接使用 greedy策略，每次选取value function最大的作为下一步的动作。

![pseudocode of value iteration]()

• value iteration code:

import numpy as np
from env import Grid

def print_policy(width, height,policy,goal):
    dic={0:'D',1:'U',2:'R',3:'L'}
    for i in range(height):
        s = ""
        for j in range(width):
            if (j,i) == goal:
                s += "S"
            else:
                s += dic[policy[(j,i)]]
        print(s)
    print()

GAMMA = 0.95
EPS = 1e-3
grid = Grid()
width = grid.width
height = grid.height
policy={}
value ={}
for i in range(width):
    for j in range(height):
        value[(i,j)] = 0
print(value)
cnt = 0

while True:
    delta = 0
    for pos in value:
        if pos == grid.goal:
            continue
        v = value[pos]
        max_v = float('-inf')
        for a in range(4):
            grid.pos = pos
            r,pos_, _ = grid.step(a)
            v_ = r + GAMMA * value[pos_]
            max_v = max(max_v, v_)
        value[pos] = max_v
        delta = max(np.abs(v-max_v),delta)
    if delta < EPS:
        break
    cnt += 1
    print("iteration: ",cnt)
    print(value)

for pos in value:
    max_v = float('-inf')
    max_a = 0
    for a in range(4):
        grid.pos = pos
        r,pos_,_ = grid.step(a)
        v_ = r + GAMMA* value[pos_]
        if max_v < v_:
            max_v = v_
            max_a = a
    policy[pos] = max_a

print_policy(width,height,policy,grid.goal)