南理第八届校赛同步赛-C count_prime//容斥原理

大致思路就是先求出n的质因数假设是a1-an，然后在1-a的区间里面查找至少能整除{a1,a2...an}中一个元素的数有多少个，对1-b也做相同的处理，而找出来的元素肯定是与n不互质的，那么把区间的长度减去元素的个数就是那个区间里面与n互质的数的个数了，然后1-b的减去1-（a-1）的就是答案了。

而在1-a的区间里面查找至少能整除{a1,a2...an}中一个元素的数有多少个，这里就要用到容斥原理了。

首先来看容斥原理

在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

就比如质因数有2，3 然后1-10里面能整除2的有2，4，6，8，10；能整除3的有3，6，9；把这个看作成集合A，集合B，|A∩B|=1,|A|=5,|B|=3,|A∪B|=|A|+|B|-|A∩B|;

将这个公式推广到n个集合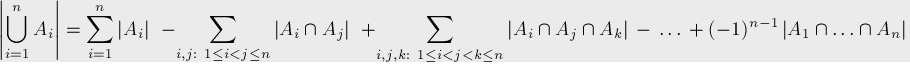

回到题目，考虑质因子{a1,a2,a3..an}，那么在[1-r]有多少个数能整除ai,答案就是[r/ai],但是单纯的把答案加上去肯定是错的（有些数可能被好几个质因子整除），这个时候就用到容斥原理来解决。

假设有m个质因子，那么就有2^m-1种情况（lcm（...)，中间填入数字，每个数字都有两种选择,填还是不填,但不能全部都不填对吧）；

附上模板

int solve (ll n, ll r)
{

        vector<ll> p;
        p.clear();
        for (int i=2; i*i<=n; ++i)
                if (n % i == 0)
                {
                    p.push_back (i);
               while (n % i == 0)
                    n /= i;
                }
               if (n > 1)
                p.push_back (n);
        //分解质因数
        ll sum = 0;
        ll cur;
        ll mult = 1;
        ll bits = 0;
        ll s=1<<p.size();
        for (ll msk=1; msk<s; msk++)
        {

              mult = 1;
               bits = 0;
                for (int i=0; i<p.size(); ++i)
                        if (msk & (1<<i))
                        {
                                bits++;
                               mult *= p[i];

                       }
               cur = r / mult;
                if (bits % 2 == 1)
                sum += cur;
               else
                sum -= cur;

        }
        //printf("%lld\n",sum);
        return r - sum;//1-r与n互质的数的个数

}

我把模板里面的位运算解释一下吧，p.size()代表n的质因数有多少个，而1<<p.size()就是2^(p.size())，mult表示某几个质因数的最小公倍数，bits表示集合的个数，用msk把1->p.size()-1里面所有的数用二进制表示出来，而if(a&b)表示a和b的二进制表示有没有相同的一位都为1，如果有就为真，没有就为假，现在假如有一个数30，那么它的质因数有2，3，5，那么一共有001，010，011，100，101，110，111，这七种情况，在里面的第二个循环其实就是为了读取msk的二进制有哪几位是1，因为二进制把所有的情况都包括了，就比如001，001&001=1，其他的都为假，这个时候就读到了｜A1｜这种情况，即2，里面的循环1<<i，只能得到001，010，100这几个数，010&010=1，其他的都为假，这个时候就读到了｜A2｜这种情况，即3，011&001＝1，011&010=1，这个时候就读取到了｜A1∩A2｜的情况，即2，3的最小公倍数即6，而由于容斥原理当里面的集合有偶数个的时候是要减去这个集合里面元素的数量的，所以这个时候就知道了｜A1｜＋｜A2｜－｜A1∩A2｜，

100&100=1，这个时候读到了｜A3｜，

101&001=1，101&100=1，这个时候读到了｜A1∩A3｜，

110&100=1，110&010=1，这个时候读到了｜A2∩A3｜，

111&001=1，111&010=1，111&100=1，这个时候读到了｜A1∩A2∩A3｜，

到这个时候所有的情况已经全部都读取完毕了，然后按照在[1-r]有多少个数能整除ai,答案就是[r/ai]这种性质，就能求出每个集合里面元素的数量，然后按照容斥原理的公式相加减就好了。

那么答案就是套模板了

#include <stdio.h>
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
vector<ll> p;
int solve (ll n, ll r)
{

        p.clear();
        for (int i=2; i*i<=n; ++i)
                if (n % i == 0)
                {
                    p.push_back (i);
               while (n % i == 0)
                    n /= i;
                }
               if (n > 1)
                p.push_back (n);
        //分解质因数
        ll sum = 0;
        ll cur;
        ll mult = 1;
        ll bits = 0;
        ll s=1<<p.size();
        for (ll msk=1; msk<s; msk++)
        {

              mult = 1;
               bits = 0;
                for (int i=0; i<p.size(); ++i)
                        if (msk & (1<<i))
                        {
                                bits++;
                               mult *= p[i];

                       }
               cur = r / mult;
                if (bits % 2 == 1)
                sum += cur;
               else
                sum -= cur;

        }
        //printf("%lld\n",sum);
        return r - sum;//1-r与n互质的数的个数

}
int main()
{
    ll a,b,n;
    int t;
    scanf("%d",&t);
   while(t--)
   {
       scanf("%lld %lld %lld",&a,&b,&n);
       ll r=solve(n,b);
       ll l=solve(n,a-1);
       printf("%lld\n",r-l);

   }
}