洛谷 P1123 取数游戏,状压dp入门(从朴素dfs到记忆化搜索,再到状压dp)
一.朴素的dfs 解法 ,回溯法
思路:每个格子有两种状态 ,选和不选, 用0和1 表示,相当于01整数规划问题
约束条件:若一个格子被选,则相邻格子不能被选
用一个 vis 数组来表示
然后逐行逐列扫描,挨个枚举,每个格子的状态,然后根据约束来剪枝
第一行的合法情况
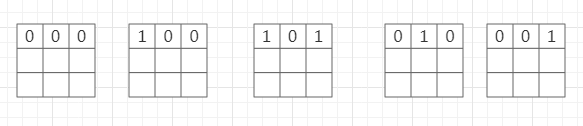
每使用一个格子,将其周围的8个格子标记为 1
比如
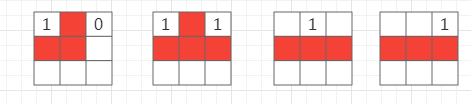
vis 标记为1 后,就不能再选
然后回溯的时候,记得恢复。
要注意,这里的vis 是可以叠加的,所以使用 +1 - 1 的操作
只有 vis=0 的才能选
搜索状态树举例子:
当第一行为 000 时 向下搜索 的情况, 其他情况 类似,依次类推
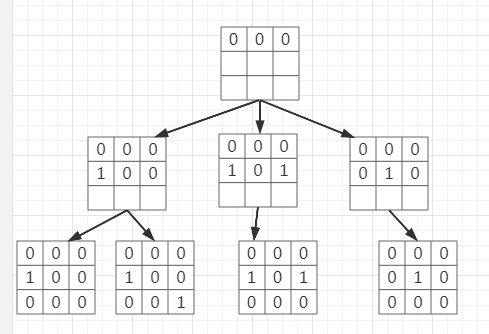
复杂度 O(2^nm)
回溯法的代码如下:
#include<iostream> #include<algorithm> using namespace std; typedef long long i64; const int MAXN = 10; int grid[MAXN][MAXN]; int vis[MAXN][MAXN]; int row,col; int t; int ans = 0; bool inArea(int x,int y){ return x>=0 && x<row && y>=0 && y<col; } //用 int ,因为可以重复添加 void setVis(int x,int y,int v){ for(int i=x-1;i<=x+1;i++){ for(int j=y-1;j<=y+1;j++){ if(inArea(i,j)){ vis[i][j] += v; } } } } void dfs(int x,int y,int sum){ if(y>=col){ y = 0; x++; } if(x>=row){ ans = max(ans,sum); return; } //选 if(!vis[x][y]){ setVis(x,y,1); dfs(x,y+1,sum+grid[x][y]); setVis(x,y,-1); } dfs(x,y+1,sum); } int main(){ cin>>t; while(t--){ cin>>row>>col; for(int i=0;i<row;i++){ for(int j=0;j<col;j++){ cin>>grid[i][j]; } } ans = 0; dfs(0,0,0); cout<<ans<<endl; } return 0; }
二.状态压缩的朴素 dfs 写法
思路和方法1 类似,只是将 visited 压入一个二进制数内,代表是否被占用
以行为决策变量,以该行的列是否被选当做状态,向下搜索
1 判断 某一行的状态是否合法
即:不能用相邻的1
将状态值,左移1位,与原状态值做与运算 即可,为0即合法,>0就是不合法
比如 1000101 合法
1010101 合法
1001100 不合法,因为用连续的1
bool checkCol(int state){ return ((state<<1)&state)==0; }
2 判断上下两行的状态是否合法
设当前位为 i , 则上一状态的第1位为1时,当前状态不能与 上一个状态的 第 i 位,i-1位,i+1位相同,即不能为1
为1 就返回 false。
比如
101
010 就不合法
101
000 就合法
bool checkNebour(int last,int cur){ for(int i=0;i<=col;i++){ if(((last>>i)&1)==1){ if(((cur>>i)&1)==1){ return false; } if(i-1>=0 && ((cur>>(i-1))&1)==1){ return false; } if(i+1<=col && ((cur>>(i+1))&1)==1){ return false; } } } return true; }
复杂度 O(*2^nm)
完整代码如下:
#include<iostream> #include<algorithm> using namespace std; typedef long long i64; const int MAXN = 10; i64 grid[MAXN][MAXN]; int row,col; int t; i64 ans = 0; bool checkCol(int state){ return ((state<<1)&state)==0; } bool checkNebour(int last,int cur){ for(int i=0;i<=col;i++){ if(((last>>i)&1)==1){ if(((cur>>i)&1)==1){ return false; } if(i-1>=0 && ((cur>>(i-1))&1)==1){ return false; } if(i+1<=col && ((cur>>(i+1))&1)==1){ return false; } } } return true; } i64 getSum(int curRow,int state){ i64 sum = 0; for(int i=0;i<col;i++){ if(((state>>i)&1)==1){ sum += grid[curRow][i]; } } return sum; } i64 dfs(int curRow,int lastState){ if(curRow>=row){ return 0; } i64 res = 0; for(int state = 0;state<(1<<col);state++){ if(lastState!=-1){ if(checkCol(state) && checkNebour(lastState,state)){ i64 s = getSum(curRow,state); res = max(res,dfs(curRow+1,state)+s); } }else{ if(checkCol(state)){ i64 s = getSum(curRow,state); res = max(res,dfs(curRow+1,state)+s); } } } return res; } int main(){ cin>>t; while(t--){ cin>>row>>col; for(int i=0;i<row;i++){ for(int j=0;j<col;j++){ cin>>grid[i][j]; } } ans = dfs(0,-1); cout<<ans<<endl; } return 0; }
三.记忆化搜索的 写法
再观察一下搜索树
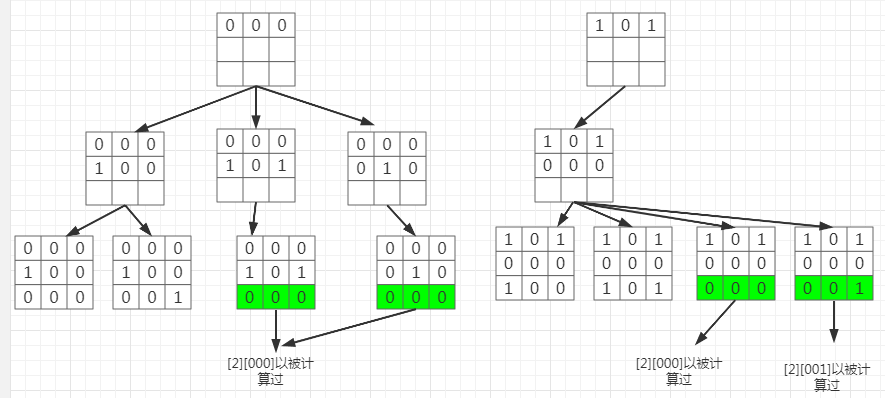
可以观察到,状态 000 ,001 之前都被计算过
所以为了防止重复计算,可以加上记忆化
mem[row][state] 来记录每行的状态,如果之前被计算过,则直接返回,反之则向下搜索
复杂度 O(n*2^m)
#include<iostream> #include<algorithm> #include<cstring> using namespace std; typedef long long i64; const int MAXN = 10; i64 grid[MAXN][MAXN]; i64 mem[MAXN][1<<MAXN]; int row,col; int t; i64 ans = 0; bool checkCol(int state){ return ((state<<1)&state)==0; } bool checkNebour(int last,int cur){ for(int i=0;i<=col;i++){ if(((last>>i)&1)==1){ if(((cur>>i)&1)==1){ return false; } if(i-1>=0 && ((cur>>(i-1))&1)==1){ return false; } if(i+1<=col && ((cur>>(i+1))&1)==1){ return false; } } } return true; } i64 getSum(int curRow,int state){ i64 sum = 0; for(int i=0;i<col;i++){ if(((state>>i)&1)==1){ sum += grid[curRow][i]; } } return sum; } i64 dfs(int curRow,int lastState){ if(curRow>=row){ return 0; } if(lastState!=-1 && mem[curRow][lastState]!=-1){ return mem[curRow][lastState]; } i64 res = 0; for(int state = 0;state<(1<<col);state++){ if(lastState!=-1){ if(checkCol(state) && checkNebour(lastState,state)){ i64 s = getSum(curRow,state); res = max(res,dfs(curRow+1,state)+s); } }else{ if(checkCol(state)){ i64 s = getSum(curRow,state); res = max(res,dfs(curRow+1,state)+s); } } } if(lastState!=-1){ mem[curRow][lastState] = res; } return res; } int main(){ cin>>t; while(t--){ cin>>row>>col; for(int i=0;i<row;i++){ for(int j=0;j<col;j++){ cin>>grid[i][j]; } } memset(mem,-1,sizeof mem); ans = dfs(0,-1); cout<<ans<<endl; } return 0; }
四.状压dp的 写法
由记忆化搜索的代码,可以演化和推导出dp的代码
因为决策变量,i 表示 行,只会向下走,且每行的状态,只依赖于上一行。
所以是可以使用动态规划来求解的。
状态定义:
dp[i][j] 代表 第 i 行,状态为 j 时的最大值
j 取值为 0~2^col , 表示该列 0 ~ col 的数有没有被选
状态计算
dp[i][state] = max(dp[i][state],dp[i-1][lastState]+s);
s表示 当前列的选了的数的和
计算方式:
枚举上一行的状态和当前行的状态,然后判断和法性,
满足约束条件的,调用状态转移方程,计算值即可
完整代码如下:
#include<iostream> #include<algorithm> #include<cstring> using namespace std; typedef long long i64; const int MAXN = 10; i64 grid[MAXN][MAXN]; i64 dp[MAXN][1<<MAXN]; int row,col; int t; i64 ans = 0; bool checkCol(int state){ return ((state<<1)&state)==0; } bool checkNebour(int last,int cur){ for(int i=0;i<=col;i++){ if(((last>>i)&1)==1){ if(((cur>>i)&1)==1){ return false; } if(i-1>=0 && ((cur>>(i-1))&1)==1){ return false; } if(i+1<=col && ((cur>>(i+1))&1)==1){ return false; } } } return true; } i64 getSum(int curRow,int state){ i64 sum = 0; for(int i=0;i<col;i++){ if(((state>>i)&1)==1){ sum += grid[curRow][i]; } } return sum; } void solve(){ memset(dp,0,sizeof dp); for(int i=0;i<row;i++){ if(i==0){ for(int state = 0;state<(1<<col);state++){ if(checkCol(state)){ i64 s = getSum(i,state); dp[i][state] = s; } } }else{ for(int lastState=0;lastState<(1<<col);lastState++){ for(int state = 0;state<(1<<col);state++){ if(checkCol(state) && checkNebour(lastState,state)){ i64 s = getSum(i,state); dp[i][state] = max(dp[i][state],dp[i-1][lastState]+s); } } } } for(int state = 0;state<(1<<col);state++){ ans = max(ans,dp[row-1][state]); } } } int main(){ cin>>t; while(t--){ cin>>row>>col; for(int i=0;i<row;i++){ for(int j=0;j<col;j++){ cin>>grid[i][j]; } } ans = 0; solve(); cout<<ans<<endl; } return 0; }
五.各种方法运行时间对比
1 回溯法 534ms
2 朴素dfs 431ms
3.记忆化搜索 26ms
4 状压dp 23ms
可见,记忆化搜索和状态压缩dp,在时间上比朴素dfs 和回溯法要快上很多



 浙公网安备 33010602011771号
浙公网安备 33010602011771号