分治法入门，自底向上，回溯和递归树后续遍历

一.利用分治法来求数组的最大值

 

以 洛谷B2057 最高的分数为例

一般的朴素做法

#include<iostream>

using namespace std;

int main(){
    int n;
    cin>>n;
    int a[n];
    int max = 0;
    for(int i=0;i<n;i++){
        cin>>a[i];
        if(a[i]>max){
            max = a[i];
        }
    }
    cout<<max<<endl;
    return 0;
}

利用分治法实现

#include<iostream>

using namespace std;

int max2(int a[],int low,int high){
    if(low>=high){
        return a[low];
    }
    int mid = (low+high)/2;
    int m1 = max2(a,low,mid);
    int m2 = max2(a,mid+1,high);
    int m3 = m1>m2?m1:m2;
    return m3;
}

int main(){
    int n;
    cin>>n;
    int a[n];
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    int m = max2(a,0,n-1);
    cout<<m<<endl;
    return 0;
}

 

二.分治法求最大值图解分析

以这个例子为例 [85 ,78 ,90, 99, 60,100,87,55]

分治的过程如下

 

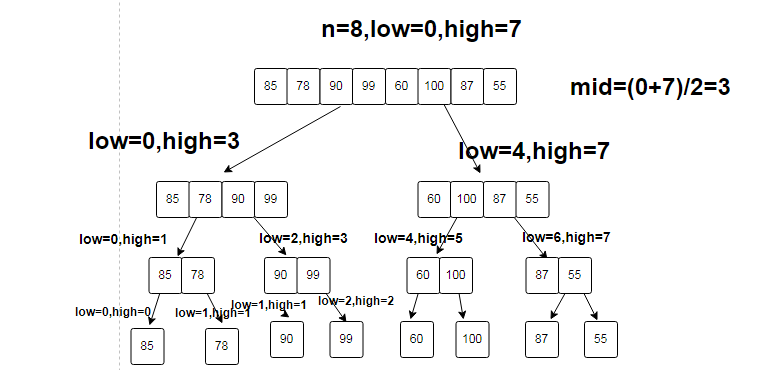
 回溯与自底向上的过程如下:

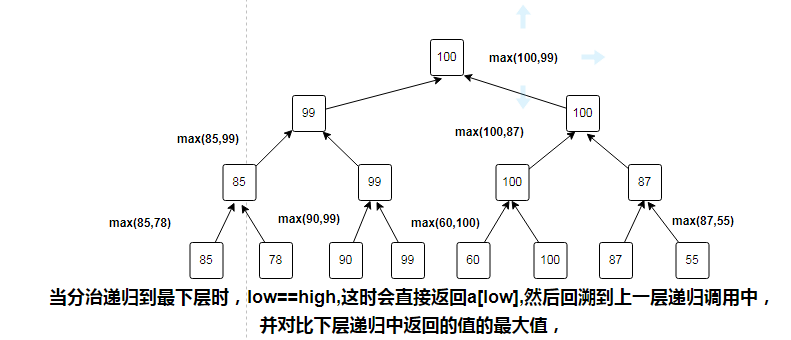
类似二叉树的后续遍历

 

三:总结

注意的点：

1.分界点的确定 

2.边界的处理，即分界点上下标的处理，防止越界和死循环，死递归暴栈。

3.注意奇偶性的判断，即考虑长度为偶数和奇数的情况。

好处：降低算法的时间复杂度

可以把一个O(n)复杂度的朴素算法，降低到O(logn)的复杂度，提高效率

但也要注意频繁的递归会带来开销，而且容易暴栈溢出。使用时要尤其注意，多跑测试用例，考虑极端数据的情况。

 

参考书籍:《算法与设计分析基础》