递归遍历二维数组,图的邻接矩阵,深度优先搜索dfs
一.递归遍历二维数组,即深度优先搜索
主要是向右,向下搜索
public class DFSTest1 { public static void main(String[] args) { int[][] a1 = new int[][]{ {1,2,3,4}, {5,6,7,8}, {9,10,11,12}, }; int row = a1.length; int col = a1[0].length; boolean[][] visited = new boolean[row][col]; dfs(a1,0,0,visited); } private static void dfs(int[][] nums,int x,int y,boolean[][] visited){ int row = nums.length; int col = nums[0].length; if(x>=row){ return; } if(y>=col){ return; } if(visited[x][y]){ return; } System.out.print(nums[x][y] +","); visited[x][y] = true; dfs(nums,x+1,y,visited); dfs(nums,x,y+1,visited); } }
输出: 1,5,9,10,11,12,6,7,8,2,3,4,
搜索方向如下图所示:
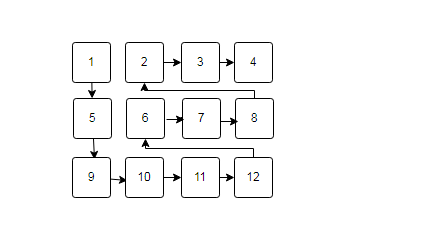
二.递归遍历图,基于邻接矩阵,即深度优先搜索
//无向无权图 public class Graph { //顶点数量 private int vertexNum; //边的数量 private int edgeNum; //邻接矩阵 private int[][] adjustMatrix; public Graph(int v){ vertexNum = v; adjustMatrix = new int[v][v]; } public boolean addEdge(int begin,int end){ if(begin<0||begin>=vertexNum||end<0||end>=vertexNum){ return false; } adjustMatrix[begin][end] = 1; adjustMatrix[end][begin] = 1; edgeNum++; return true; } public void dfs(int start, Set<Integer> visited){ System.out.println(start); visited.add(start); for (int i = 0; i < vertexNum; i++) { if(!visited.contains(i) && adjustMatrix[start][i]==1){ dfs(i,visited); } } } }
public class GraphTest { public static void main(String[] args) { Graph graph = new Graph(5); graph.addEdge(0,1); graph.addEdge(0,2); graph.addEdge(0,3); graph.addEdge(2,3); graph.addEdge(2,4); graph.addEdge(1,4); Set<Integer> visited = new HashSet<>(); graph.dfs(0,visited); } }
输出:
0
1
4
2
3
图结构 邻接矩阵
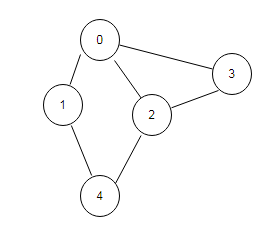

搜索过程 ,和邻接表的搜索过程类似
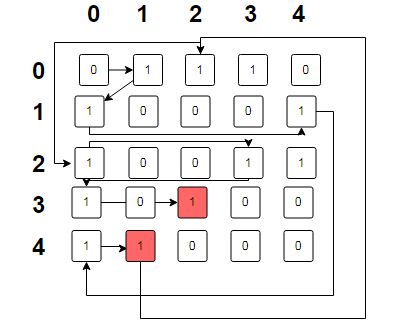
1.从 顶点0开始,即第0行开始搜索
2.搜索到第一个为 1 的,输出1,然后去 第1行搜索
3.搜索到第4个为1,输出4,去第4行查找,与4顶点相连的元素,发现没有了。
4 .从第0行 ,第2个元素开始查找,输出2,去第2行找,找到3,输出3,去第3行找与3顶点相连的顶点
发现没有了,即不满足条件,结束。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号