递归遍历各种数据结构,深入理解前序遍历,后续遍历,深度优先dfs。
一.递归遍历数组
public class Graph4Test { public static void main(String[] args) { int[] a1 = new int[]{1,2,3,4,5,6}; preOrder(a1,0); System.out.println(); postOrder(a1,0); } //前序遍历 private static void preOrder(int[] a,int pos) {
//递归退出条件 ,即当前索引下标值 > 数组的length if(a.length-1<pos){ return; } System.out.print(a[pos]+","); preOrder(a,pos+1); } //后续遍历 private static void postOrder(int[] a,int pos) { if(a.length-1<pos){ return; } postOrder(a,pos+1); System.out.print(a[pos]+","); } }
输出:
1,2,3,4,5,6,
6,5,4,3,2,1,
前序遍历调用
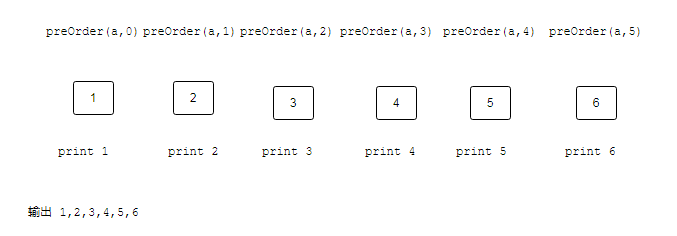
后序遍历调用,后序遍历的话,是先一直递归查找到最后一个元素,才开始调用打印,所以是从后往前打印
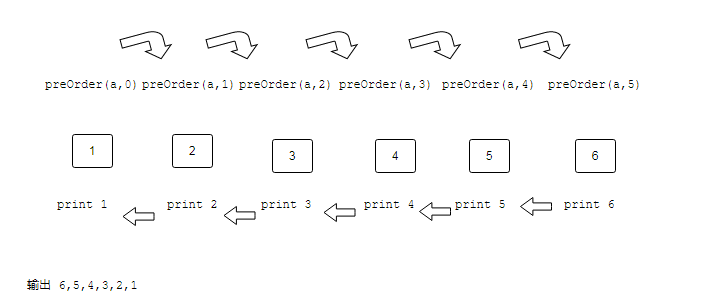
二.递归遍历链表
链表的递归遍历同数组的一样
public class ListTest1 { public static void main(String[] args) { ListNode l1 = LinkListUtil.geneLinkList(new int[]{1,2,3,4,5,6}); preOrder(l1); System.out.println(); postOrder(l1); } //前序遍历 private static void preOrder(ListNode l){
//递归的退出条件,指向链表的当前指针为空 if(l==null){ return; } System.out.print(l.getVal()+","); preOrder(l.getNext()); } //后序遍历 private static void postOrder(ListNode l){ if(l==null){ return; } postOrder(l.getNext()); System.out.print(l.getVal()+","); } }
输出:
1,2,3,4,5,6,
6,5,4,3,2,1,
三.递归遍历二叉树
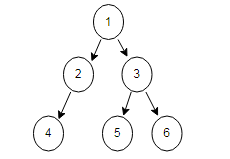
public class BTTest2 { public static void main(String[] args) { TreeNode n1 = BTUtils.generateTreeNode(new Integer[]{1,2,3,4,null,5,6}); preOrder(n1); System.out.println(); postOrder(n1); } //前序遍历 private static void preOrder(TreeNode root){ if(root==null){ return; } System.out.print(root.getVal()+","); preOrder(root.getLeft()); preOrder(root.getRight()); } //后序遍历 private static void postOrder(TreeNode root){ if(root==null){ return; } preOrder(root.getLeft()); preOrder(root.getRight()); System.out.print(root.getVal()+","); } }
输出:
1,2,4,3,5,6,
4,2,5,6,3,1,
前序遍历调用过程

后序遍历调用过程
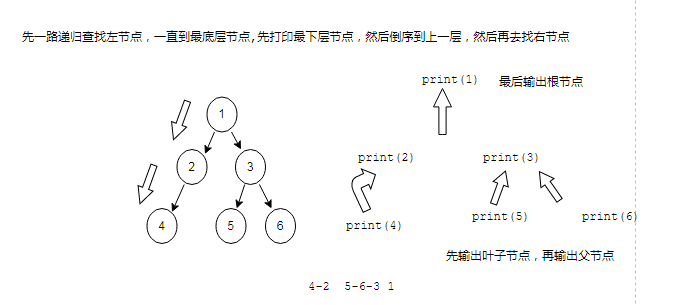
四.递归遍历多叉树,森林
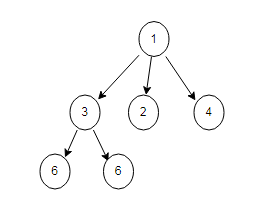
前序遍历
public class NTreeTest1{ public static void main(String[] args) { Node r1 = new Node(1); Node r21 = new Node(3); Node r22 = new Node(2); Node r23 = new Node(4); Node r31 = new Node(5); Node r32 = new Node(6); r21.children.add(r31); r21.children.add(r32); r1.children.add(r21); r1.children.add(r22); r1.children.add(r23); List<Integer> preorder = preorder(r1); ArrayUtils.displayArray(preorder); } public static List<Integer> preorder(Node root) { List<Integer> list = new ArrayList<>(); preorder(root,list); return list; } private static void preorder(Node root,List<Integer> list){ if(root==null){ return; } list.add(root.val); for (int i = 0; i < root.children.size(); i++) { preorder(root.children.get(i),list); } } }
输出: [1,3,5,6,2,4]
后序遍历
public class NTreeTest2{ public static void main(String[] args) { Node r1 = new Node(1); Node r21 = new Node(3); Node r22 = new Node(2); Node r23 = new Node(4); Node r31 = new Node(5); Node r32 = new Node(6); r21.children.add(r31); r21.children.add(r32); r1.children.add(r21); r1.children.add(r22); r1.children.add(r23); List<Integer> preorder = postorder(r1); ArrayUtils.displayArray(preorder); } public static List<Integer> postorder(Node root) { List<Integer> list = new ArrayList<>(); postorder(root,list); return list; } private static void postorder(Node root,List<Integer> list){ if(root==null){ return; } for (int i = 0; i < root.children.size(); i++) { postorder(root.children.get(i),list); } list.add(root.val); } }
输出 : [5,6,3,2,4,1]
思路和二叉树一样 ,只是把二叉树的 root.left 和root.right 改成 for循环遍历 root.children罢了.
五.递归遍历图,深度优先遍历 dfs
test1方法的图 ,和多叉树一样 邻接表
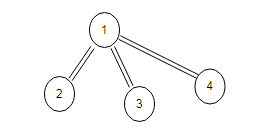
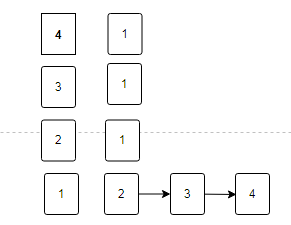
test2方法的图 邻接表
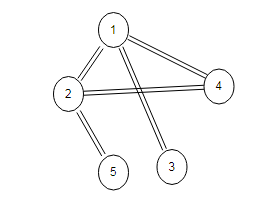
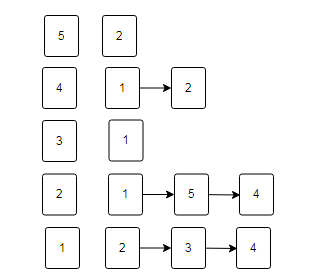
graph.java
因为图可能带环,所以用一个 Set<T> visited 来保存遍历过的图节点
public class Graph<T> {
//邻接表,这里用一个hashMap 来实现 private Map<T,LinkedList<T>> adj = new HashMap<>(); public void addEdge(T begin, T end) { if(!adj.containsKey(begin)){ adj.put(begin,new LinkedList<T>()); } if(!adj.containsKey(end)){ adj.put(end,new LinkedList<T>()); } adj.get(begin).addLast(end); adj.get(end).addLast(begin); } private void dfs(T v, Set<T> visited) {
//或者在这里加上递归退出条件,该节点遍历过就退出
//if(visited.contains(v){
//return;
//}
visited.add(v); System.out.print(v + " "); LinkedList<T> linkedList = adj.get(v);
//找邻接表的元素,从第一个元素开始找,一直找节点的邻接表的第一个,找到没有位置,或者遍历过位置 for (T t : linkedList) { if (!visited.contains(t)){ dfs(t, visited); } } } public void dfs(T v) { Set<T> visited = new HashSet<>(); dfs(v, visited); } }
GraphNode.java
public class GraphNode { private int val; public GraphNode(int val) { this.val = val; } public int getVal() { return val; } public void setVal(int val) { this.val = val; } @Override public String toString() { return "GraphNode{" + "val=" + val + '}'; } @Override public boolean equals(Object o) { if (this == o) return true; if (o == null || getClass() != o.getClass()) return false; GraphNode graphNode = (GraphNode) o; return val == graphNode.val; } @Override public int hashCode() { return Objects.hash(val); } }
Graph3Test.java
public class Graph3Test { public static void main(String[] args) { test1(); System.out.println(); test2(); } private static void test1(){ Graph<GraphNode> graph = new Graph<>(); GraphNode n1 = new GraphNode(1); GraphNode n2 = new GraphNode(2); GraphNode n3 = new GraphNode(3); GraphNode n4 = new GraphNode(4); graph.addEdge(n1,n2); graph.addEdge(n1,n3); graph.addEdge(n1,n4); graph.dfs(n1); } private static void test2(){ Graph<GraphNode> graph = new Graph<>(); GraphNode n1 = new GraphNode(1); GraphNode n2 = new GraphNode(2); GraphNode n3 = new GraphNode(3); GraphNode n4 = new GraphNode(4); GraphNode n5 = new GraphNode(5); graph.addEdge(n1,n2); graph.addEdge(n1,n3); graph.addEdge(n1,n4); graph.addEdge(n2,n5); graph.addEdge(n2,n4); graph.dfs(n1); } }
输出:
GraphNode{val=1} GraphNode{val=2} GraphNode{val=3} GraphNode{val=4}
GraphNode{val=1} GraphNode{val=2} GraphNode{val=5} GraphNode{val=4} GraphNode{val=3}
test1 的调用过程
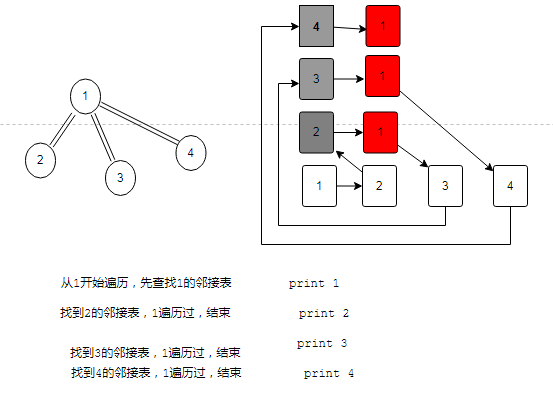
test2 的调用过程
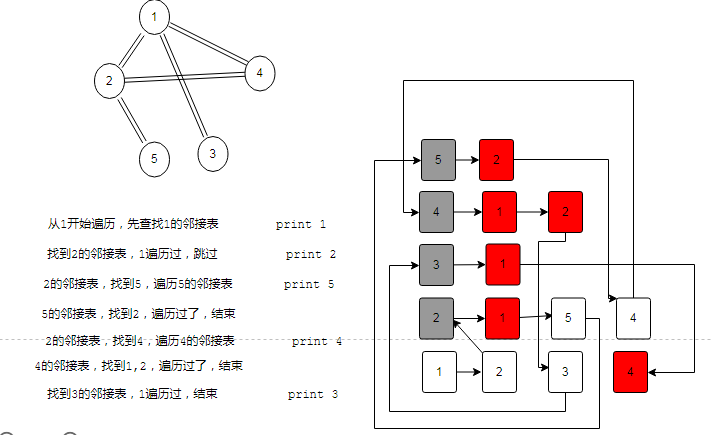
%3CmxGraphModel%3E%3Croot%3E%3CmxCell%20id%3D%220%22%2F%3E%3CmxCell%20id%3D%221%22%20parent%3D%220%22%2F%3E%3CmxCell%20id%3D%222%22%20style%3D%22edgeStyle%3Dnone%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0.867%3BentryY%3D0.086%3BentryDx%3D0%3BentryDy%3D0%3BentryPerimeter%3D0%3BstrokeColor%3D%23000000%3Bshape%3Dlink%3B%22%20edge%3D%221%22%20source%3D%225%22%20target%3D%226%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%223%22%20style%3D%22edgeStyle%3Dnone%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3Bshape%3Dlink%3B%22%20edge%3D%221%22%20source%3D%225%22%20target%3D%227%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%224%22%20style%3D%22edgeStyle%3Dnone%3Brounded%3D0%3BorthogonalLoop%3D1%3BjettySize%3Dauto%3Bhtml%3D1%3BentryX%3D0.083%3BentryY%3D0.214%3BentryDx%3D0%3BentryDy%3D0%3BentryPerimeter%3D0%3Bshape%3Dlink%3B%22%20edge%3D%221%22%20source%3D%225%22%20target%3D%228%22%20parent%3D%221%22%3E%3CmxGeometry%20relative%3D%221%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%225%22%20value%3D%221%22%20style%3D%22shape%3Dmxgraph.flowchart.on-page_reference%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22140%22%20y%3D%221998%22%20width%3D%2230%22%20height%3D%2235%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%226%22%20value%3D%222%22%20style%3D%22shape%3Dmxgraph.flowchart.on-page_reference%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%2295%22%20y%3D%222062%22%20width%3D%2230%22%20height%3D%2235%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%227%22%20value%3D%223%22%20style%3D%22shape%3Dmxgraph.flowchart.on-page_reference%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22175%22%20y%3D%222072%22%20width%3D%2230%22%20height%3D%2235%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3CmxCell%20id%3D%228%22%20value%3D%224%22%20style%3D%22shape%3Dmxgraph.flowchart.on-page_reference%3B%22%20vertex%3D%221%22%20parent%3D%221%22%3E%3CmxGeometry%20x%3D%22245.5%22%20y%3D%222054.5%22%20width%3D%2230%22%20height%3D%2235%22%20as%3D%22geometry%22%2F%3E%3C%2FmxCell%3E%3C%2Froot%3E%3C%2FmxGraphModel%3E



 浙公网安备 33010602011771号
浙公网安备 33010602011771号