5 离散概率分布的运用：善用期望

随机变量与变量

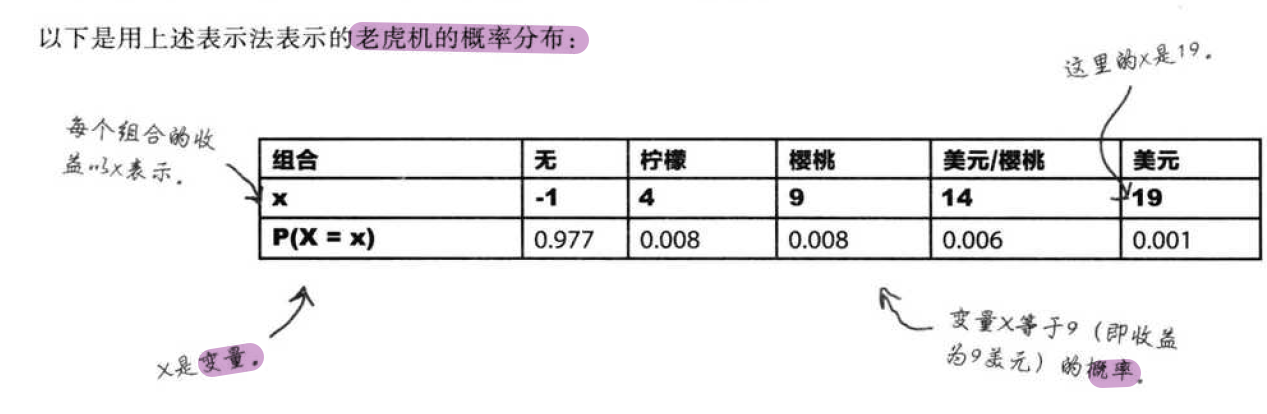
概率分布描述了一个给定变量的所有可能结果的概率;
随机变量是一个可以等于一系列数值的变量，而这一系列数值中的每一个值都与一个特定概率相关联;
在肥蛋赌场Tiger机这个例子中，随机变量代表我们将在每一局赌局中赢得的收益;
随机变量通常用大写字母表示，如X或Y;
变量能够采用的特定数值则用小写字母表示，如x或y;
于是，P(X=x)则表示“变量X取特定数值x的概率”;
这里的变量具有离散性，即该变量只能取确定数值


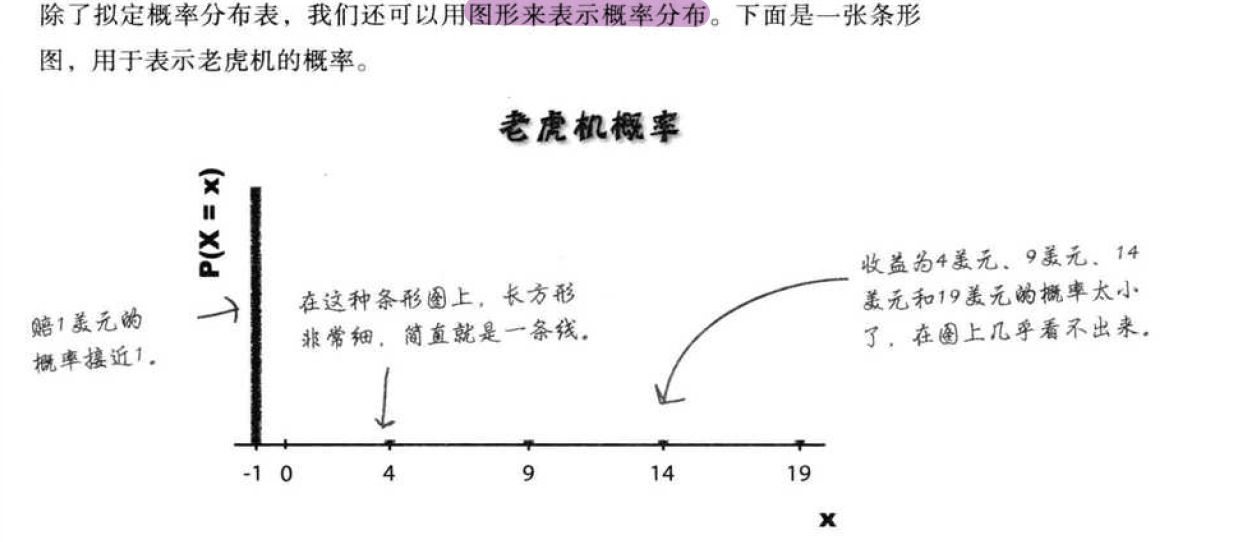
只要算出概率分布，就能利用概率分布确定预期结果。

期望

期望即所期望的长期平均结果

在多次拉杆之后，你能够期望每一局赔掉0.77美元，也就是说，如果玩100次Tiger机，你能够期望赔掉77美元

方差

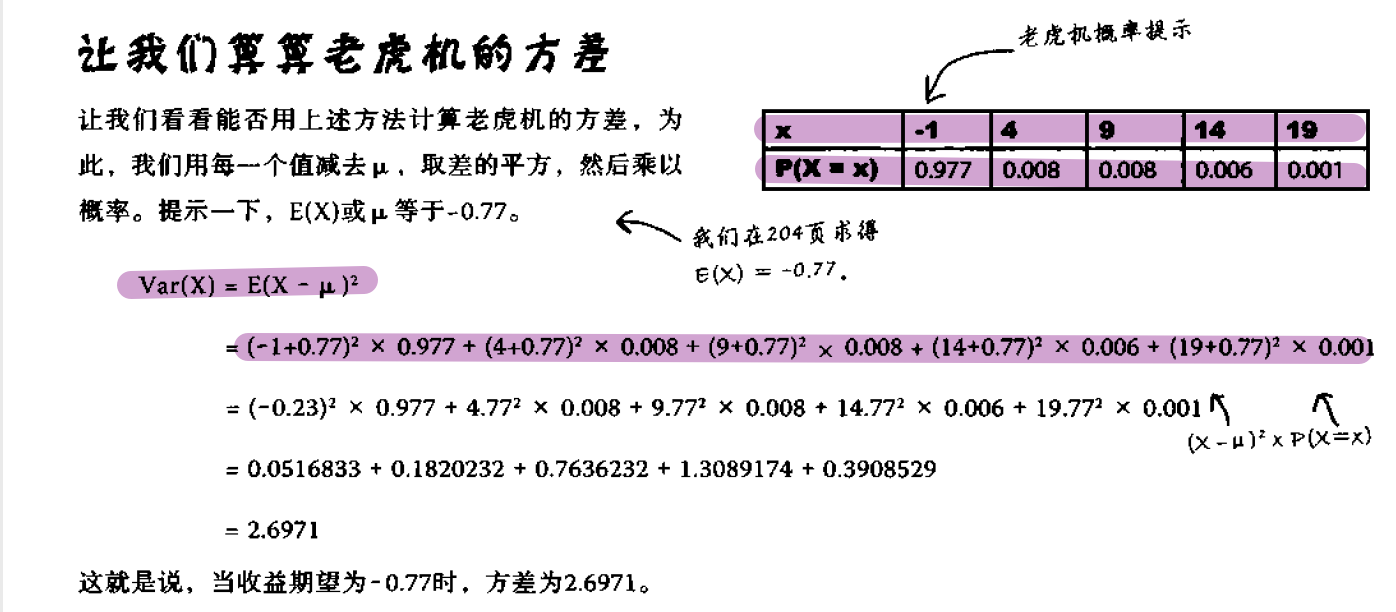
概率分布的方差和标准差是量度一些特定数值的概率的分散情况的方法

线性变换的通用公式

事件与观测值

每一局赌局称为一个事件，每一局赌局的结果称为一个观测值，每一个观测值具有相同的期望和方差

练习

相互独立的随机变量X和Y

X和Y为代表两台Tiger机的随机变量，X和Y相互独立
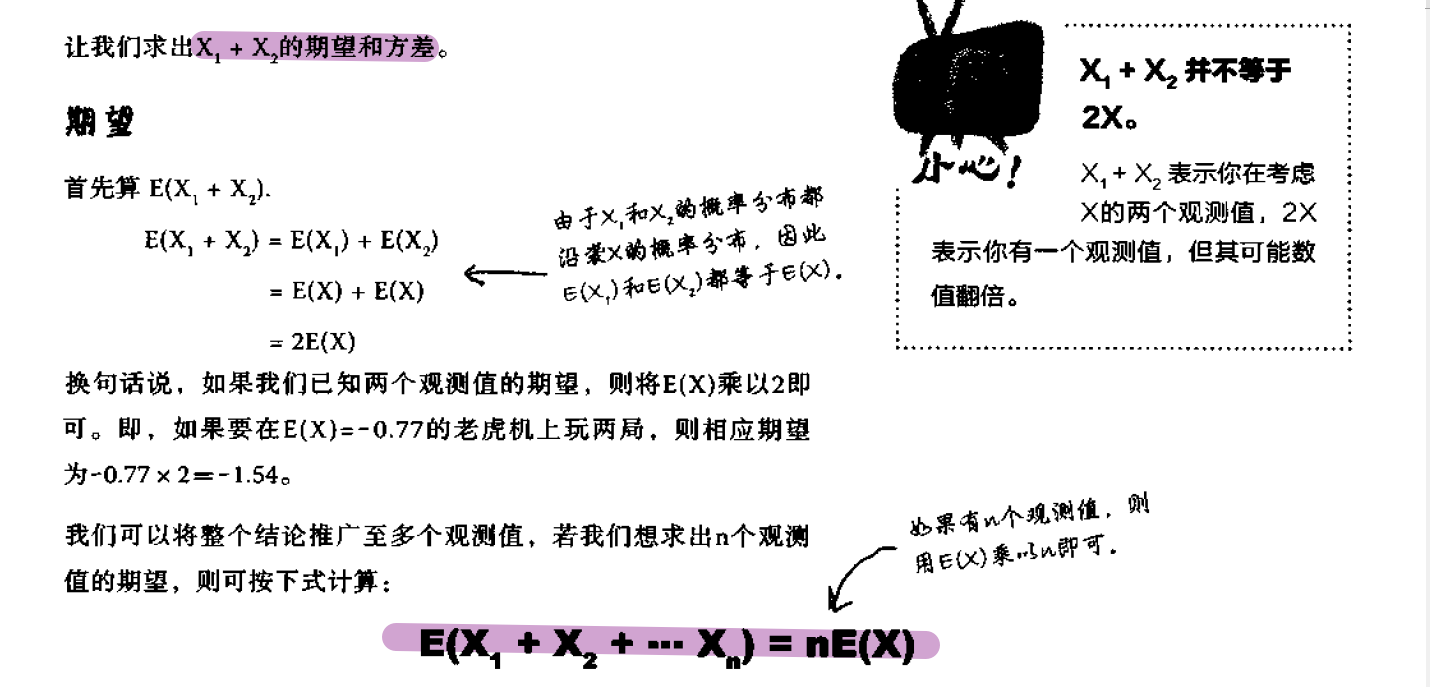
E(X+Y)=E(X)+E(Y)
Var(X+Y)=Var(X)+Var(Y)
E(X-Y)=E(X)-E(Y)
Var(X-Y)=Var(X)+Var(Y)

线性变换

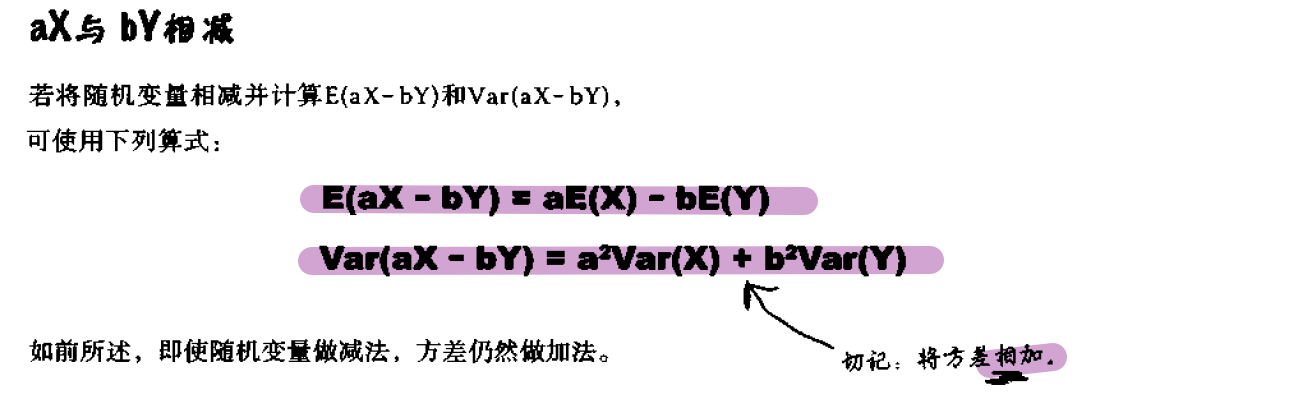
要点

练习