4 概率计算：把握机会

概率是量度某事发生几率的一种数量指标。
你可以用概率衡量发生某件事的可能性，或不会发生某事的可能性。
事件就是人们能指出其发生可能性大小的任何事情。

概率的量度尺度是0一1。
如果某件事不可能发生，则其概率为0；
如果某件事肯定会发生，则其概率为1；
大多数时候，你所面对的都是介于0和1之间的概率

维恩图：概率的图形表示，画一个方框代表样本空间S,然后画几个圆圈代表各个相关事件

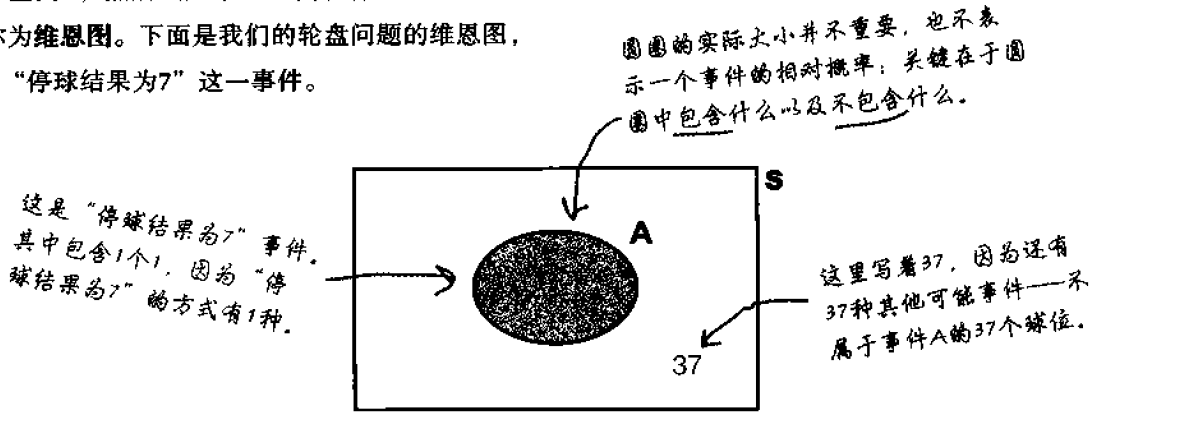
维恩图可不标出数字本身，可以选择在图上标出每一事件的实际概率，以此取代数字。
具体做法完全取决于你解决问题时需要用到的信息

A事件不发生 = A`
如果某件事属于A,就不可能属于A'；
如果某件事不属于A,就必定属于A"

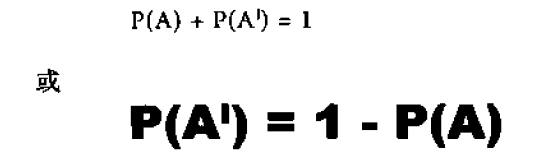
概率仅仅指出长期趋势，无论某事件多么不可能发生，只要不是完全不可能发生，该事件就仍然可能发生

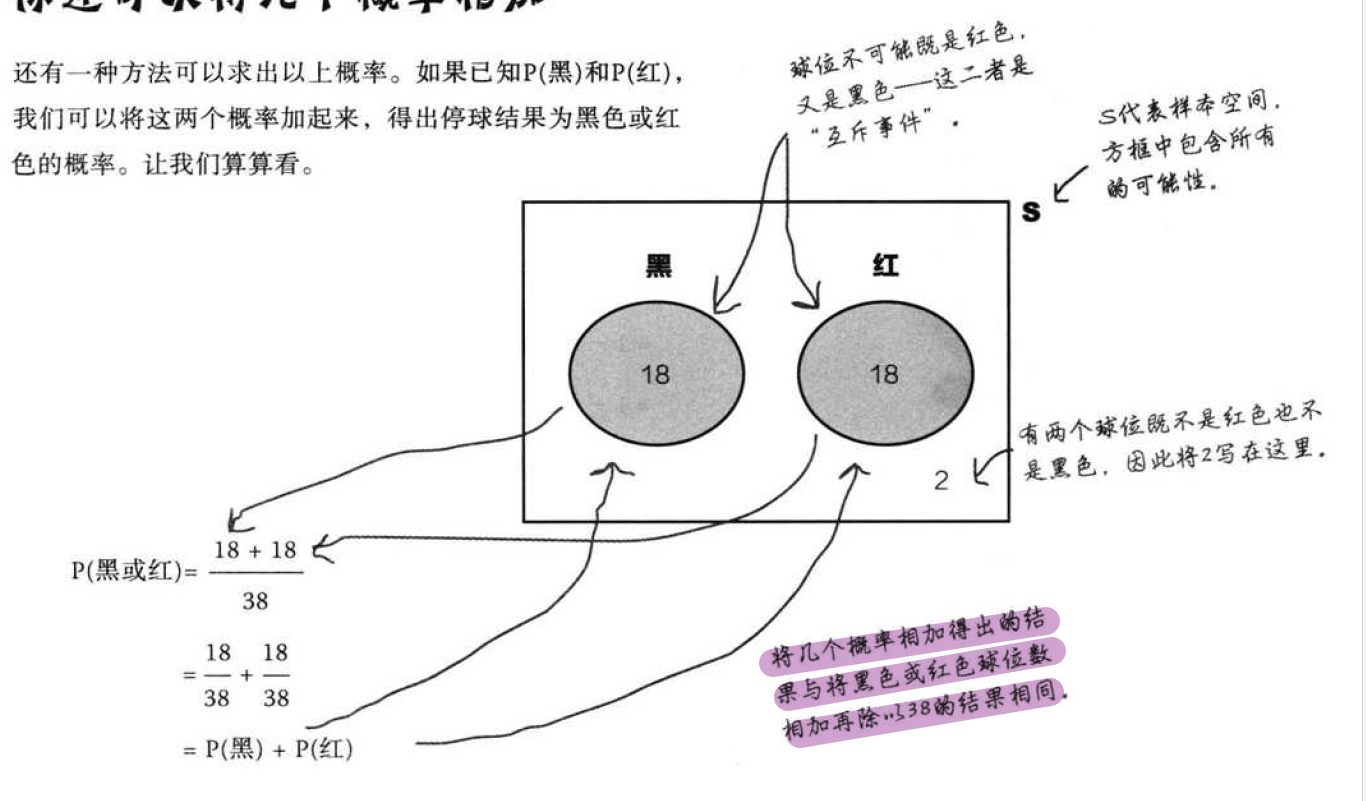
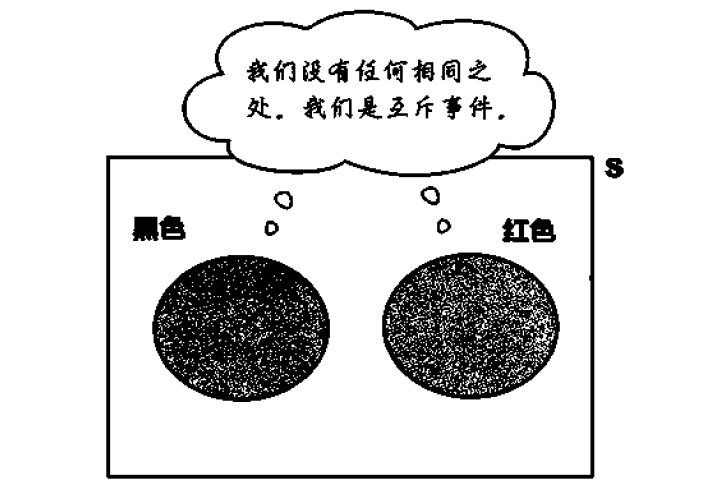
互斥事件：
如果两个事件是互斥事件，则只有其中一个事件会发生。

如果两个事件相交，则这两个事件有可能同时发生。

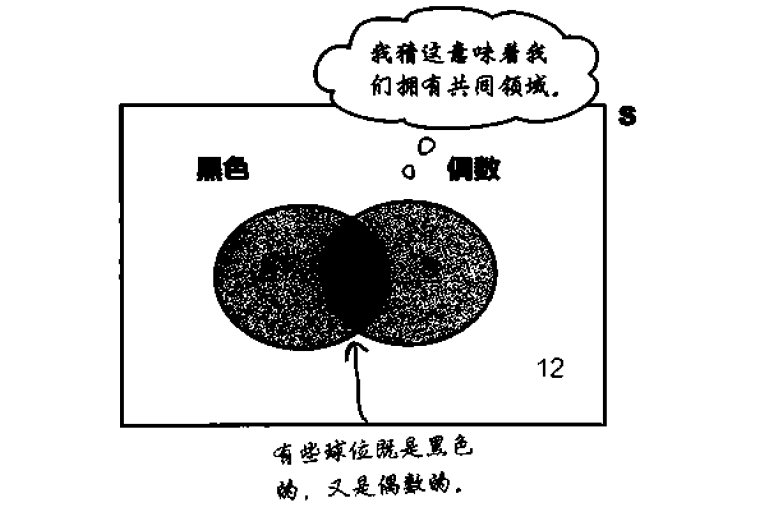
如果P(A U B)=1,则我们说A与B穷举

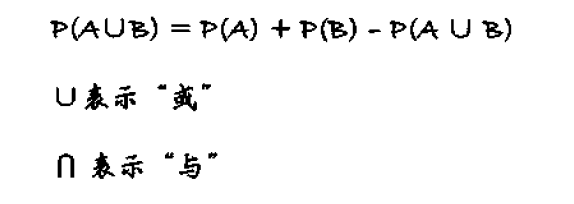
条件概率：


用概率树表示条件概率

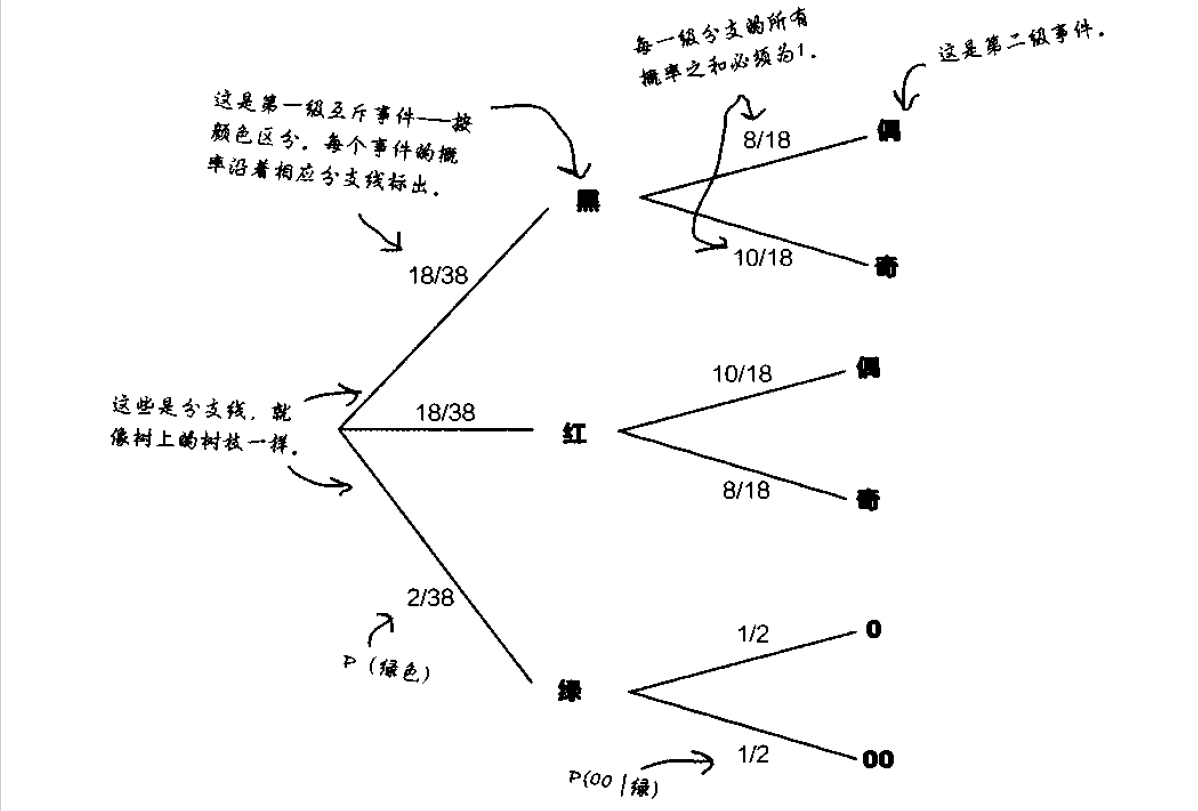
概率树不仅能帮助你以图形方式表示概率，还能帮助你计箅概率。
将一个概率乘以下一级分支概率，就可以求出包含相交情况的概率。

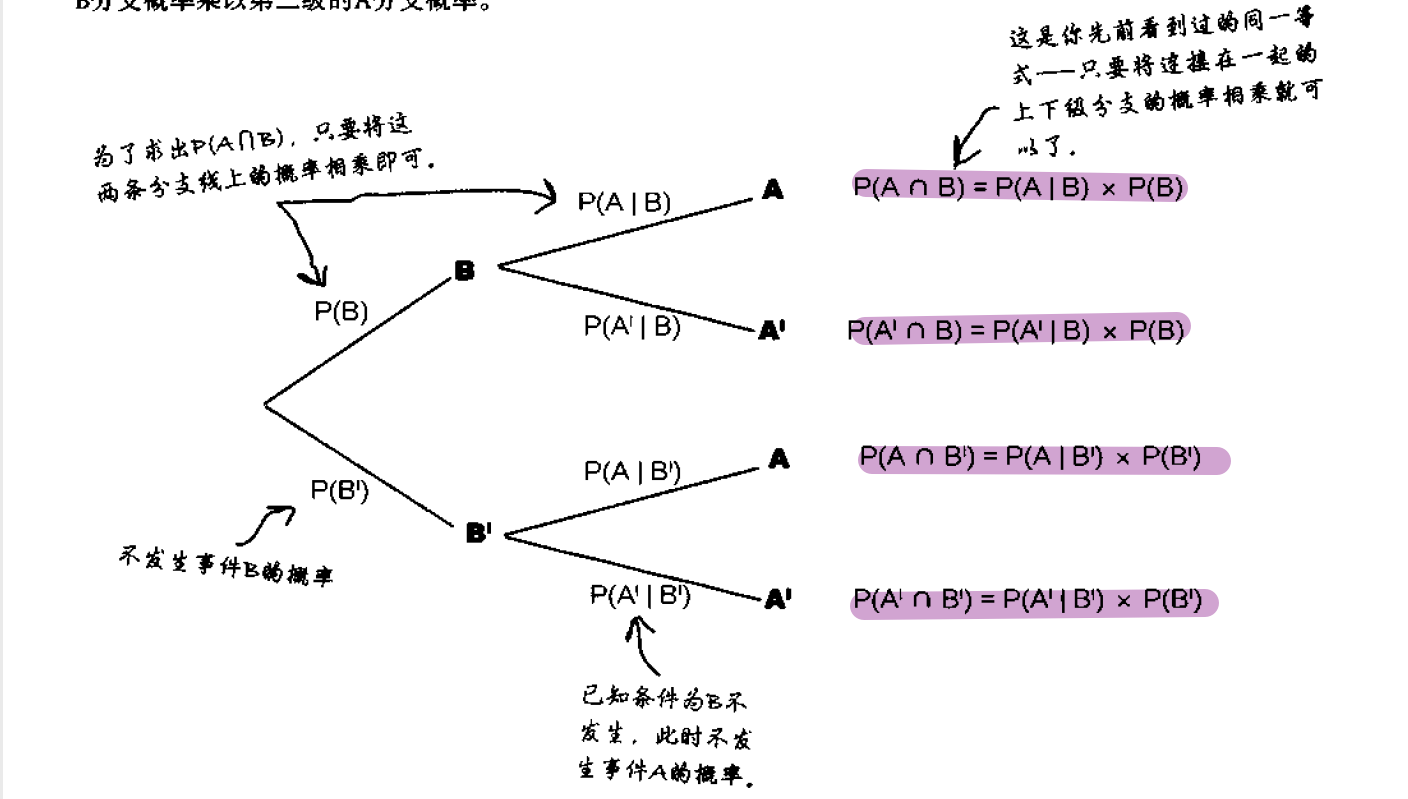
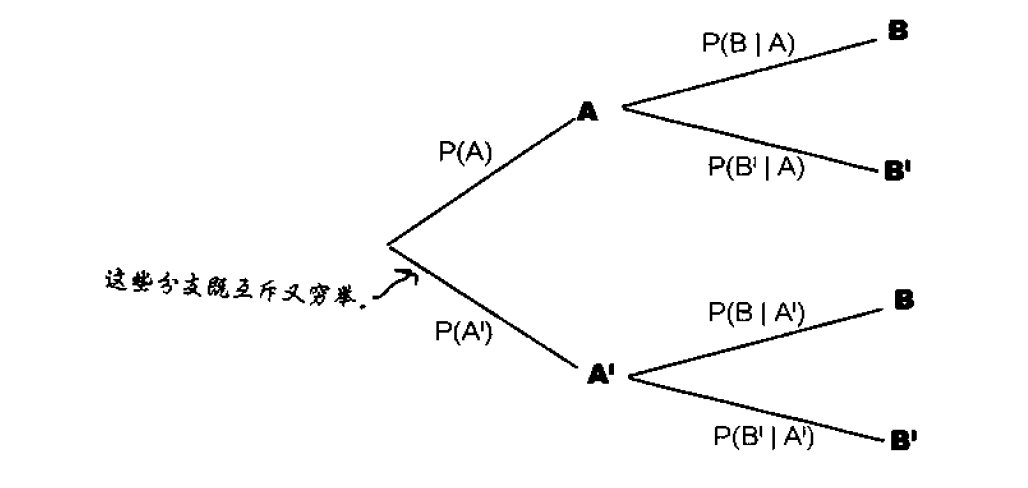
P(A∩B)=P(A)×P(B|A)

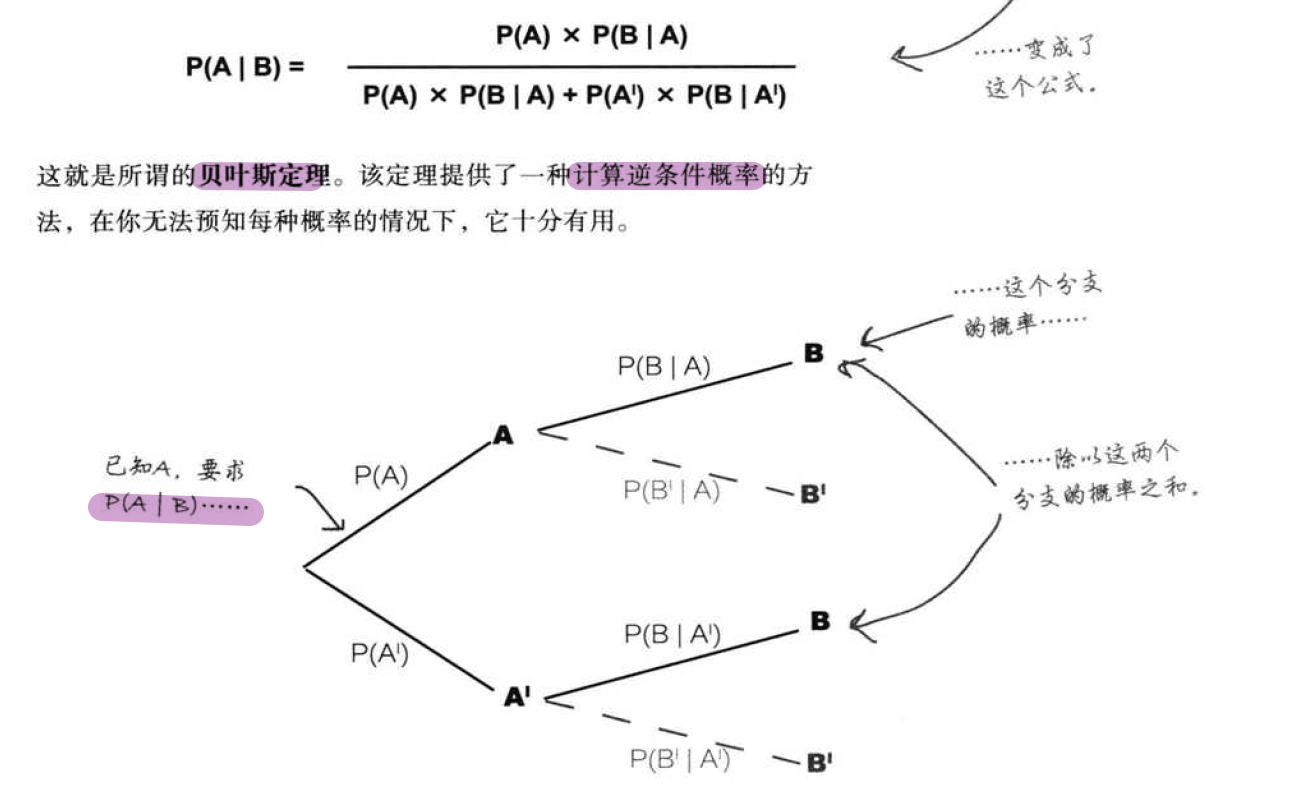
贝叶斯定理：

相关事件：
如果几个事件互有影响，则为相关事件。
如果P(A|B)与P(A)不等，则我们说事件A与事件B是相关事件一这等于说事件A与事件B的概率相互影响。
独立事件：
如果几个事件互不影响，侧为独立事件。
独立事件彼此之间互不影响。
若一个事件发生，其他事件的概率保持原样。
如果你有两个事件A和B，且P(A|B)=P(A)，则事件A和事件B必然相互独立。
如果两个事件相互独立，则通过将两个事件各自的概率相乘，可以算出同时发生这两件事的概率。
P(A ∩ B) = P(A) X P(B)
如果A、B是互斥事件，则二者不会是独立事件；如果A、B是独立事件，则二着不会是互斥事件。

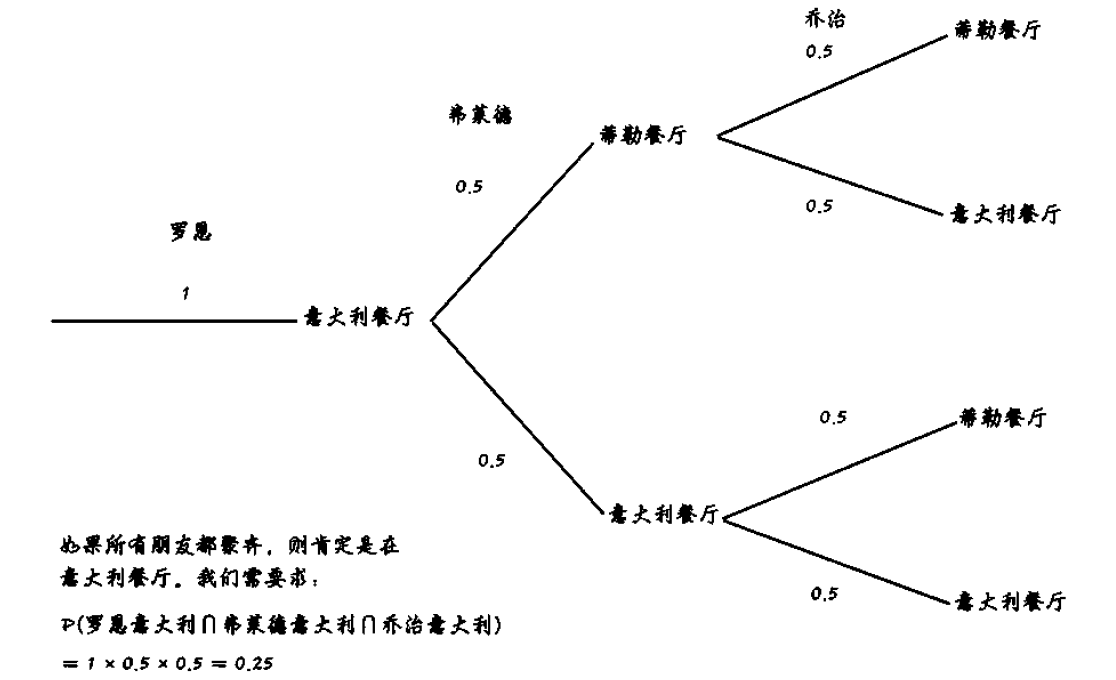
练习：