2020牛客暑期多校训练营(第二场)
A-All with Pairs
题面

样例
输入
3
ab
ba
aba
输出
29
说明
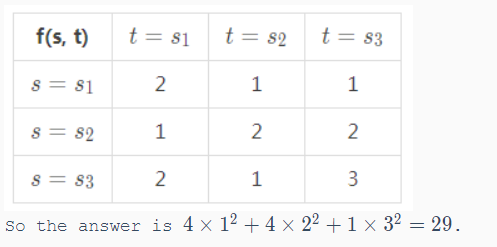
题意
给出n个字符串,求每个字符串和其他字符串(包括自己)的前缀和后缀相同的最大的长度,答案为所有长度的平方和。
题解
如果单纯求出所有的前缀和后缀相同的长度平方和,那么我们可以枚举前缀,利用hash保存所有的后缀,每次看看有多少相同的,统计答案即可。
但是由于我们要的是最大的长度,所以有一些是计算重复的,比如两个字符串“aba“,”aba”,会有两个前缀a和aba被算到,实际上a不是最长的,是不应计算的。所以我们要去重。
去重的方法就是利用kmp的nxt数组,nxt数组的含义是:nxt[i]表示最大的x,满足s[1 : x] 是s[1 : i] 的后缀,这样我们将cnt[nxt[j]]-=cnt[j]即可,因为nxt[j]代表的位置是当前枚举的前缀的后缀,所以一定被多余计算了,多余计算的值就是当前的cnt[j]。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 50;
const int M = 1e5 + 50;
const int mod = 998244353;
const int base = 233;
char s[N];
vector<long long> h[M];
vector<int> nxt[M];
ll p[N];
int cnt[N];
void getNxt(int id) {
int m = strlen(s + 1);
nxt[id].resize(m + 1);
int j = 0;
for (int i = 2; i <= m; i++) {
while (j && s[i] != s[j + 1]) j = nxt[id][j];
if (s[i] == s[j + 1]) j++;
nxt[id][i] = j;
}
}
int main() {
p[0] = 1;
for (int i = 1; i < N; i++) p[i] = p[i - 1] * base;
map<ll, int> mp;
int n; scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%s", s + 1);
int len = strlen(s + 1);
h[i].resize(len + 1);
h[i][0] = 0;
for (int j = 1; j <= len; j++) h[i][j] = h[i][j - 1] * base + s[j] - 'a' + 1;
for (int j = 0; j < len; j++) mp[h[i][len] - h[i][j] * p[len - j]]++;
getNxt(i);
}
int ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j < h[i].size(); j++) {
cnt[j] = mp[h[i][j]];
cnt[nxt[i][j]] -= cnt[j];
}
for (int j = 1; j < h[i].size(); j++)
ans = (ans + 1ll * cnt[j] * j % mod * j % mod) % mod;
}
printf("%d\n", ans);
return 0;
}
B-Boundary
题面

样例
输入
4
1 1
0 2
2 0
2 2
输出
3
题意
给出n个点,每个圆都过(0,0),找出边界上点最多的圆,输出最多的点数
题解
3点确定一个圆,枚举两个点,我们可以用两条不共线的弦中垂线的交点求出圆心,如果一个圆上含有x个点,那么有\(C(x,2)=x*(x-1)/2\)次枚举时都会求出这个圆心,所以求出最多的圆心出现次数,也就求出了答案
两条中垂线分别为
即
令
使用克莱姆法则求方程组的解即可
代码
#include <bits/stdc++.h>
#define pdd pair<double, double>
using namespace std;
typedef long long ll;
struct READ {
inline char read() {
#ifdef _WIN32
return getchar();
#endif
static const int IN_LEN = 1 << 18 | 1;
static char buf[IN_LEN], *s, *t;
return (s == t) && (t = (s = buf) + fread(buf, 1, IN_LEN, stdin)), s == t ? -1 : *s++;
}
template <typename _Tp> inline READ & operator >> (_Tp&x) {
static char c11, boo;
for(c11 = read(),boo = 0; !isdigit(c11); c11 = read()) {
if(c11 == -1) return *this;
boo |= c11 == '-';
}
for(x = 0; isdigit(c11); c11 = read()) x = x * 10 + (c11 ^ '0');
boo && (x = -x);
return *this;
}
} in;
const int N = 2e5 + 50;
const double eps = 1e-8;
int x[N], y[N];
template <typename T> T cross(T a, T b, T c, T d) {
return a * d - b * c;
}
bool check(pdd a, pdd b) {
if (fabs(a.first - b.first) > eps) return false;
if (fabs(a.second - b.second) > eps) return false;
return true;
}
int main() {
int n; in >> n;
for (int i = 1; i <= n; i++) in >> x[i] >> y[i];
int mx = 0;
vector<pdd> s;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
if (x[i] * y[j] - x[j] * y[i] == 0) continue;
ll a11 = 2 * x[i], a12 = 2 * y[i], a13 = x[i] * x[i] + y[i] * y[i];
ll a21 = 2 * x[j], a22 = 2 * y[j], a23 = x[j] * x[j] + y[j] * y[j];
ll d0 = cross(a11, a12, a21, a22);
ll d1 = cross(a13, a12, a23, a22);
ll d2 = cross(a11, a13, a21, a23);
s.push_back(pdd((double)d1 / d0, (double)d2 / d0));
}
}
sort(s.begin(), s.end());
int now = 1;
for (int i = 1; i < s.size(); i++) {
if (check(s[i], s[i - 1])) now++;
else now = 1;
mx = max(mx, now);
}
for (int i = 1; i <= 2000; i++) {
if ((i - 1) * i / 2 == mx) {
printf("%d\n", i);
break;
}
}
return 0;
}
C-Cover the Tree
题面

样例
输入
5
1 2
1 3
2 4
2 5
输出
2
2 3
4 5
说明
题意
给一棵树,求最少的链覆盖所有的边,输出最少的链的数目和方案
题解

代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct READ {
inline char read() {
#ifdef _WIN32
return getchar();
#endif
static const int IN_LEN = 1 << 18 | 1;
static char buf[IN_LEN], *s, *t;
return (s == t) && (t = (s = buf) + fread(buf, 1, IN_LEN, stdin)), s == t ? -1 : *s++;
}
template <typename _Tp> inline READ & operator >> (_Tp&x) {
static char c11, boo;
for(c11 = read(),boo = 0; !isdigit(c11); c11 = read()) {
if(c11 == -1) return *this;
boo |= c11 == '-';
}
for(x = 0; isdigit(c11); c11 = read()) x = x * 10 + (c11 ^ '0');
boo && (x = -x);
return *this;
}
} in;
const int N = 2e5 + 50;
int ind[N];
vector<int> G[N];
vector<int> s;
void dfs(int u, int f) {
if (ind[u] == 1) s.push_back(u);
for (auto v : G[u]) {
if (v != f) dfs(v, u);
}
}
int main() {
int n; in >> n;
for (int i = 1; i < n; i++) {
int u, v;
in >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
ind[u]++; ind[v]++;
}
int rt = 1;
for (int i = 1; i <= n; i++) {
if (ind[i] > 1) rt = i;
}
dfs(rt, 0);
int m = s.size();
printf("%d\n", (m + 1) / 2);
for (int i = 1; i * 2 <= m; i++) printf("%d %d\n", s[i - 1], s[i - 1 + (m + 1) / 2]);
if (m & 1) printf("%d %d\n", rt, s[(m + 1) / 2 - 1]);
return 0;
}
D-Duration
签到题
E-Exclusive Or
等待填坑,这种题不适合我
F-Fake Maxpooling
题面

样例
输入
3 4 2
输出
38
说明

题意
给出一个n*m的矩阵,矩阵中的值\(a[i][j]=lcm(i,j)\),求所有k*k子矩阵的最大值和
题解
可以使用下面的方法O(n*m)的求出矩阵的值
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (!Gcd[i][j]) {
for (int k = 1; k * i <= n && k * j <= m; k++) {
Gcd[k * i][k * j] = k;
Lcm[k * i][k * j] = i * j * k;
}
}
}
}
此题n*mlog也可以过
求出值后,使用单调队列O(n*m)的求出最大值相加即可
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct READ {
inline char read() {
#ifdef _WIN32
return getchar();
#endif
static const int IN_LEN = 1 << 18 | 1;
static char buf[IN_LEN], *s, *t;
return (s == t) && (t = (s = buf) + fread(buf, 1, IN_LEN, stdin)), s == t ? -1 : *s++;
}
template <typename _Tp> inline READ & operator >> (_Tp&x) {
static char c11, boo;
for(c11 = read(),boo = 0; !isdigit(c11); c11 = read()) {
if(c11 == -1) return *this;
boo |= c11 == '-';
}
for(x = 0; isdigit(c11); c11 = read()) x = x * 10 + (c11 ^ '0');
boo && (x = -x);
return *this;
}
} in;
const int N = 5050;
int Lcm[N][N];
int q[N];
int mn[N][N];
int main() {
int n, m, k;
in >> n >> m >> k;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (!Lcm[i][j]) {
for (int k = 1; k * i <= n && k * j <= m; k++) {
Lcm[k * i][k * j] = i * j * k;
}
}
}
}
for (int i = 1; i <= n; i++) {
int l = 1, r = 0;
for (int j = 1; j <= m; j++) {
while (l <= r && j - q[l] >= k) l++;
while (l <= r && Lcm[i][j] >= Lcm[i][q[r]]) r--;
q[++r] = j;
if (j >= k) mn[i][j] = Lcm[i][q[l]];
}
}
ll ans = 0;
for (int i = k; i <= m; i++) {
int l = 1, r = 0;
for (int j = 1; j <= n; j++) {
while (l <= r && j - q[l] >= k) l++;
while (l <= r && mn[j][i] >= mn[q[r]][i]) r--;
q[++r] = j;
if (j >= k) ans += mn[q[l]][i];
}
}
printf("%lld\n", ans);
return 0;
}
G-Greater and Greater
题面

样例
输入
6 3
1 4 2 8 5 7
2 3 3
输出
2
说明
The two subintervals are [2,8,5],[8,5,7]
题意
给出两个序列A,B,求A有多少长度为\(len(B)\)的子序列,满足子序列每一项都大于B
题解
这种数据范围可以考虑使用bitset卡常,使用bitset后,复杂度会等于\(\frac{n*m}w\)
w一般取32,跟计算机位数有关。
让每一个b[i]对应一个bitset,这个bitset的第j位为1表示a[j]>b[i],把所有bitset构造出来后,如果b[0]对应的第i位,b[1]对应的第i+1位...b[m-1]对应的第i+m-1位均为1,则说明a数组从i开始的一段长为m的子区间是满足答案的,也就对答案贡献1。
为了方便统计,可以让b[i]对应的bitset右移i位(i从0开始),这样如果有一列的与为1,则说明从这一列开始的m长度区间是满足答案的。
还可以发现,如果把a,b分别排序,同时记录原位置,开一个pair记录,first为值,second为位置。那么这m个bitset是存在递推关系的,从b最大的开始,较小的数可以直接继承较大数的bitset,然后将\(a[j].first>b[i].first\)的\(a[j].second\)位置1,就得到了\(b[i].second\)对应的bitset,然后把这m个bitset做&操作,统计最后1的个数即为答案。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct READ {
inline char read() {
#ifdef _WIN32
return getchar();
#endif
static const int IN_LEN = 1 << 18 | 1;
static char buf[IN_LEN], *s, *t;
return (s == t) && (t = (s = buf) + fread(buf, 1, IN_LEN, stdin)), s == t ? -1 : *s++;
}
template <typename _Tp> inline READ & operator >> (_Tp&x) {
static char c11, boo;
for(c11 = read(),boo = 0; !isdigit(c11); c11 = read()) {
if(c11 == -1) return *this;
boo |= c11 == '-';
}
for(x = 0; isdigit(c11); c11 = read()) x = x * 10 + (c11 ^ '0');
boo && (x = -x);
return *this;
}
} in;
const int N = 2e5 + 50;
bitset<N> ans, bs;
pair<int, int> a[N], b[N];
int main() {
int n, m; in >> n >> m;
for (int i = 0; i < n; i++) {
in >> a[i].first;
a[i].second = i;
}
for (int i = 0; i < m; i++) {
in >> b[i].first;
b[i].second = i;
}
sort(a, a + n);
sort(b, b + m);
ans.set();
for (int i = m - 1, j = n - 1; i >= 0; i--) {
while (j >= 0 && a[j].first >= b[i].first) {
bs.set(a[j].second);
j--;
}
ans &= bs >> b[i].second;
}
printf("%d\n", ans.count());
return 0;
}
H-Happy Triangle
题面

样例
输入
8
1 1
3 1
1 1
3 2
3 1
1 2
2 1
3 1
输出
No
No
Yes
No
题意
q次操作,操作1代表向multiset中插入一个x,操作2代表从multiset中删除x,操作3询问multiset中是否存在两个数与x可以构成三角形,对于每个操作3,输出yes/no
题解
首先,在回答询问的时候可以只考虑相邻的两个数。因为对于一组a,b,x,不妨设\(a \le b\),如果能构成三角形,a可以换成b的前驱而不影响答案。
对于3操作,分类讨论
-
x是最大边,那么找到x的两个前驱a,b,判断\(a+b>x\)是否成立即可
-
x不是最大边,那么需要找到相邻的两个数a,b,\(b \ge x, a+x \ge b\)即\(x \ge b - a\),所以对于每个数维护它和它前驱的差,查询时找到大于x的差的最小值与x比较。
对于第一种情况,维护一个multiset即可,对于第二种情况,可以使用动态开点线段树,每个点的下标是它的值,权值为它与他前驱的差,使用一个map来判断增加的值是否重复,删除是否把一个值删除完。
代码
#include <bits/stdc++.h>
#define mid (l+r>>1)
using namespace std;
typedef long long ll;
struct READ {
inline char read() {
#ifdef _WIN32
return getchar();
#endif
static const int IN_LEN = 1 << 18 | 1;
static char buf[IN_LEN], *s, *t;
return (s == t) && (t = (s = buf) + fread(buf, 1, IN_LEN, stdin)), s == t ? -1 : *s++;
}
template <typename _Tp> inline READ & operator >> (_Tp&x) {
static char c11, boo;
for(c11 = read(),boo = 0; !isdigit(c11); c11 = read()) {
if(c11 == -1) return *this;
boo |= c11 == '-';
}
for(x = 0; isdigit(c11); c11 = read()) x = x * 10 + (c11 ^ '0');
boo && (x = -x);
return *this;
}
} in;
const int N = 2e6 + 50;
const int inf = 0x3f3f3f3f;
multiset<int> st;
map<int, int> mp;
int mn[N << 2], L[N << 2], R[N << 2], tot, rt;
void pushup(int o) {
mn[o] = min(mn[L[o]], mn[R[o]]);
}
void update(int &o, int l, int r, int x, int v) {
if (!o) o = ++tot;
if (l == r) {
mn[o] = v;
return;
}
if (x <= mid) update(L[o], l, mid, x, v);
else update(R[o], mid + 1, r, x, v);
pushup(o);
}
int query(int o, int l, int r, int ql, int qr) {
if (!o) return inf;
if (l == ql && r == qr) return mn[o];
if (qr <= mid) return query(L[o], l, mid, ql, qr);
else if (ql > mid) return query(R[o], mid + 1, r, ql, qr);
else return min(query(L[o], l, mid, ql, mid), query(R[o], mid + 1, r, mid + 1, qr));
}
void ins(int x) {
mp[x]++;
if (!st.size()) {
st.insert(x);
return;
}
if (mp[x] == 1) {
auto it = mp.lower_bound(x);
++it;
if (it != mp.end() && it->second == 1) update(rt, 1, 1e9, it->first, it->first - x);
--it;
int y = -1e9;
if (it != mp.begin()) y = prev(it)->first;
update(rt, 1, 1e9, x, x - y);
}
else if (mp[x] == 2) update(rt, 1, 1e9, x, 0);
st.insert(x);
}
void del(int x) {
auto it = mp.lower_bound(x);
mp[x]--;
int y = -1e9;
if (it != mp.begin()) y = prev(it)->first;
if (mp[x] == 0) {
if ((++it) != mp.end() && it->second == 1) {
update(rt, 1, 1e9, it->first, it->first - y);
}
update(rt, 1, 1e9, x, inf);
mp.erase(x);
}
else if (mp[x] == 1) update(rt, 1, 1e9, x, x - y);
st.erase(st.lower_bound(x));
}
void calc(int x) {
bool ok = false;
if (st.size() < 2) {
puts("No");
return;
}
auto it = st.upper_bound(x);
int a = -inf, b = -inf;
if (it != st.begin()) a = *(--it);
if (it != st.begin()) b = *(--it);
if (a + b > x) ok = true;
if (query(rt, 1, 1e9, x, 1e9) < x) ok = true;
if (ok) puts("Yes");
else puts("No");
}
int main() {
int q; in >> q;
memset(mn, inf, sizeof(mn));
while (q--) {
int op, x; in >> op >> x;
if (op == 1) ins(x);
else if (op == 2) del(x);
else calc(x);
}
return 0;
}
I-Interval
待填坑
J-Just Shuffle
题面

样例
输入
3 998244353
2 3 1
输出
3 1 2
题意
给出一个长度为n的排列\(A\)和k,求一个置换,将$ {1,2,\dots n} \(做k次这个置换后可以得到排列A,求将\) {1,2,\dots n} $做1次这个置换后的值
题解
首先把A所有环求出来,设环长为\(l\),由于k是大质数,所以可以求出k在模\(l\)意义下的逆元\(inv_i\),这样把这个环逆向转\(inv_i\)次就可以得到旋转1次的环,也就是所要求的答案。
逆元可以用欧拉定理求

代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct READ {
inline char read() {
#ifdef _WIN32
return getchar();
#endif
static const int IN_LEN = 1 << 18 | 1;
static char buf[IN_LEN], *s, *t;
return (s == t) && (t = (s = buf) + fread(buf, 1, IN_LEN, stdin)), s == t ? -1 : *s++;
}
template <typename _Tp> inline READ & operator >> (_Tp&x) {
static char c11, boo;
for(c11 = read(),boo = 0; !isdigit(c11); c11 = read()) {
if(c11 == -1) return *this;
boo |= c11 == '-';
}
for(x = 0; isdigit(c11); c11 = read()) x = x * 10 + (c11 ^ '0');
boo && (x = -x);
return *this;
}
} in;
const int N = 2e5 + 50;
int a[N];
int f[N], p[N];
int tot;
void euler(int n) {
f[1] = 1;
for (int i = 2; i <= n; i++) {
if (!f[i]) p[++tot] = i, f[i] = i - 1;
for (int j = 1; j <= tot && i * p[j] <= n; j++) {
if (i % p[j] == 0) {
f[i * p[j]] = f[i] * p[j];
break;
}
f[i * p[j]] = f[i] * (p[j] - 1);
}
}
}
int vis[N];
int qpow(int a, int b, int p) {
int ans = 1;
while (b) {
if (b & 1) ans = 1ll * ans * a % p;
a = 1ll * a * a % p;
b >>= 1;
}
return ans;
}
int ans[N];
int main() {
int n, k; in >> n >> k;
euler(n);
for (int i = 1; i <= n; i++) in >> a[i];
for (int i = 1; i <= n; i++) {
if (vis[i]) continue;
vis[i] = 1;
int j = i;
vector<int> b;
b.push_back(j);
while (a[j] != i) {
b.push_back(a[j]);
j = a[j];
vis[j] = 1;
}
int r = qpow(k % b.size(), f[b.size()] - 1, b.size());
for (int i = 0; i < b.size(); i++) {
ans[b[i]] = b[(i + r) % b.size()];
}
}
for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
return 0;
}
K-Keyboard Free
待填坑


