UVA-12633 Super Rooks on Chessboard

Description

Let’s assume there is a new chess piece named Super-rook. When placed at a cell of a chessboard, it attacks all the cells that belong to the same row or same column. Additionally it attacks all the cells of the diagonal that goes from top-left to bottom-right direction through that cell.

N Super-rooks are placed on a R × C chessboard. The rows are numbered 1 to R from top to

bottom and columns are numbered 1 to C from left to right of the chessboard. You have to find the number of cells of the chessboard which are not attacked by any of the Super-rooks.

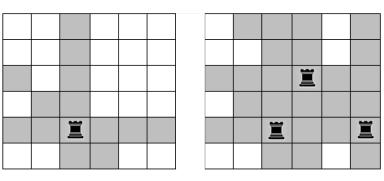
The picture on the left shows the attacked cells when a Super-rook is placed at cell (5, 3) of a 6 × 6 chessboard. And the picture on the right shows the attacked cells when three Super-rooks are placed at cells (3, 4), (5, 3) and (5, 6). These pictures (Left and right one) corresponds to the first and second sample input respectively

Input

First line of input contains an integer T (1 ≤ T ≤ 20) which is the number of test cases. The first
line of each test case contains three integers R, C and N (1 ≤ R; C; N ≤ 50; 000). The next N lines
contain two integers r, c giving the row and column of a Super-rook on the chessboard (1 ≤ r ≤ R and 1 ≤ c ≤ C). You may assume that two Super-rooks won’t be placed on the same cell.

Output

For each test case, output the case number followed by the number of cells which are not attacked by any of the Super-rook.

Sample Input

2
6 6 1
5 3
6 6 3
3 4
5 3
5 6

Sample Output

Case 1: 22
Case 2: 9  

题意

在\(r\times c\)的棋盘上放置一些超级车,可以攻击同一行同一列和同一主对角线,问有多少个格子不被攻击

题解

如果放置的是普通车,那么答案很简单,就是没被占的行数乘以没被占的列数

现在我们要考虑主对角线的影响,我们把没被占的行数和没被占的列数和被占用的对角线处理出来,由于x-y+c唯一确定了一条对角线的编号,所以我们就可以用fft算出一条被占用对角线上到底有多少格子是之前没被占用的.

方法就是我们让被占的行对应的系数为0,没被占的行系数为1,列也同样如此,这样卷积之后,\(a[i]\)的系数即代表编号为\(i\)的对角线上没被占用的格子数,我们先把不考虑对角线影响的答案\(numx*numy\)算出,遍历每一条对角线,如果它被占了,就减去被占的对角线上之前没有考虑的格子数,即可得到答案

代码

#include <bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
typedef long long ll;

struct cp {
    double r, i;
    cp(double r = 0, double i = 0): r(r), i(i) {}
    cp operator + (const cp &b) {
        return cp(r + b.r, i + b.i);
    }
    cp operator - (const cp &b) {
        return cp(r - b.r, i - b.i);
    }
    cp operator * (const cp &b) {
        return cp(r * b.r - i * b.i, r * b.i + i * b.r);
    }
};
void change(cp a[], int len) {
    for (int i = 1, j = len / 2; i < len - 1; i++) {
        if (i < j) swap(a[i], a[j]);
        int k = len / 2;
        while (j >= k) {
            j -= k;
            k /= 2;
        }
        if (j < k) j += k;
    }
}
void fft(cp a[], int len, int op) {
    change(a, len);
    for (int h = 2; h <= len; h <<= 1) {
        cp wn(cos(-op * 2 * pi / h), sin(-op * 2 * pi / h));
        for (int j = 0; j < len; j += h) {
            cp w(1, 0);
            for (int k = j; k < j + h / 2; k++) {
                cp u = a[k];
                cp t = w * a[k + h / 2];
                a[k] = u + t;
                a[k + h / 2] = u - t;
                w = w * wn;
            }
        }
    }
    if (op == -1) {
        for (int i = 0; i < len; i++) {
            a[i].r /= len;
        }
    }
}

const int N = 4e5 + 50;

int visx[N], visy[N], visxy[N];
cp a[N], b[N];


int main() {
    int t;
    int cse = 0;
    scanf("%d", &t);
    while (t--) {
        int r, c, n;
        scanf("%d%d%d", &r, &c, &n);
        int len1 = r + c + 1;
        int len = 1;
        while (len < len1) len <<= 1;
        for (int i = 0; i < len; i++) {
            a[i] = cp(0, 0);
            b[i] = cp(0, 0);
            visx[i] = visy[i] = visxy[i] = 0;
        }
        for (int i = 0; i < n; i++) {
            int x, y;
            scanf("%d%d", &x, &y);
            x--, y--;
            visx[x] = 1;
            visy[y] = 1;
            visxy[x - y + c - 1] = 1;
        }
        ll numx = 0, numy = 0;
        for (int i = 0; i < r; i++) {
            if (visx[i] == 0) {
                numx++;
                a[i] = cp(1, 0);
            }
        }
        for (int i = 0; i < c; i++) {
            if (visy[i] == 0) {
                numy++;
                b[c - i - 1] = cp(1, 0);
            }
        }
        fft(a, len, 1);
        fft(b, len, 1);
        for (int i = 0; i < len; i++) {
            a[i] = a[i] * b[i];
        }
        fft(a, len, -1);
        ll res = numx * numy;
        for (int i = 0; i < len; i++) {
            res -= (ll)(a[i].r + 0.5) * visxy[i];
        }
        printf("Case %d: %lld\n", ++cse, res);
    }
    return 0;
}