树链剖分入门

简介

树链剖分就是将树划分为多条链，将每条链映射到序列上，然后使用线段树，平衡树等数据结构来维护每条链的信息。

树剖将树链映射到序列上后用线段树等数据结构来维护树链信息，所以可以像区间修改，区间查询一样进行树上路径的修改、查询等操作

基本概念

重儿子：子树结点数目最多的儿子（size最大的点）；

重边：父亲结点和重儿子连成的边；

重链：由多条重边连接而成的路径；

轻儿子: 除了重儿子，其余都为轻儿子；

轻边：重边之外的边；

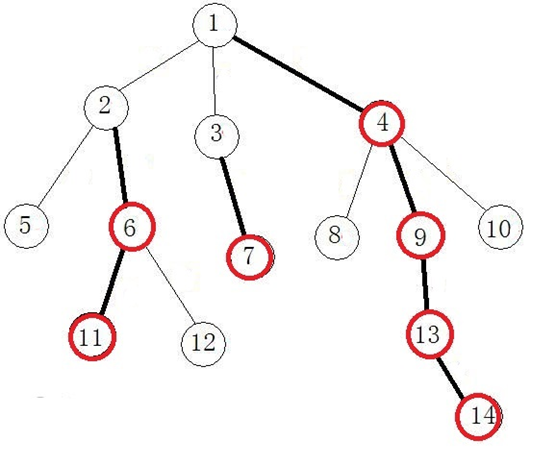
红圈表示重儿子;

黑边表示重边;

由黑边连成的链即为重链

实现

第一遍dfs处理出重儿子，深度，父亲等信息

第二遍dfs处理出结点所在重链的链顶，dfs序

上图中的树处理完毕后dfs序如下

可以发现，由于我们优先dfs重儿子，所以重儿子结点的编号是连续的，于是一条重链就被映射成了一段连续的区间；

这样树上两点间的路径就被分割成了多个连续的区间，如

（12，8) 可分割成 12，2 - 6, 1 – 4, 8 四段

（11，13）可分成 2-6-11，1 – 4 -9 -13 两段

于是我们就可以使用线段树来进行树链修改与查询了

时间复杂度

每次都将路径分割成多个区间，区间操作可以在O(logn)内解决， 但如果分割成的区间数很多怎么办？！

那我们就来看下两点间的路径最多会分割成多少段。

这时候重儿子就发挥作用了，由于每条链的链顶都是一个轻儿子，轻儿子的大小肯定小于重儿子, 所以size[轻儿子]<=size[父亲]/2

这样从上往下每进入一条新链，结点的个数就会除2，所以经过的链数就是log级别的了。

树剖每次将路径分成log个区间，然后区间操作一般都会用到线段树之类的数据结构来维护，所以一般情况下一次操作的时间复杂度为(logn)^2

例题

树的统计

Description

一棵树上有n个节点，编号分别为1到n，每个节点都有一个权值w。我们将以下面的形式来要求你对这棵树完成一些操作：

I. CHANGE u t : 把结点u的权值改为t

II. QMAX u v: 询问从点u到点v的路径上的节点的最大权值 I

II. QSUM u v: 询问从点u到点v的路径上的节点的权值和

注意：从点u到点v的路径上的节点包括u和v本身

Input

输入的第一行为一个整数n，表示节点的个数。接下来n – 1行，每行2个整数a和b，表示节点a和节点b之间有一条边相连。接下来n行，每行一个整数，第i行的整数wi表示节点i的权值。接下来1行，为一个整数q，表示操作的总数。接下来q行，每行一个操作，以“CHANGE u t”或者“QMAX u v”或者“QSUM u v”的形式给出。

对于100％的数据，保证1<=n<=30000，0<=q<=200000；中途操作中保证每个节点的权值w在-30000到30000之间。

Output

对于每个“QMAX”或者“QSUM”的操作，每行输出一个整数表示要求输出的结果。

Sample Input

4
1 2
2 3
4 1
4 2 1 3
12
QMAX 3 4
QMAX 3 3
QMAX 3 2
QMAX 2 3
QSUM 3 4
QSUM 2 1
CHANGE 1 5
QMAX 3 4
CHANGE 3 6
QMAX 3 4
QMAX 2 4
QSUM 3 4

Sample Output

4
1
2
2
10
6
5
6
5
16

题解

树剖模板题,树链剖分后用线段树维护即可

#include <bits/stdc++.h>
#define lson (o << 1)
#define rson (o << 1 | 1)
using namespace std;
const int N = 3e4 + 10;
typedef long long ll;
vector<int> G[N];
const ll inf = 1e9;
int n;
int val[N];
int fa[N];
int son[N];
int sze[N];
int dep[N];
void dfs1(int u, int f) {
    sze[u] = 1;
    fa[u] = f;
    son[u] = 0;
    dep[u] = dep[f] + 1;
    for (int i = 0; i < G[u].size(); i++) {
        int v = G[u][i];
        if (v == f) continue;
        dfs1(v, u);
        sze[u] += sze[v];
        if (sze[v] > sze[son[u]]) son[u] = v;
    }
}
int top[N];
int cnt;
int pos[N];
int a[N];
void dfs2(int u, int f, int t) {
    top[u] = t;
    pos[u] = ++cnt;
    a[cnt] = val[u];
    if (son[u]) dfs2(son[u], u, t);
    for (int i = 0; i < G[u].size(); i++) {
        int v = G[u][i];
        if (v == f || v == son[u]) continue;
        dfs2(v, u, v);
    }
}
ll sumv[N << 2];
ll maxv[N << 2];
void pushup(int o) {
    sumv[o] = sumv[lson] + sumv[rson];
    maxv[o] = max(maxv[lson], maxv[rson]);
}
void build(int o, int l, int r) {
    if (l == r) {
        sumv[o] = a[l];
        maxv[o] = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(lson, l, mid); build(rson, mid + 1, r);
    pushup(o);
}
void update(int o, int l, int r, int pos, ll v) {
    if (l == r) {
        sumv[o] = v;
        maxv[o] = v;
        return;
    }
    int mid = (l + r) >> 1;
    if (pos <= mid) update(lson, l, mid, pos, v);
    else update(rson, mid + 1, r, pos, v);
    pushup(o);
}
ll querysum(int o, int l, int r, int ql, int qr) {
    if (ql <= l && r <= qr) {
        return sumv[o];
    }
    ll ans = 0; int mid = (l + r) >> 1;
    if (ql <= mid) ans += querysum(lson, l, mid, ql, qr);
    if (qr > mid) ans += querysum(rson, mid + 1, r, ql, qr);
    return ans;
}
ll querymax(int o, int l, int r, int ql, int qr) {
    if (ql <= l && r <= qr) {
        return maxv[o];
    }
    ll ans = -inf; int mid = (l + r) >> 1;
    if (ql <= mid) ans = max(ans, querymax(lson, l, mid, ql, qr));
    if (qr > mid) ans = max(ans, querymax(rson, mid + 1, r, ql, qr));
    return ans;
}
ll calcsum(int u, int v) {
    ll ans = 0;
    while (top[u] != top[v]) {//当不在同一条链上
        if (dep[top[u]] < dep[top[v]]) swap(u, v);//每次深度较大的点向上走
        ans += querysum(1, 1, n, pos[top[u]], pos[u]);
        u = fa[top[u]];//进入新的链
    }
    if (dep[u] < dep[v]) swap(u, v);//进入同一条链再求一次
    ans += querysum(1, 1, n, pos[v], pos[u]);
    return ans;
}
ll calcmax(int u, int v) {
    ll ans = -inf;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        ans = max(ans, querymax(1, 1, n, pos[top[u]], pos[u]));
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) swap(u, v);
    ans = max(ans, querymax(1, 1, n, pos[v], pos[u]));
    return ans;
}
int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    scanf("%d", &n);
    for (int i = 1; i < n; i++) {
        int u, v;
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    for (int i = 1; i <= n; i++) scanf("%d", &val[i]);
    dep[0] = 0;
    dfs1(1, 0);
    cnt = 0;
    dfs2(1, 0, 1);
    build(1, 1, n);
    int m;
    scanf("%d", &m);
    char ch[10];
    for (int i = 1; i <= m; i++) {
        scanf("%s", ch);
        int l, r, k;
        ll v;
        switch(ch[1]) {
            case 'M': scanf("%d%d", &l, &r); printf("%lld\n", calcmax(l, r)); break;
            case 'S': scanf("%d%d", &l, &r); printf("%lld\n", calcsum(l, r)); break;
            case 'H': scanf("%d%lld", &k, &v); update(1, 1, n, pos[k], v); break;
        }
    }
    return 0;
}