平衡树(Splay) artalter级服务:第一弹——旋转的艺术
平衡树(Splay) artalter 级服务:第一弹——旋转的艺术
0.前言
本蒟蒻前不久刚学SPLAY,有了一点心得,想要巩固下来。同时也觉得网上的神犇们实在太强了,有的内容并不能很好的让我这样的蒟蒻理解,因此便有了我这篇RBQ级服务的博客。我的splay是看自有风月马前卒学的,因此部分代码可能有些相似。自有风月马前卒是一位高产的神犇,强烈推荐大家看他的博客
1.引入:何为平衡树
平衡树,大家一定都听说过(毕竟没听说过也不会来找Splay博客),那么,平衡树到底是怎么回事呢?就让小编一起带大家来看看吧
平衡树是一种 二叉搜索树(BST) ,它拥有二叉搜索树的重要性质:对于BST的一个节点,它的左子树都比它小,右子树都比它大。BST因为有了这个性质,就可以以\(O(mh)\)的复杂度方便的实现插入,删除,查询前后驱,排名,k小值等功能。没错,正是平衡树常用的功能。好的,BST取代了平衡树,本篇完————
怎么可能???
BST的性质可以理解为,它是一个中序遍历为有序数列的二叉树,而我们知道,对于一棵树,只知道中序遍历是无法确定它的形态的,因此,插入顺序的不同会导致BST形态的不同。在极端情况下,它会退化成一条链,这时使用BST的复杂度就退化成了\(O(mn)\)。(ps:vector在一般情况下也能以远低于\(O(mn)\)的复杂度完成以上操作)。
那该怎么办?用vector(
为了拯救Oier和BST,平衡树出现了。考虑到BST之所以会退化,是因为它在可能会变得非常“窄长”,于是,我们可以使用人为方式让BST保持宽宽扁扁的“好身材”,来保证复杂度为\(O(m\log n)\)这就是平衡树的由来。
平衡树可以分成不同的种类:
通过旋转操作实现平衡的:有旋Treap,Splay(伸展树),WBLT,AVL Tree,(左偏)红黑树
通过分裂与合并操作实现平衡的:FHQ Treap(无旋Treap)
通过暴力拍扁实现平衡的(害怕 :替罪羊树
由于本蒟蒻实在太蒻,只会Splay,因此就只跟大家讲Splay了
2.平衡?先得有树!
在开始splay之前,我们首先要准备一颗二叉树
如下:
#define maxn 100005
struct splayTree
{
int val, ch[2], fa, size, cnt;
} t[maxn];
int root, tot; //root是根结点的位置;tot是结点的数量,也是当前最后一个被插入的结点的编号
变量名的含义:
val : 该节点维护的权值
ls/rs:该结点左/右孩子的编号
fa: 该结点父亲的编号
size:以该结点为根的子树中的结点数
cnt:该结点的权值出现的次数
son,nxt:该结点nxt孩子的编号
我在代码中应用的一些宏如下
#define val(x) t[x].val
#define ls(x) t[x].ch[0]
#define rs(x) t[x].ch[1]
#define son(x, nxt) t[x].ch[nxt]
#define fa(x) t[x].fa
#define size(x) t[x].size
#define cnt(x) t[x].cnt
用了宏以后,我的代码虽然不是用指针写的,但是写法比指针还简洁
3.Rotate:向父亲进发!
正常来说,一个数据结构应该是以插入函数开始的。然而,splay的插入函数需要用到splay操作,因此就先从splay操作——的基础,rotate操作开始。
Rotate操作,也就是将儿子结点旋转到父亲结点的操作。如图,1,2,3是三个结点,4,5,6,7是四颗子树
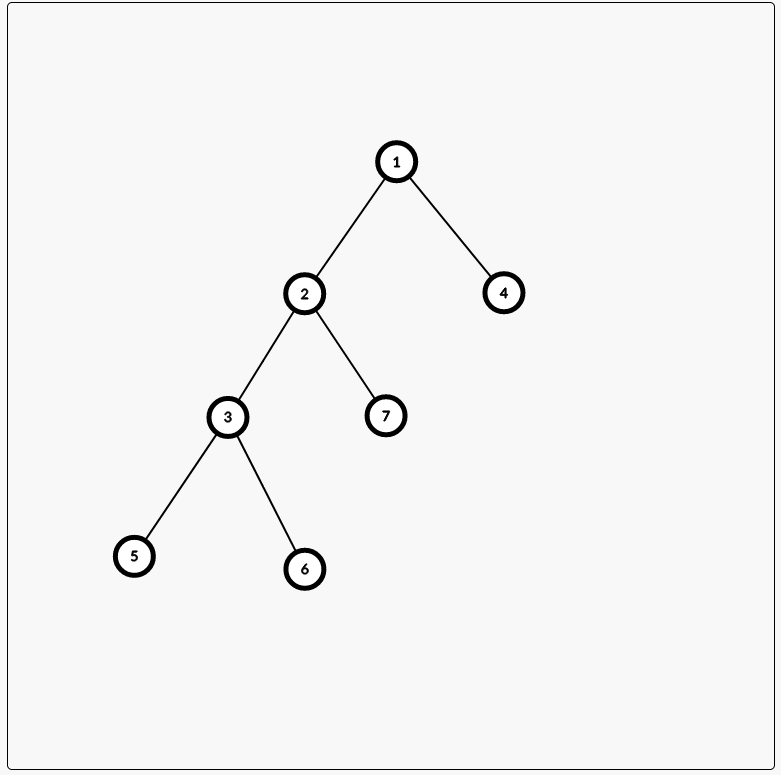
我们应该怎么操作,才能在不改变结点间大小关系(也就是中序遍历顺序)的情况下,将3旋转到2的位置上呢?
首先,我们有一个大小顺序:5<3<6<2<7<1<4,又因为6,5,7,4都是子树,不能向子树底部转移结点。我们把图拆成这种形式:
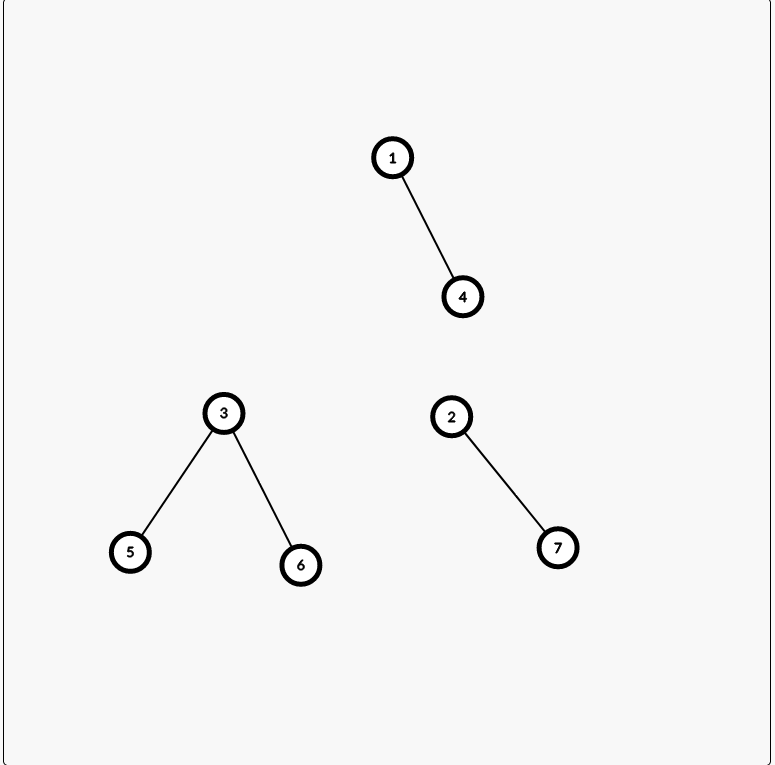
把3移到2的位置上,那么1,3必须连,2要找一个地方插进去,它只能把6子树挤掉,可6子树也要找一个位置插进去,此时2结点原先3结点在的位置有一个空缺,6子树就插了进去。这样以来,就能在不改变原先大小关系的情况下把3旋转到2的位置上。
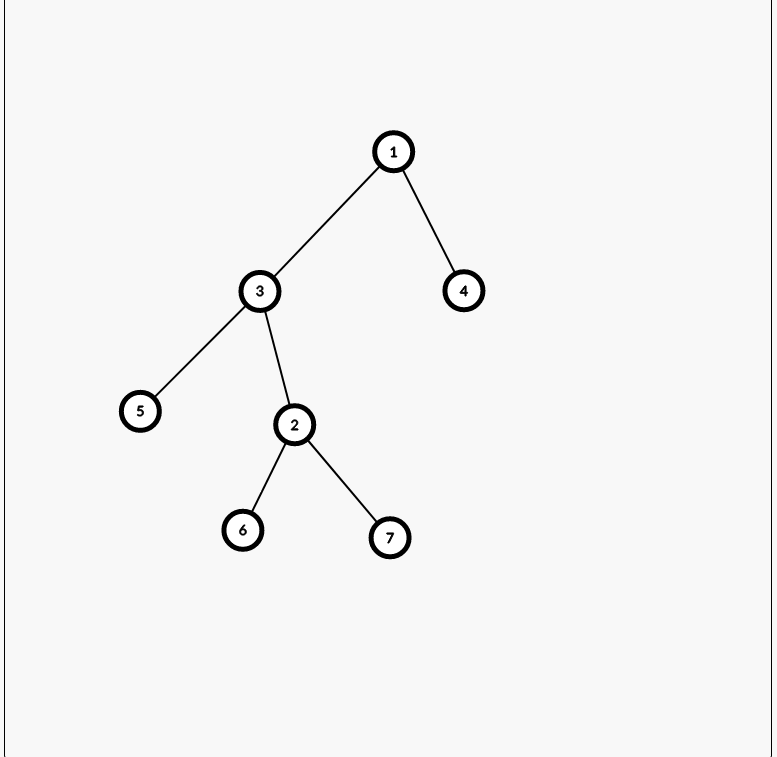
多次手模后,我们总结出了如下旋转的规则:
设要旋转到父亲的结点为x,它的父结点是y,祖父结点是z,x是y的fx孩子(0为左,1为右,下同),y是z的fy孩子
1.把x的fx^1孩子移动到y的fx孩子上
2.把y移动到x的fx^1孩子上
3.把x移动到z的y孩子上
最后,我们还要对y和x的size值进行pushup操作
代码如下:
pushup(int x) //更新父节点的size值
{
size(x) = size(ls(x)) + size(rs(x)) + cnt(x);
}
int ff(int x) //查询x是它父亲的哪一个节点
{
return rs(fa(x)) == x;
}
void connect(int x, int y, int nxt) //把x插入到y的nxt节点上
{
son(y, nxt) = x;
fa(x) = y;
}
void rotate(int x) //将x旋转到它父亲的位置
{
int y = fa(x), z = fa(y);
int fx = ff(x), fy = ff(y);
connect(son(x, fx ^ 1), y, fx);
connect(y, x, fx ^ 1);
connect(x, z, fy);
pushup(y), pushup(x);//从子结点向父结点上传
}
4.splay——旋转的艺术
经过前面的铺垫,我们终于来到了Splay最最核心的部分—— Splay。
splay操作,就是把一个点旋转到另一个点(一般是根节点)的位置。
虽然名字叫平衡树,但是splay降低依靠的并不是完全的平衡(AVL)。根据伟大的90-10法则,\(90\%\)的询问都发生在\(10\%\)的数据上。splay的原理就是:找到询问频率最高的结点,把旋转到根节点,以此在接下来的询问中提高效率。那什么是询问频率最高的点?这很难统计,但我们可以认为:你正在访问的点就是询问频率较高的点,把它旋到根节点就可以了。
那该如何进行splay呢?一个一个向上旋过去
我们十分容易就能想到,可以把x不停向上旋转,直到旋转到y。但这样做旋转的复杂度似乎会被卡到\(O(n)\)。事实上,有这么一个及其好记的结论
1.如果y是x的父亲,就让x向上单旋
2.如果x和x的父亲在树上偏的方向相同(都是左孩子或都是右孩子),就先让x的父亲向上单旋,在让x向上单旋
3.否则让x连续向上单旋两次
重复1,2,3条即可
代码如下:
void splay(int x, int y) //将x旋转到y的位置
{
y = fa(y);//先让y向上翻一个,判x的父亲是不是y,来避免一些奇奇怪怪的错误
while (fa(x) != y)
{
if (fa(fa(x)) == y)
rotate(x);
else if (ff(x) == ff(fa(x)))
rotate(fa(x)), rotate(x);
else
rotate(x), rotate(x);
}
if (y == 0)
{
root = x;//如果y是根结点,那现在根结点就变成了x
connect(x,0,1);
}
}
5.第一弹总结
值得注意的是,rotate和splay操作都没有改变结点间大小关系,更恰当的说这两个操作都与结点的权值完全无关。在我看来,splay的本质是维护了一个数列,这个数列就是splay的中序遍历。
我一般把平衡树分为两种:普通平衡树和文艺平衡树。
普通平衡树可以实现:第k大,前后驱,排名 等,它可以通过线段树套平衡树的方式实现区间内对上述元素的查询(树套树/二逼平衡树)。
文艺平衡树可以用来进行区间操作,例如区间修改,动态的RMQ,动态求区间最大字段和(山海经那题是静态的), 区间翻转(只此一家),区间平移(通过三次区间翻转实现)
我认为:普通平衡树和文艺平衡树的本质不同在于,普通平衡树严格按照BST的定义,它的中序遍历是始终单调递增的。而文艺平衡树以编号作为权值,编号间大小关系是因区间翻转而不断被重定义的,它的中序遍历也因此不断发生变化。
这些内容我会在第四弹详细讲到。
第二弹讲完普通平衡树。争取在后天有奥赛课时更新。
最后的最后,贞德老婆镇楼。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号