【STM32F429的DSP教程】第27章 FFT的示波器应用
完整版教程下载地址:http://www.armbbs.cn/forum.php?mod=viewthread&tid=94547
第27章 FFT的示波器应用
特别声明:本章节内容整理自力科示波器基础应用系列文档,原名《FFT的前世今生》。
FFT(Fast Fourier Transform,快速傅立叶变换)是离散傅立叶变换的快速算法,也是我们在数字信号处理技术中经常会提到的一个概念。在大学的理工科课程中,完成高等数学的课程后,数字信号处理一般会作为通信电子类专业的专业基础课程进行学习, 原因是其中涉及了大量的高等数学的理论推导,同时又是各类应用技术的理论基础。关于傅立叶变换的经典著作和文章非常多,但是看到满篇的复杂公式推导和罗列,我们还是很难从直观上去理解这一复杂的概念, 对于普通的测试工程师来说,掌握 FFT的概念首先应该搞清楚这样几个问题(在这篇文章中尝试用更加浅显的讲解,尽量不使用公式推导来说一说 FFT 的那些事儿):
27.1 初学者重要提示
27.2 傅里叶变换的物理意义
27.3 FFT变换是如何进行的
27.4 FFT变换前后有何种对应关系
27.5 使用示波器进行 FFT 的方法和需要注意的问题
27.6 力科示波器与Tek示波器的 FFT 计算方法的比较
27.7 珊栏现象
27.8 窗函数对于FFT结果的影响
27.9 窗函数选择指南
27.10 总结
27.1 初学者重要提示
- 本章的知识点非常重要,强烈推荐初学者学习下,尤其注意两个关键知识点频谱泄露和栅栏效应。
27.2 傅里叶变换的物理意义
傅立叶原理表明:任何连续测量的时序或信号, 都可以表示为不同频率的正弦波信号的无限叠加。 而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号,以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。当然这是从数学的角度去看傅立叶变换。
那么从物理的角度去看待傅立叶变换,它其实是帮助我们改变传统的时间域分析信号的方法转到从频率域分析问题的思维,下面的一幅立体图形可以帮助我们更好得理解这种角度的转换:
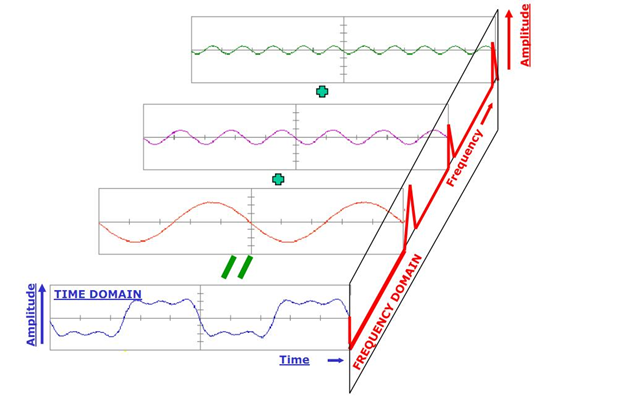
所以,最前面的时域信号在经过傅立叶变换的分解之后,变为了不同正弦波信号的叠加,我们再去分析这些正弦波的频率,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
傅立叶变换提供给我们这种换一个角度看问题的工具,看问题的角度不同了,问题也许就迎刃而解!
27.3 FFT变换是如何进行的
首先,按照被变换的输入信号类型不同,傅立叶变换可以分为 4 种类型:
1、 非周期性连续信号傅立叶变换(Fourier Transform)
2、 周期性连续信号傅立叶级数(Fourier Series)
3、 非周期性离散信号离散时域傅立叶变换(Discrete Time Fourier Transform)
4、 周期性离散信号离散傅立叶变换(Discrete Fourier Transform)
下面是四种原信号图例:
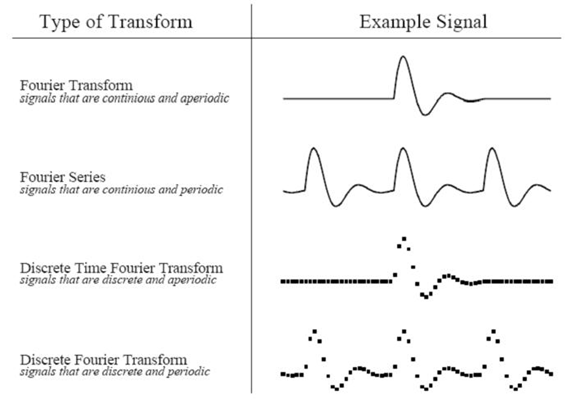
这里我们要讨论是离散信号, 对于连续信号我们不作讨论, 因为计算机只能处理离散的数值信号,我们的最终目的是运用计算机来处理信号的。所以对于离散信号的变换只有离散傅立叶变换(DFT)才能被适用,对于计算机来说只有离散的和有限长度的数据才能被处理,对于其它的变换类型只有在数学演算中才能用到,在计算机面前我们只能用 DFT方法,我们要讨论的 FFT 也只不过是 DFT 的一种快速的算法。DFT 的运算过程是这样的:

X(k)—频域值
X(n)—时域采样点
n—时域采样点的序列索引
k—频域值的索引
N—进行转换的采样点数量
可见,在计算机或者示波器上进行的 DFT,使用的输入值是数字示波器经过 ADC后采集到的采样值,也就是时域的信号值,输入采样点的数量决定了转换的计算规模。变换后的频谱输出包含同样数量的采样点, 但是其中有一半的值是冗余的, 通常不会显示在频谱中,所以真正有用的信息是 N/2+1 个点。FFT 的过程大大简化了在计算机中进行 DFT 的过程,简单来说, 如果原来计算 DFT的复杂度是N2次运算 (N 代表输入采样点的数量), 进行 FFT 的运算复杂度是:

因此,计算一个 1,000 采样点的 DFT,使用 FFT 算法只需要计算 3,000 次,而常规的 DFT算法 需要计算 1,000,000 次!
我们以一个 4 个点的 DFT 变换为例来简单说明 FFT 是怎样实现快速算法的:
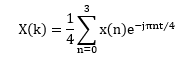
计算得出:
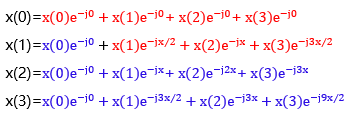
其中的红色部分在FFT中是必须计算的分量,其它蓝色部分不需要直接计算,可以由红色的分量直接推导得到,比如:
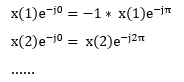
这样, 已经计算出的红色分量只需要计算机将结果保存下来用于之后计算时调用即可, 因此大大减少了 DFT 的计算量。
27.4 FFT变换前后有何种对应关系
我们以一个实际的信号为例来说明:
示波器采样得到的数字信号,就可以做 FFT 变换了。N 个采样点,经过 FFT 之后,就可以得到 N 个点的 FFT 结果。为了方便进行 FFT 运算,通常 N 取 2 的整数次方。假设采样频率为 Fs, 信号频率 F, 采样点数为 N。 那么 FFT 之后结果就是一个为 N点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的 幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为 A,那么 FFT 的结果的每个点(除了第一个点直流分量之外)的模值就是 A 的 N/2 倍。 而第一个点就是直流分量,它的模值就是直流分量的 N 倍。而每个点的相位呢,就是在该频率下的信号的相位。第一个点表示直流分量(即 0Hz) ,而最后一个点 N 的再下一个点(实际上这个点是不存在的, 这里是假设的第 N+1 个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率 Fs,这中间被 N-1 个点平均分成 N 等份,每个点的频率依次增加。例如某点 n 所表示的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn 所能分辨到频率为 为 Fs/N,如果采样频率 Fs 为 1024Hz,采样点数为 1024 点,则可以分辨到 1Hz。1024Hz 的采样率采样 1024 点,刚好是 1 秒,也就是说, 采样 1 秒时间的信号并做 FFT,则结果可以分析精确到 1Hz,如果采样 2 秒时间的信号并做 FFT,则结果可以分析精确到 0.5Hz。如果要提高频率分辨率,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
下面这幅图更能够清晰地表示这种对应关系:
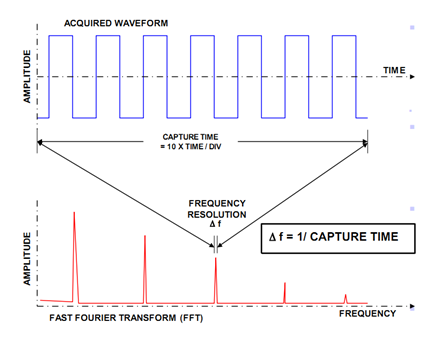
变换之后的频谱的宽度(Frequency Span)与原始信号也存在一定的对应关系。根据 Nyquist 采样定理,FFT 之后的频谱宽度(Frequency Span)最大只能是原始信号采样率的 1/2,如果原始信号采样率是 4GS/s,那么 FFT 之后的频宽最多只能是 2GHz。时域信号采样周期 (Sample Period)的倒数,即采样率(Sample Rate)乘上一个固定的系数即是变换之后频谱的宽度,即 Frequency Span = K*(1/ΔT) ,其中ΔT 为采样周期,K 值取决于我们在进行 FFT 之前是否对原始信号进行降采样(抽点) ,因为这样可以降低 FFT 的运算量。如下图所示:
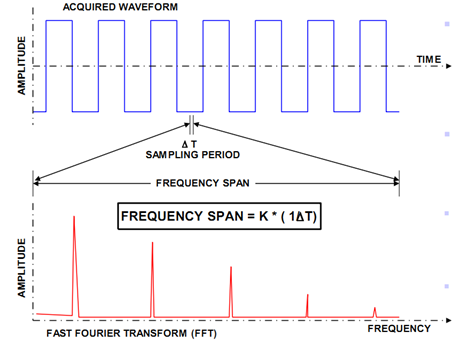
可见, 更高的频谱分辨率要求有更长的采样时间, 更宽的频谱分布需要提高对于原始信号的采样率,当然我们希望频谱更宽,分辨率更精确,那么示波器的长存储就 是必要的!它能提供您在高采样率下采集更长时间信号的能力!值得强调的是,力科示波器可以支持计算 128Mpts 的 FFT,而其它某品牌则只有 3.2Mpts。
27.5 使用示波器进行 FFT 的方法和需要注意的问题
我们先来看一个简单的例子:
Problem:在示波器上采集一个连续的,周期性的信号,我们希望在示波器上进行 FFT 计算之后, 观察到信号中心频率 (Center Frequency) 在 2.48GHz, 频宽 (Frequency Span) 为 5MHz,频谱分辨率(Bandwidth Resolution)为 10KHz 的频谱图,应该如何设置示波器的采集?
首先,根据频谱分辨率(Bandwidth Resolution)10KHz 可以推算出,至少需要采集信号的时间长度为 1/10KHz=100us, 因此至少要设置示波器时基为 10us/Div; 为了尽量保证 FFT 之后频谱图在各个频点的信号能量精度,测量时需要时域信号幅值占满整个栅格的90%以上;采样率设置应至少满足 Nyquist 采样率,即至少设置 >5GS/s 采样率才能够看到中心频率在 2.48GHz 的频率谱线;选择合适的窗函数(Von Hann 汉宁窗)和频谱显示方式(power spectrum);使用 Zoom 工具,将频谱移动到 Center 2.48GHz,Scale 500KHz/Div 位置,Zoom 设置方法如下图所示:

在力科示波器中进行 FFT 的运算有几种不同的输出类型:
Linear Magnitude(Volts),
Phase(Degrees),
Power Spectrum(dBm),
Power Spectral Density(dBm)
这几种输出类型都是由 FFT 计算之后的结果换算而来,我们知道 FFT 计算之后的结果包含实部(Real)和虚部(Imaginary)成分,它们的单位都是 Volts。具体的换算方式如下:
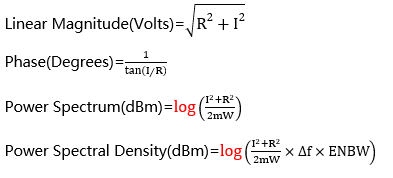
其中ΔF为频谱分辨率,ENBW为与所选加权函数(窗)相关的有效噪声带宽。
几种典型周期函数的频谱图:
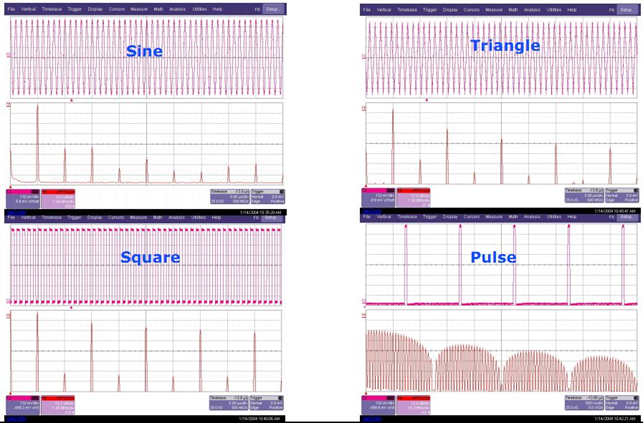
频谱泄露:
所谓频谱泄露,就是信号频谱中各谱线之间相互干扰,使测量的结果偏离实际值,同时在真实谱线的两侧的其它频率点上出现一些幅值较小的假谱。产生频谱泄露的主要原因是采样频率和原始信号频率不同步,造成周期的采样信号的相位在始端和终端不连续。 简单来说就是因为计算机的 FFT 运算能力有限,只能处理有限点数的FFT,所以在截取时域的周期信号时,没有能够截取整数倍的周期。信号分析时不可能取无限大的样本。只要有截断不同步就会有泄露。如下图所示:

图中被测信号的开始端相位和截止端相位相同, 表示在采集时间内有整数倍周期的信号被采集到,所以此时经行 FFT 运算后得出的频谱不会出现泄露。
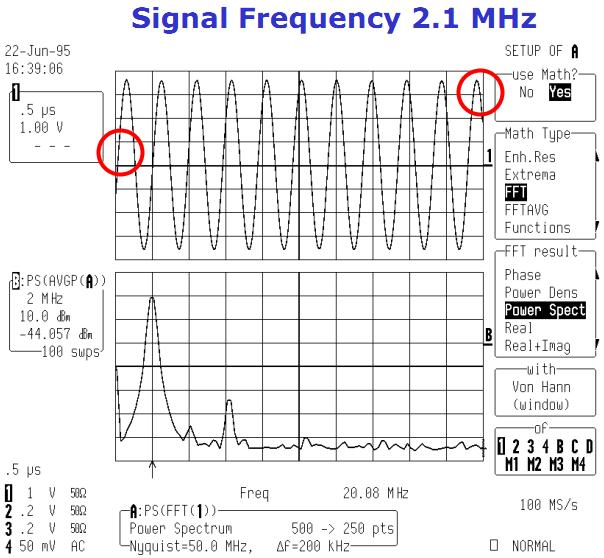
上图的信号频率为 2.1MHz,采集时间内没有截取整数倍周期的信号,FFT 运算之后谱线的泄露现象严重,可以看到能量较低的谱线很容易被临近的能量较高的谱线的泄露给淹没住。
因此,避免频谱泄露的方法除了尽量使采集速率与信号频率同步之外,还可以采用适当的窗函数。
另外一个方法是采集信号时间足够长,基本上可以覆盖到整个有效信号的时间跨度。这种方法经常在瞬态捕捉中被使用到,比如说冲击试验,如果捕捉的时间够长,捕捉到的信号可以一直包括了振动衰减为零的时刻。在这种情况下,可以不加窗函数。窗函数其实就是一个加权函数,它在截取的信号时间段内有值,时间段之外值为 0:,记为:
w(t)=g(t) -T/2<t<T/2
w(t)=0 其它
加窗在时域上表现的是点乘,因此在频域上则表现为卷积。卷积可以被看成是一个平滑的过程。这个平滑过程可以被看出是由一组具有特定函数形状的滤波器,因此,原始信号中在某一频率点上的能量会结合滤波器的形状表现出来,从而减小泄漏。基于这个原理,人们通常在时域上直接加窗。
大多数的信号分析仪一般使用矩形窗(rectangular),汉宁(hann),flattop 和其它的一些窗函数。
不同的窗函数对频谱谱线的影响不同,基本形状可以参看下图:
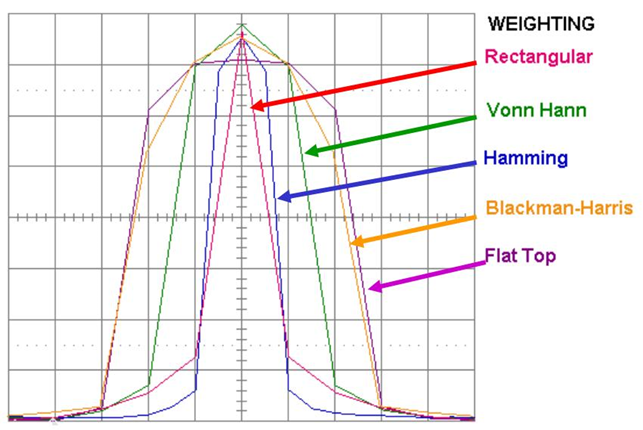
可以看到,不同的窗函数的主瓣宽度和旁瓣的衰减速度都不一样,所以对于不同信号的频谱应该使用适当的窗函数进行处理。
矩形窗(Rectangular):加矩形窗等于不加窗,因为在截取时域信号时本身就是采用矩形截取,所以矩形窗适用于瞬态变化的信号,只要采集的时间足够长,信号宽度基本可以覆盖整个有效的瞬态部分。
汉宁窗(Von Hann):如果测试信号有多个频率分量,频谱表现的十分复杂,且测试的目的更多关注频率点而非能量的大小。在这种情况下,需要选择一个主瓣够窄的窗函数,汉宁窗是一个很好的选择。
flattop窗:如果测试的目的更多的关注某周期信号频率点的能量值,比如,更关心其EUpeak, EUpeak-peak, EUrms,那么其幅度的准确性则更加的重要,可以选择一个主瓣稍宽的窗,flattop窗在这样的情况下经常被使用。
27.6 力科示波器和Tek示波器的FFT计算方法的比较
您可能也已经发现了这个问题:在示波器上进行 FFT 运算时,使用力科示波器和使用 Tek 示波器的计算结果似乎相差很大。产生这种差别的原因一方面可能是两者有效运算的采样点不一样。另外一个重要原因是 LeCroy 和 Tek 所使用的 FFT 运算的参考值不同,LeCroy 使用 dBm 为单位(参考值是 1mW 的功 率值),而 Tek 使用 dB 为单位(参考值是1V rms 的电压值),参考值不同产生的计算结果当然不一样!
dB(Deci-bel, 分贝) 是一个纯计数单位,本意是表示两个量的比值大小,没有单位。在工程应用中经常看到貌似不同的定义方式(仅仅是看上去不同)。对于功率,dB =10*lg(A/B)。对于电压或电流,dB = 20*lg(A/B)。此处 A,B 代表参与比较的功率值或者电流、电压值。dB 的意义其实再简单不过了,就是把一个很大(后面跟一长串0的)或者很小(前面有一长串0 的)的数比较简短地表示出来。dBm是一个考征功率绝对值的值,计算公式为:10lg(功率值/1mw) 。
此外,还有 dBV、dBuV、dBW 等等,仅仅是参考值选择的不同而已。如下是一个实测的例子,使用同一信号分别用 LeCroy 和 Tek 示波器进行FFT运算,下图是使用 LeCroy WaveRunner 64Xi 的测试结果:
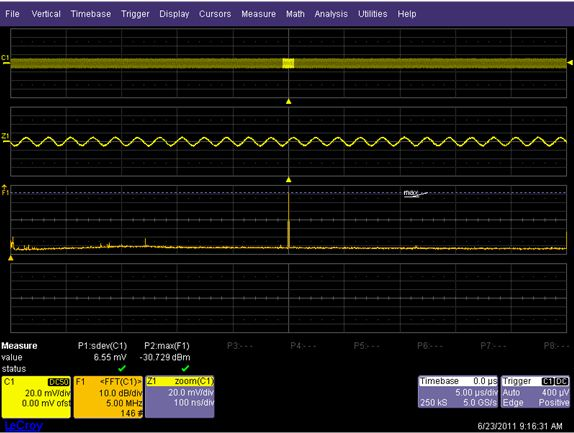
下图是使用 Tek DPO4104 的测试结果:
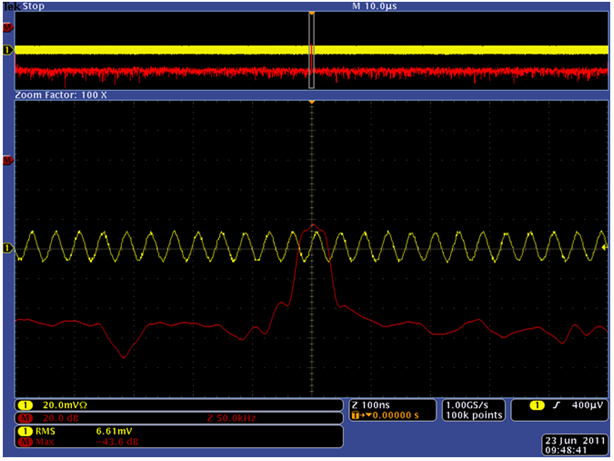
测试所使用的信号幅值是 6.55 mV rms , 信号频率是 25 MHz
力科使用的计算方式如下:
dBm = 10 Log10 (((vrms^2)/50)/0.001)= 10Log10 ((4.29E-5/50)/0.001)=
10Log10(8.5E-7/0.001)=10Log10 (8.5e-4)=10 (-3.066)= -30.66dBm
Tek 使用的计算方式如下:
dB= 20Lg (6.61E-3)= 10(-4.3596)=-43.59
换算关系如下:


不仅仅只是 FFT 计算方式的差别,我们以力科的 WaveMaster 8Zi-A 和 Tek 的DPO70000 系列为例,在 WaveMaster 上您可以做最多 128M 个采样点的 FFT 运算,而在DPO70000 上只能做 3.2M 个点的 FFT 运算,所以,这种差别才是本质上的!
27.7 栅栏现象
从直观上讲,时域分析清晰易见,示波器即是进行时域观察的主要工具,可观察波形形状,测量脉宽,
相差等信息。但对于信号的进一步分析,比如测量各次谐波在所占的比重和能量分布,时域上的分析就力不从心了,但是利用从连续时间傅里叶变换发展而来的快速傅里叶变换FFT进行分析就很有意义了。通信系统中必不可少的要使用频谱分析技术,例如频分复用技术。频谱分析一般利用快速傅里叶变换 FFT计算频率谱和功率谱,可直接用来提取特征频率和谱特征。因为计算机只能够处理离散的数据点,但 FFT是傅里叶变换的一种近似,与傅里叶变换存在差别,且具有固有的局限:栅栏现象。本小节就是在上面小节的基础上,从测试测量的角度,谈一谈在示波器的 FFT 运算中容易被大家忽略的一些问题。
27.7.1 频率分辨率与时基设置(TimeBase)
频率分辨率的定义是:在使用 FFT 运算时,在频率谱上所能得到的最小的两个频率点间的间隔。
ΔF=Fs/N=1/NT=1/Tp
称ΔF 为频率分辨率,即:采样率/采样点数,ΔF 越小说明频率分辨率越高。∆F 仅与信号的实际长度成反比,即待分析的信号持续时间越长,ΔF 越小,频率分辨率越高。
27.7.2 栅栏效应与频率分辨率
示波器输入的信号一般都为非周期的连续信号 ,它的频谱也是连续的,但是示波器所做的工作是将 进行等间隔采样并且截断,然后进行 FFT 的运算得到一个离散的频谱图,相当于对连续的频谱图也进行了采样。这样有一部分频谱分量将被“挡在”采样点之外,就好像我们在通过一个栅栏观察频谱图,这种现象称为“栅栏效应”。这样就有可能发生一些频谱的峰点或谷点被栅栏所拦住,不可能被我们观察到。
不管是时域采样还是频域采样,都有相应的栅栏效应。只是当时域采样满足采样定理时,栅栏效应不会有什么影响。而频域采样的栅栏效应则影响很大,“挡住”或丢失的频率成分有可能是重要的或具有特征的成分,使信号处理失去意义。
栅栏效应是制约频谱分析谐波分析精度的一个瓶颈。栅栏效应在非同步采样的时候,影响尤为严重。
在非同步采样时,由于各次谐波分量并未能正好落在频率分辨点上,而是落在两个频率分辨点之间。这样通过 FFT 不能直接得到各次谐波分量的准确值,而只能以临近的频率分辨点的值来近似代替,这就是栅栏效应降低频谱分析精度的原因。
由此我们可以得出这样的结论:减小栅栏效应可用通过提高频谱采样间隔也就是频率分辨率的方法来解决。间隔小,频率分辨率高,被“挡住”或丢失的频率成分就会越少。但是频率分辨率的提高会增加采样点数,使计算工作量增加。
我们可以通过两种方式增加频率分辨率:
a:物理分辨率=采样频率/采样点数。
物理分辨率的实际意义在于它可以衡量FFT实际上可以区分的频率分量的间隔。提高物理分辨率的方法一般是通过增加数据的有效长度,这相当于在模拟域增加了矩形窗的宽度。从而在模拟域减小了sinc主旁瓣宽度,减小了相邻频率分量的混叠。
这种增加采样点的方法主要针对无限长序列的FFT计算。对于无限长序列,不像有限长序列那样必须补零来提高视在分辨率,无限长序列可以通过增加数据长度来提高物理分辨率。
b:视在分辨率=采样频率/分析点数
在序列尾部补零的方法可以使得分析点数增大,故补零的方法可以提高频谱的视在分辨率。对序列的尾部补零的方法主要针对有限长序列。对于有限长序列,有时只能用补零或者插值来改善频率分辨率。
通过补零处理,使得频域采样密度增大,得到高密度谱。补零的方法所得到的频谱图所改善的只是图形
的视在分辨率,并不能得到频谱的更多细节。增加采样点数,增加了输入序列的阶次,从而提供频谱的更多细节,这是真正的分辨率(物理分辨率)。对序列只补零而不增加数据,输入序列和它的频谱阶次依旧没有提高,只是把频谱画的密一些,所以改善的只是图形的视在分辨率,并不能得到频谱的更多细节。增加序列的长度能够改善频谱的真正分辨率,这是基本的规律。
上面的讨论可知,改善分辨率的具体方法有如下两种
(1)对有限长序列采取尾部补零的方法提高视在分辨率
(2)对无限长序列通过真正增加采样点来提高物理分辨率
有限长序列和无限长序列是针对实际信号来说的,例如非周期的但是包含无限长信息的信号可以称为无限长序列,严格的周期信号和脉冲信号(脉冲之前和之后无限长时间内都是无效信息)都可以称为有限长序列,当然实际上严格的周期信号是不存在的。对于示波器来说,时间窗口内采集到的可以是有限长序列的全部信息或者是无限长序列的一部分信息。所以,如果采集到的是有限长序列的全部信息,那么只能通过补零的方式增加视在分辨率,如果采集到的是无限长序列的一部分信息,那么可以通过增加时间窗口的长度(不是采样点)来增加物理频率分辨率。
请看下面的实例:
图1中正弦波测试使用的时基是 5ns/div,波形时间长度是 50ns,计算 FFT 之后的频谱分辨率是 20MHz(1/50ns)
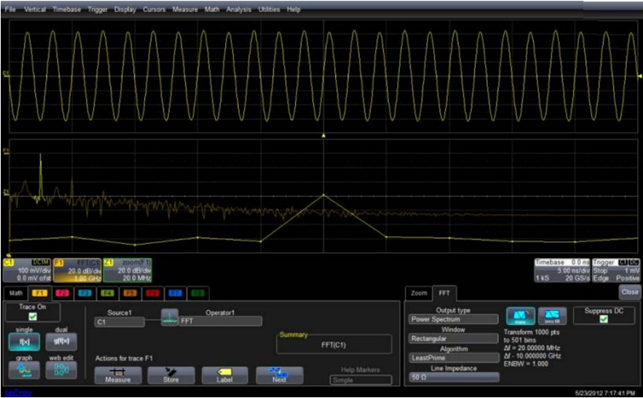
图 1 捕获 50ns 的信号,频率分辨率是 20MHz
如果改变时基设置,频谱分辨率会有变化。如图2所示:将时基设置为10ns/div,波形长度是100ns,频谱分辨率可以提高到10MHz。
对于通过补零的方法增加FFT频谱的视在分辨率,力科的示波器也有相应的解决方案。力科示波器使用了两种非常常用的FFT算法供用户选择:Cooley-Tukey算法和LeastPrime算法。Cooley-Tukey算法也称为Power2算法,它提供了计算机一种非常快速的FFT计算方式,计算的FFT点数规模是2的整数方次,因此它会在示波器时域采集的信号中截取2的N次方的整数来作为FFT计算的时域样本,该截取的整数是最接近于采样点的整数。如下图2所示:
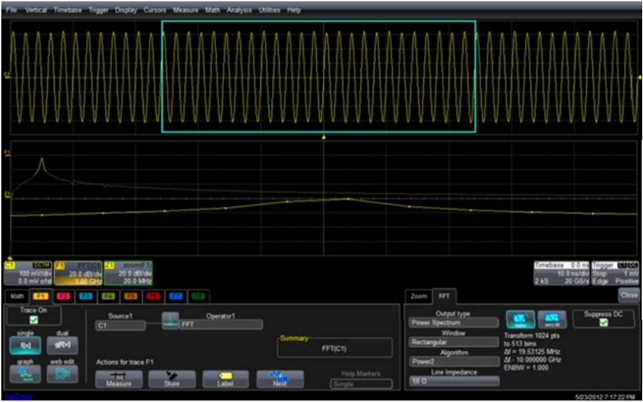
图 2 捕获 100ns 的信号,频率分辨率是 10MHz
图中的正弦波频率为 500MHz,时基设置为 10ns/div,采样率为 20GS/s,时域采样点数为 2000points,
使用 Power2 算法截取 2000 点中的 1024 点(210),如图中的蓝框所示(注意是从信号的中间部分截取),因此截取的时间窗口为 1024×20ps=51.2ns,是 500MHz 信号的 25.6 个周期,由于截取的周期非整数倍,不可避免会产生频谱泄露,如图中 FFT 的旁瓣所示,此时的频率分辨率可以达到 19.35125MHz。
如果采用另外一种 FFT 算法 LeastPrime,可以将整个示波器时域采集的采样点进行 FFT 运算, LeastPrime算法计算的 FFT 点数规模是 2N+5K,因此 2000 点=24+53,不需要截取原始数据就可以运算,但是代价是计算的速度可能会慢一些(尽管我们可能觉察不到),频率分辨率可以提高到 10MHz。使用 Power2 算法也可以不采用截取原始波形的方式,此时我们可以选择 Zero Fill(补零)的方式,增加采样点数。比如,在 2000 点中补 48 个点,2048=211,如图 3 所示:
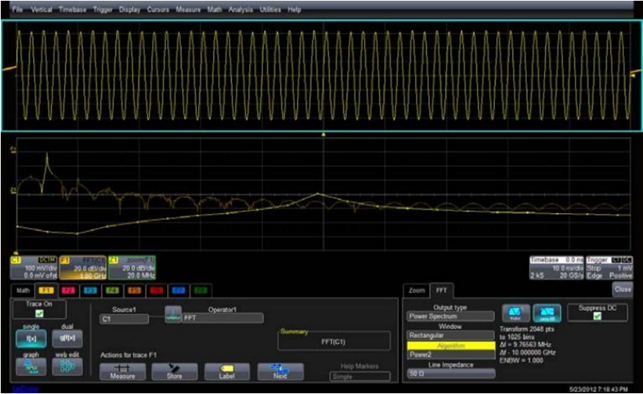
图 3 补零的放出提高频率分辨率
这 48 个点补的方式是头尾各补一半,但是有可能补的不是 0,头 24 个点与第一个采样点值相同,尾24 个点与最后一个采样点值相同(所以称之为 Zero Fill 是不完全准确的)。这里我们推荐 Zero Fill 的方法只在分析冲击信号FFT频谱的情况下使用。
补零法虽然能增加频谱图的视在分辨率,但是由于补的都是无效数据,所以对于频率分辨率真正的改善没有帮助,但是补零有它的好处:
- 补零后,其实是对 FFT 结果做了插值,克服“栅栏”效应,使谱外观平滑化;我把“栅栏”效应形象理解为,就像站在栅栏旁边透过栅栏看外面风景,肯定有被栅栏挡住比较多风景,此时就可能漏掉较大频域分量,但是补零以后,相当于你站远了,改变了栅栏密度,风景就看的越来越清楚了。
- 由于对时域数据的截短必然造成频谱泄露,因此在频谱中可能出现难以辨认的谱峰,补零在一定程度上能消除这种现象。除此之外,很多人都有这样的误区:认为通过增加待分析的计算点数而不是增加采样时间就可以使FFT 之后的频谱更加“精细”(频率分辨率更高)。这样的误解一般来自于示波器的用户,因为当示波器采样点比较少时,FFT 的计算出来的频谱图也会很少,频谱看起来非常粗糙。这时工程师会非常有冲动把时域的采样点增多(用示波器上的插值算法很容易实现),但是如果采集信号的时间长度是不变的,工程师会发现 FFT 计算之后的频谱并没有显得更加“精细”,频率分辨率并没有任何改善。实际上使用插值或者增加采样率的方式仅仅是展宽了 FFT 之后的频谱带宽。如下图 4 所示:

图 4 插值方式并不能改变频率分辨率
左上方使用了较少的时域采样点C1,右上方使用了较高的采样率C2,但是采样时间是相同的。左下是对 C1 进行 FFT 之后的频谱F1,右中是对C2 进行FFT之后的频谱F2,右下是对F2相同频段进行了放大。可以看到 F2 比 F1 的频宽增加了,但是对 F1 频段放大之后的频谱和 F1 一样,没有任频率分辨率的改善。
由此我们可以得出结论,对 C1 进行插值后,额外的采样点仅仅存在于较高频段,会展宽频谱的带宽,但是插值方式对于增加我们感兴趣频段的频谱分辨率没有任何帮助。
那么如果我们只对对FFT之后的频谱进行插值效果如何呢?如下图 5 所示:
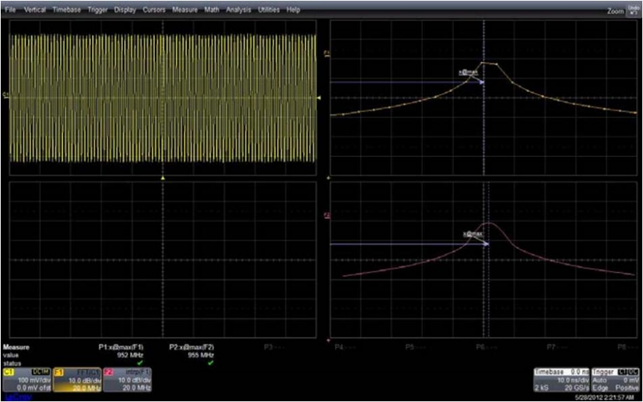
图 5 频域插值方式是频谱图看起来更密
图中展示了对频域插值之后的效果,并没有使频谱看起来更“窄”(毕竟插值出来的点都是假点),但是我们注意到,频域插值可以使频谱的测量更加精确。图中正弦波的频率是 955MHz,插值之后频谱的 Peak 频率读数 P2 是 955MHz,插值之前 P1 的读数为 952MHz。
总之, FFT 是进行信号频域分析的最广泛使用的标准化方法,也是现代数字示波器中标配的数学运算函数, 我们更多了解 FFT 应用的细节,能更加有效地利用好这个工具, 从 FFT 中得到更多有价值的信息。
27.8 窗函数对于FFT结果的影响
所谓频谱泄露,就是信号频谱中各谱线之间相互干扰,使测量的结果偏离实际值,同时在真实谱线的两侧的其它频率点上出现一些幅值较小的假谱。产生频谱泄露的主要原因是采样频率和原始信号频率不同步,造成周期的采样信号的相位在始端和终端不连续。简单来说就是因为计算机的FFT运算能力有限,只能处理有限点数的 FFT,所以在截取时域的周期信号时,没有能够截取整数倍的周期。信号分析时不可能取无限大的样本。只要有截断不同步就会有泄露。
在图6和图7中,为了最大化 FFT 运算之后的频率分辨率,我们使用了矩形窗。图中的时域信号是500MHz 正弦波信号,在频谱上应该仅在 500MHz 频点上看到谱线。FFT 运算研究的是整个时间域(-∞,+∞)与频域的关系,所以对于矩形窗函数截取的波形应该认为是无穷延续的,因此,矩形窗 100ns 时间窗内,包含了 500MHz 正弦波整 50 个周期,所以波形的首尾能够整周期得无缝连接,FFT 之后的频谱会在 500MHz 频点看到较为纯净的能量值。如下图6所示
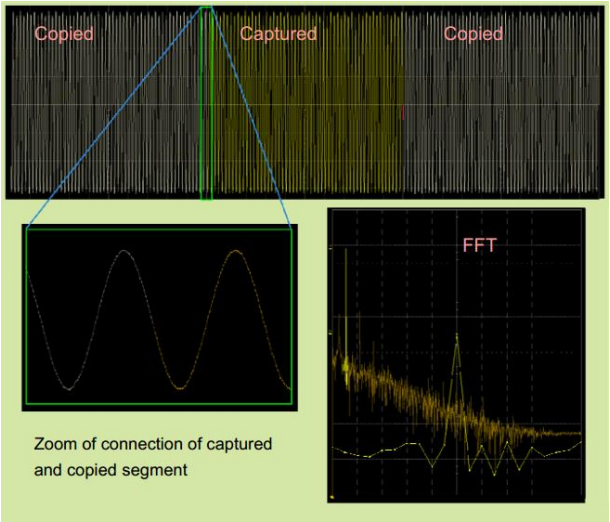
图 6:矩形时间窗口内包含整数倍周期的信号,首尾可以“无缝”连接
事实上,大多数类型的信号都不满足上面的这种特殊情况,绝大多数信号在时间窗口内都不是整周期的倍数,在这种情况下,FFT 之后的频谱就不能看做连续的正弦波了。例如,如果该正弦波的频率是495MHz,在 100ns 时间窗口内包含 49.5 个周期,因此在截取窗口的首尾部分就存在很大程度上的“不连续”,这种“不连续”会直接影响 FFT 之后的结果。“不连续”部分的能量会散落在整个频谱范围内,使用100ns 时间窗口,FFT 之后的频率分辨率是 10MHz,495MHz 频点即落在 490MHz 与 500MHz 之间,所以495MHz 正弦波信号的能量分成两部分,所以从频谱上看,峰值谱线明显降低了,这被称作是频谱泄露(Leakage)。如下图7所示:
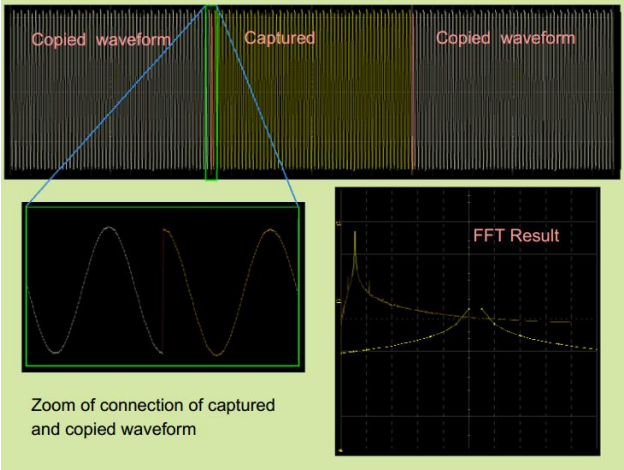
图 7:对于非整数倍周期信号进行 FFT 运算的效果
不同的窗函数对信号频谱的影响是不一样的,这主要是因为不同的窗函数,产生泄漏的大小不一样,
频率分辨能力也不一样。信号的截短产生了能量泄漏,而用FFT算法计算频谱又产生了栅栏效应,从原理上讲这两种误差都是不能消除的,但是我们可以通过选择不同的窗函数对它们的影响进行抑制。(矩形窗主瓣窄,旁瓣大,频率识别精度最高,幅值识别精度最低;布莱克曼窗主瓣宽,旁瓣小,频率识别精度最低,但幅值识别精度最高)
为了减少频谱旁瓣和栅栏效应的影响, 我们在 FFT 运算中使用窗函数,图8显示了 Hanning (汉宁窗)使用后的效果。窗函数位于下图中左上角的栅格中红色的波形,叠加在黄色的时域信号上。窗函数与时域信号时域相乘。结果显示在左下角的蓝色波形。右下角的粉色波形显示了进行 FFT 计算之后的频谱图,相对于右上角的使用窗函数之前的频谱图来说,旁瓣的幅度已经大大减低。
对于不同的应用需求还有多种不同的窗函数供工程师选择,Hanning(汉宁窗)是使用最广泛的一种窗函数,除此之外,Hamming(海明窗),Flat-top 窗和 Balckman-Harris 窗的效果,在下图中做了对比,图中的信号使用 500MHz 正弦波,矩形窗产生最窄的谱线,加 Flat-top 窗谱线最宽。
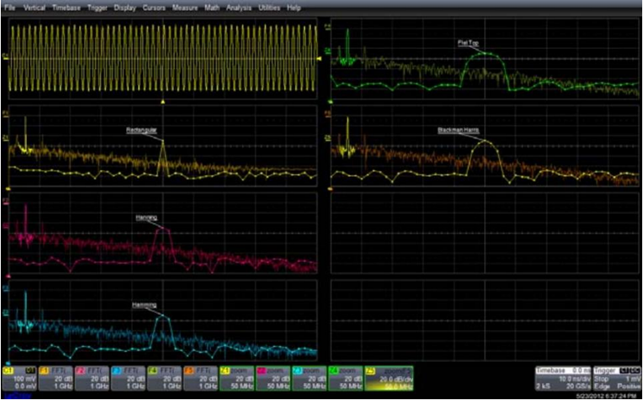
图8: 500MHz 正弦波频谱在不同窗函数下的对比
下图9中显示了同样的窗函数对比,但是采用 495MHz 正弦波进行 FFT 运算,矩形窗显示了最差旁瓣效果,Flat-top 窗函数基本上保持了与图8一样的旁瓣效果,所以我们看到旁瓣的影响和精确频率分辨率有时候是不可兼得的。(矩形窗主瓣窄,旁瓣大,频率识别精度最高,幅值识别精度最低;Flat-top 窗主瓣宽,旁瓣小,频率识别精度最低,但幅值识别精度最高)。
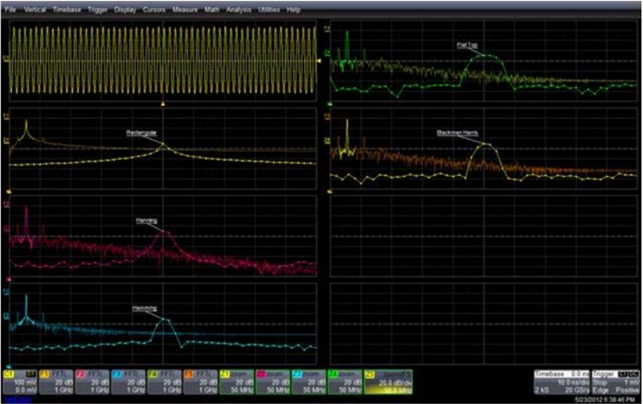
图 9:495MHz 正弦波频谱在不同窗函数下的对比
图 10 中显示了不同的窗函数对于栅栏效应的抑制效果,图中的正弦波频率从 450MHz 增加到 550MHz,步进值为 500KHz,Flat-top 窗在整个频段上基本保持相同的值,矩形窗函数有约 4dB 的差值。
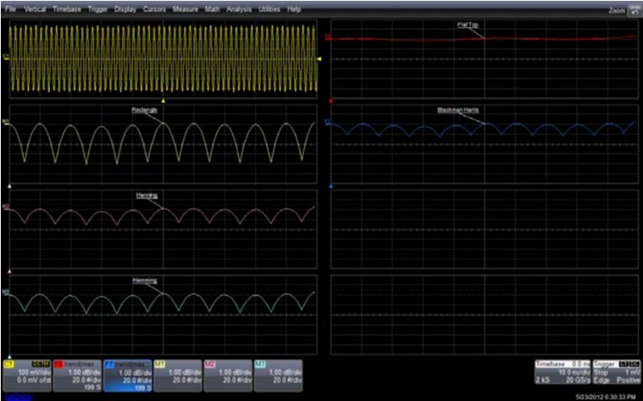
图10:从 500MHz 到 600MHz,不同窗函数的峰值变化
我们把关于窗函数的一些重要的结论总结如下:
1、 连续的 FFT 运算并没有窗函数的概念,因为信号是充满时间坐标轴的,FFT 之后的频率分辨率是0,并不存在栅栏效应。但是,示波器采集和处理的信号全部是离散的采样点,是非连续的,所以 DFT 之后的频谱一定存在栅栏效应。
2、 如果能够保证示波器时间窗口内的信号是整数倍周期的(并且在信号时间窗口之前和之后的信号都是严格周期重复的),或者采集信号时间足够长,基本上可以覆盖到整个有效信号的时间跨度。这种方法经常在瞬态捕捉中被使用到,比如说冲击试验,如果捕捉的时间够长,捕捉到的信号可以一直包括了振动衰减为零的时刻。在这种情况下,可以不加窗函数。
3、 如果不满足 1 和 2,那么 FFT 计算之后的频谱就不可避免受到频谱泄露(Leakage)的影响,如频点分裂,幅值能量不精确等等,总之就是频谱线比较难看,这时候就需要使用适当的窗函数,以满足我们工程测量的需要。
4、示波器中的 FFT 运算,不加窗和加矩形窗是一回事。
5、窗函数会改变频域波形,让频谱形成人们“喜欢”的形状,但是不会本质上消除频谱泄露,不同的窗函数都有其独特的特性,我们只需要根据工程测试的需要,选择一款合适的就可以了。
27.9 窗函数选择指南
如果在测试中可以保证不会有泄露的发生,则不需要用任何的窗函数(在软件中可选择 uniform)。
但是如同刚刚讨论的那样,这种情况只是发生在时间足够长的瞬态捕捉和一帧数据中正好包含信号整周期的情况。
如果测试信号有多个频率分量,频谱表现的十分复杂,且测试的目的更多关注频率点而非能量的大小。在这种情况下,需要选择一个主畔够窄的窗函数,汉宁窗是一个很好的选择。
如果测试的目的更多的关注某周期信号频率点的能量值,比如,更关心其EUpeak,EUpeak-peak,EUrms或者 EUrms2,那么其幅度的准确性则更加的重要,可以选择一个主畔稍宽的窗,flat -top 窗在这样的情况下经常被使用。
如果被测信号是随机或者未知的,选择汉宁窗。
27.10 总结
本章节的内容非常值得初学者看,如果你是初学者的话,建议认真的多看几遍。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号