transformer论文解读

• 1. 相关工作
• 2. 模型架构
• 3. 如何理解 Layer Norm
• 4. Encoder 和 Decoder 结构
• 5. 从 attention 到 Scaled Dot-Product Attention
• 6. Multi-Head Attention
• 7. Transformer 的三个 multi-head attention 的原理和作用
• 8. Embedding 和 Softmax 层
• 9. Positional Encoding
• 10. 为什么使用 self-attention!
• 参考资料

1. 相关工作

CNN 的的卷积核窗口大小有限，每次只能看比较短的部分序列，但是它的多通道机制被认为可以去识别多模式，transformer 论文参考这个机制，在 attention 的机制进一步引出了 Muti-Head Attention，来模拟卷积层的多输出通道效果。

Self-attention 在 transformer 论文之前已经有人提出，但 transformer 是第一个只依赖自注意力机制(self-attnetion)来实现 encoder-decoder 架构的模型。

2. 模型架构

（直到 GPT 出来之前）大多数有竞争力的神经序列转换模型都是采用编码器-解码器结构，transformer 模型也不例外。

编码器将输入的符号表示序列 (\(x_1,x_2,…,x_n\)) 映射为一个连续表示序列 (\(z_1,z_2,…, z_n\))。得到编码器输出序列 \(z\) 后，解码器逐个元素的生成符号的输出序列 (\(y_1,y_2…,y_m\))。解码器输出是自回归的，将当前轮的输出和输入拼接，作为下一轮的输入。

Transformer 的基本组件是: point-wise、self-attention、add & norm、feed forward、linear、softmax。

为了方便残差连接，模型中的所有子层 Sub Layer 以及嵌入层 Embedding Layer 都生成维度为 \(d_{model} = 512\) 的输出向量。

3. 如何理解 Layer Norm

NLP/Transformer 模型的输入是三维向量，batch、句子序列长度 \(n\)、单词映射为 embedding vector 都分别表示为一个维度。

Batch norm 和 layer norm 的区别一句话总结就是 bn 是切特征，ln 是切样本。

• BN: 对于每个特征维度，计算它在整个批次中的均值和标准差，然后对该特征进行归一化。
• LN: 对每个样本单独计算其所有特征的均值和标准差，然后在该样本内进行归一化。

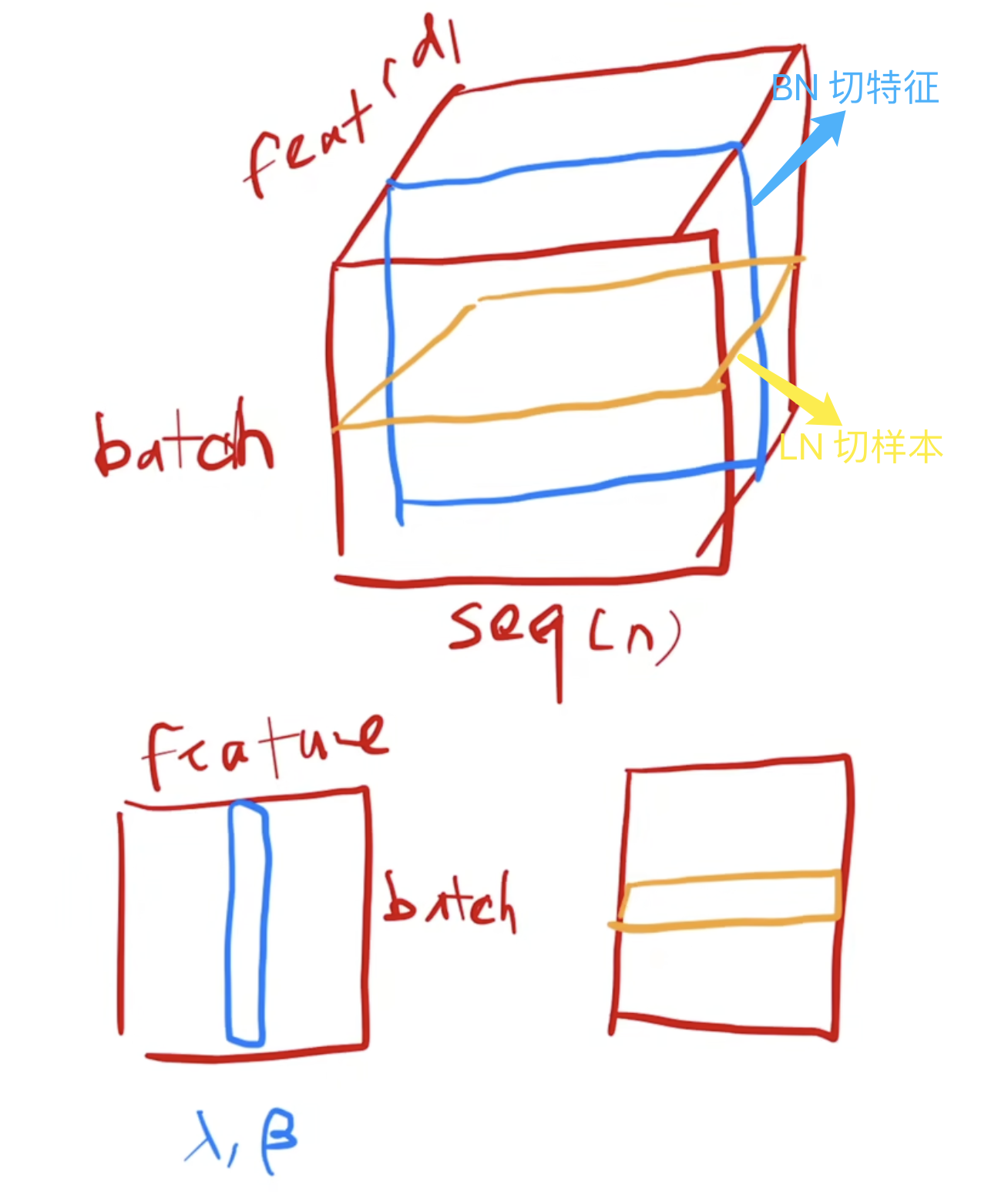
Layer Norm 层的计算可视化如下图所示:

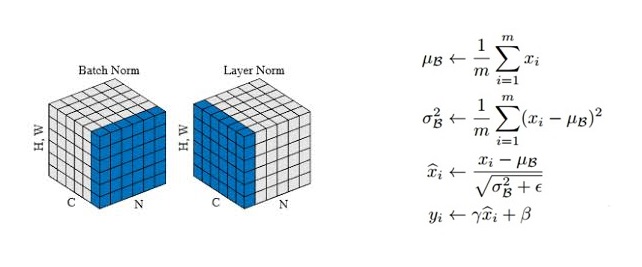
4. Encoder 和 Decoder 结构

Decoder 同样由 \(N = 6\) 个相同的层组成。Decoder 的 attention 是带掩码的，确保位置 \(i\) 的预测只能依赖于小于 \(i\) 的已知输出。

5. 从 attention 到 Scaled Dot-Product Attention

标准自注意力的数学表达式如下：

\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V \]

1，首先，注意力函数可以描述为将一个查询（query）和一组键-值对（key-value pairs）映射到一个输出 output，\(q\)、\(k\)、\(v\) 都是向量。输出都是对 value 进行加权求和得到的，每个 value 对应的权重 weight 是通过 \(q\) 和 \(k\) 之间的相似度计算得到。

2，将 q 和 k 的内积作为相似度（Dot-Product），然后除以向量的长度 \(\sqrt{d_k}\)（Scaled），结果再应用 softmax 函数，就会得到 \(n\) 个非负且相加求和等于 \(1\) 的权重向量，最后将权重应用于 value，就得到了最终输出 output。

余弦相似度常用来比较两个向量的相似度（距离），伪代码如下：

CosineSimilarity = sum(x[i]*y[i])/(sqrt(sum(x[i]*x[i]))*sqrt(sum(y[i]*y[i])))。

实际中，为了方便计算，会同时对一组查询（queries）计算注意力函数，将 q、k、v 都是构建成矩阵 \(Q\)、\(K\)、\(V\)（ 维度相等），涉及到两个矩阵乘法。

作者提到当向量维度变大的时候，softmax 函数会造成梯度消失问题，所以设置了一个 softmax 的 temperature 来缓解这个问题。这里 temperature 被设置为了 \(\sqrt{d_k}\)。

作者提出的注意力机制算法跟之前的 Dot-Product Attention 相比就是单纯多了 Scaled（除以 \(\sqrt{d_k}\)）。

另外 decoder 模块的 attention 多了一个 Mask，实际是第 \(t\) 时刻的 \(q\) 只能看前面阶段的对应的 \((k, v)\) 对，计算当中表现就是对于 \(q_t\) 和 \(k_t\) 及其之后的那些权重值都替换成一个极大的负数，这样经过 softmax 后（做指数 \(e^{w_t}\)），对应位置的 \(v\) 就变成了 0。

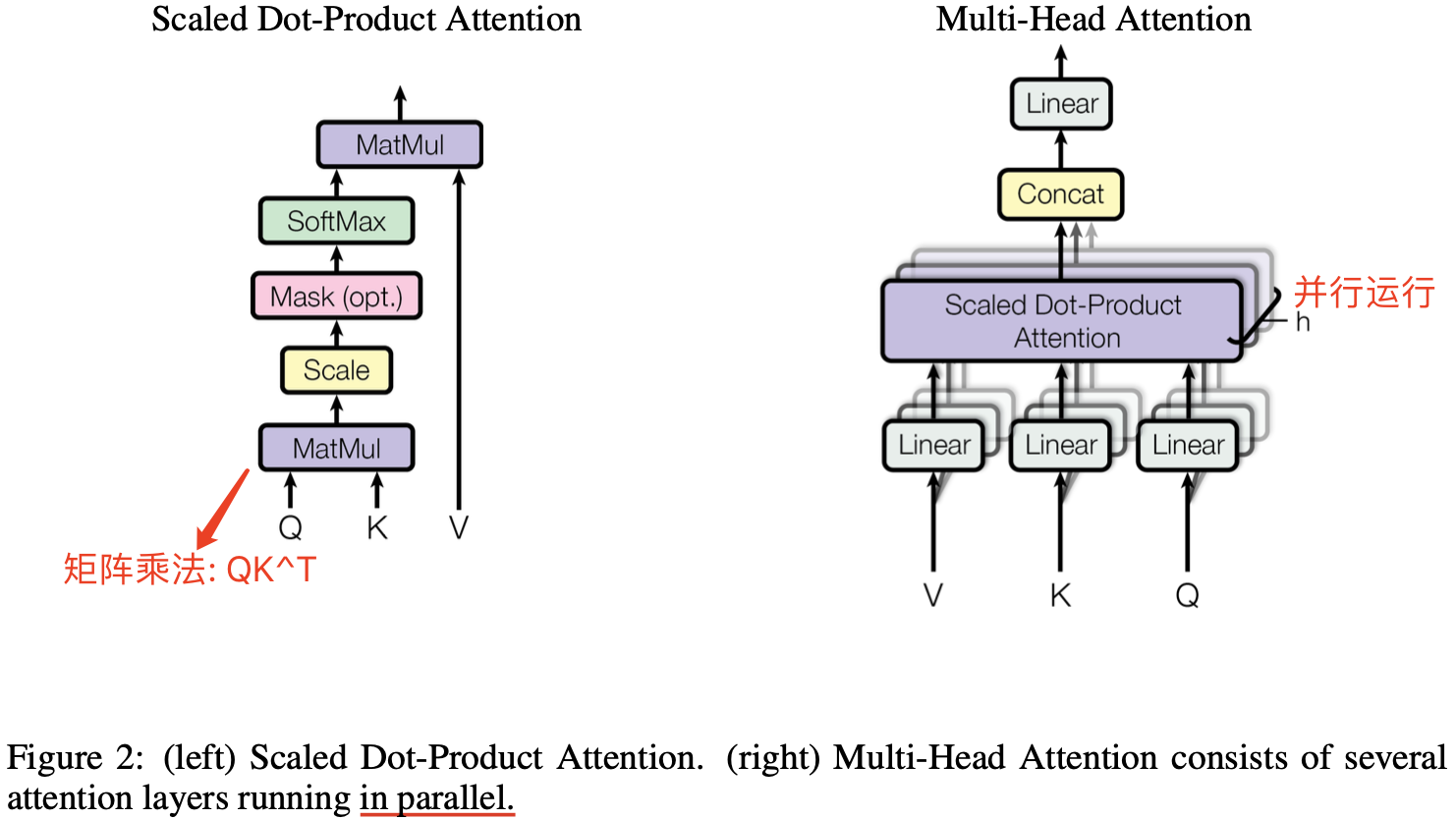
6. Multi-Head Attention

Scaled Dot-Product Attention 是不带任何参数的！

与其做单个的注意力函数，不如将 \(Q\)、\(K\)、\(V\) 投影到一个低维度、投影 \(h\) 次，然后再做 \(h\) 次的自注意力函数，并将这 \(h\) 个函数的输出拼接在一起，最后再次进行线性投影回来。

\[\text{Multi-Head Attention} = Concat(head_1,….,head_h) W^o \\ \text{Where} \ \text{head}_i = Attention (QW_i^Q, KW_i^K, VW_i^V)\]

\(Q\)、\(K\) 的线性(映射)层的权重维度是 \([d_\text{model}, d_k]\)，\(V\) 的线性(映射)层的权重维度是 \([d_{model}, d_v]\)，输出线性(映射)层权重维度是 \([h*d_v, d_{model}]\)。

作用：多头注意力机制可以注意到不同子空间的信息，捕捉到更加丰富的特征信息，实现类似卷积核的多通道机制的效果。

7. Transformer 的三个 multi-head attention 的原理和作用

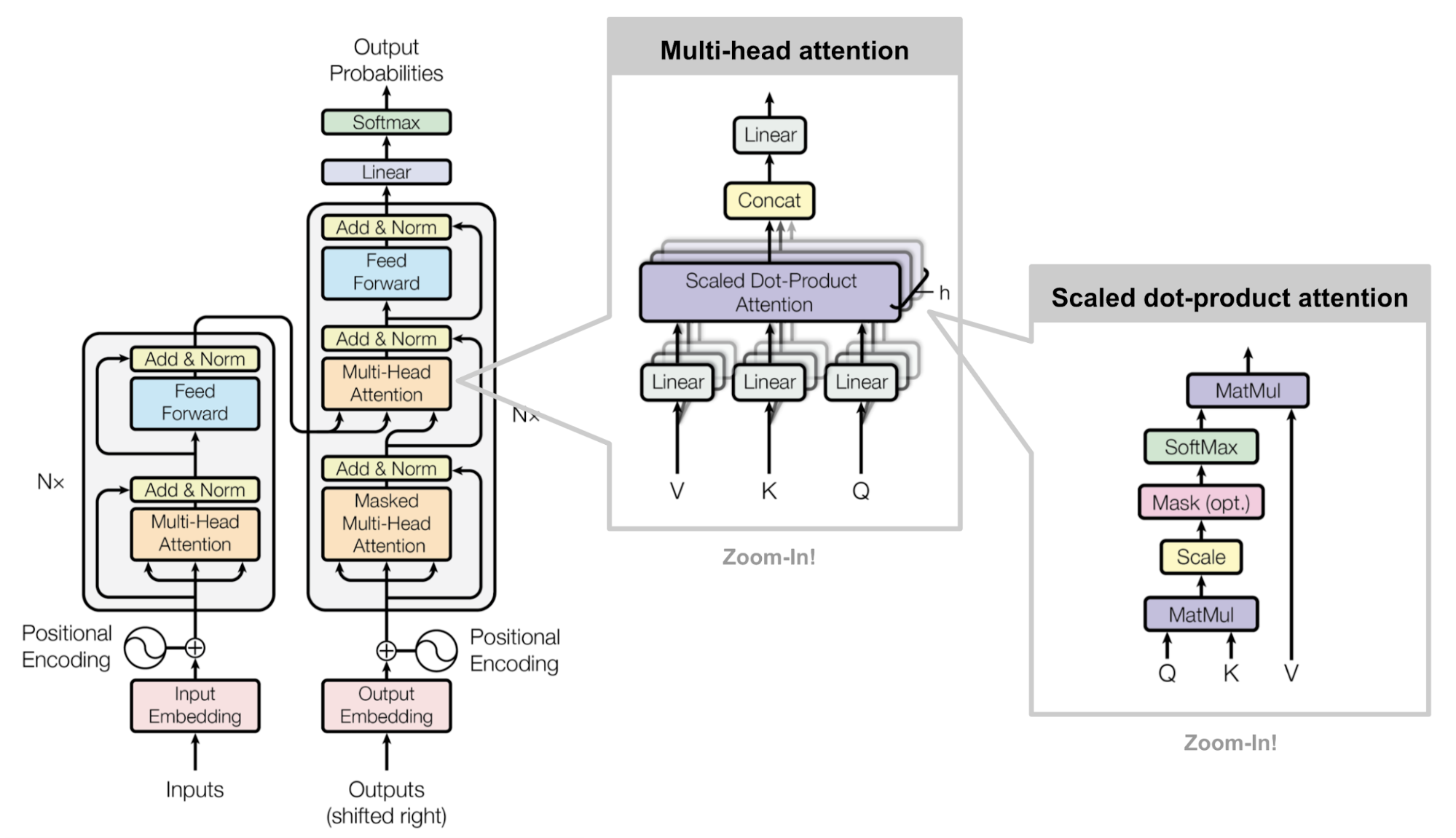
原理：

1. 解码器中的第二个注意力层，其查询 \(q\) 来自前一层的解码器层，但 \(k\)、\(v\) 来自于编码器最后一层的输出。
2. 编码器第一个注意力层：不考虑多头和线性投影层的情况，三个输入 \(q\) \(k\) \(v\) 本质上都是一个东西，三个输入都是原始输入本身自己，输出就是输入本身的加权和，而权重又来源自己本身跟跟各个向量的相似度函数，所以也叫自注意力层（self-attention）。
3. 解码器的第一个注意力层：编码器的最终输出作为 key value 输入进来，解码器下一层的输出作为 query 输入进来。

作用：

1. Self-Attention (自注意力)：对于每个位置上的 token，Self-Attention 将其与序列中的所有其他位置进行关联，从而使模型能捕捉到句子内部的语义关系。
2. Encoder-Decoder Attention (编码器-解码器注意力)：允许解码器在生成下一个词时参考编码器的输出。这种机制实现了输入和输出序列之间的联系，是实现翻译等任务的关键所在。
3. Masked Self-Attention (掩码自注意力)：过掩码机制屏蔽掉序列中未来位置的 tokens，从而确保模型预测生成的每个 token 仅依赖于当前生成位置之前的 tokens。

从 nlp 角度理解 Attention + MLP: Attention 负责从全局的角度把整个序列的信息聚合起来(捕捉上下文信息 + 信息聚合)，然后用 MLP 做语义的转换。

8. Embedding 和 Softmax 层

Embedding 层的作用学习一个长为 \(d_{model}\) 的向量来表示 token，编码器和解码器的输入都需要 embedding 层，两个嵌入层和 softmax 之前的线性变换之间共享相同的权重矩阵重（维度都是一样的），并且将权重值乘以 \(\sqrt{d_{model}}\)。

学习 embedding 时，可能会把每个向量的 \(\text{L2\ norm}\) 学得相对较小（维度越大权重值越小），乘以 \(\sqrt{d_{model}}\) 后放大，使得和 PE 相加时在 scale 上匹配。

L2 归一化（L2 Norm）是一种将向量缩放到单位长度的操作，使得向量的模为1。对于一个给定向量 \(\mathbf{v}\) ，L2 归一化后的向量 \(\mathbf{\hat{v}}\)，计算公式如下：

\[\mathbf{\hat{v}} = \frac{\mathbf{v}}{\|\mathbf{v}\|_2} \]

9. Positional Encoding

Attention 层的输出本身是不具备时序信息的，因为其本质是 value 向量的一个加权和，而权重是 query 和 key 的距离，跟序列信息无关。把输入 tokens 位置打乱，attention 的输出向量的所有元素的值大小不会变化，只有元素位置的变化，这显然不符合直觉。

而 Position encoding 层的作用是使得生成的 embedding vectors 值跟位置相关（加入时序信息），更符合人类文字的意义（文字的位置打乱，相应语义肯定会变化）。它的做法是将位置信息编码为向量，并将这些向量加到输入的嵌入向量中。Positional Encoding 通常通过以下公式计算：

\[PE(pos, 2i) = \sin \left(pos/10000^{2i/d}\right) \\ PE(pos, 2i+1) = \cos \left(pos/10000^{2i/d}\right)\]

10. 为什么使用 self-attention!

比较了四种不同的层： self-attention、rnn、cnn、self-attention (restricted)，分别比较了计算复杂度FLOPs、顺序操作（并行度）、最大路径长度。

参考资料

• 李沐读论文-transformer