机器学习的数学基础【线性代数篇】

1 长度的定义

1.1 范式(Norm)与长度

范式是一个将数据从N维空间中映射到一维实数空间内的函数，范式是计算向量长度的规则，经由范式求解出的实数就是某一范式下对应的实数，它满足以下三个条件：

长度值大于等于0，当长度为0的时候，范式的输入x必定也为0
两变量和的范式小于等于两变量范式的和
数乘运算的可脱性

1.2 范式的几种变体

以下是范式的四种变体，最右侧展示的是每一种范式的条件下，二维空间内单位圆的可视化图像。圆包括圆心和半径，半径到圆心距离（长度受范式定义变化的影响，因此其形态与常规认知的单位圆有差别）相等的点构成的集合是圆，无论形态怎么样，只要满足该定义的几何图形就是圆。

2.1 Positive Definite Matrices(正定矩阵)

正定矩阵: 对于一个$n \times n$的实值对称矩阵 $ M $，如果对于所有的非0向量 $ z \epsilon \mathbf{R}^n $ 都满足 $z^{\top}Mz>0$，那么该矩阵就是一个正定矩阵。
特性：
$ M $ 的特征值 $ \lambda $是一个正值。
存在一个下三角矩阵 $ L $, $ L $ 中的每个元素都大于0，并且 $ L $ 中的各列严格正交，可以将 $ M $进行分解， $ M = L^{\top}L $ 这叫cholesky decomposition，克列斯基分解。

2.2 Eigenvalues and Eigenvectors(特征值和特征向量)

2.2.1 定义

对于给定的一个线性变换(从空间V转换到空间V)A，如果非零向量 $ x $ 满足特征方程：
$ Ax = \lambda x $ ，其中 $ \lambda $ 是标量。 $ \lambda $被称为线性变换 $ A $ 对应于 x 的特征值。

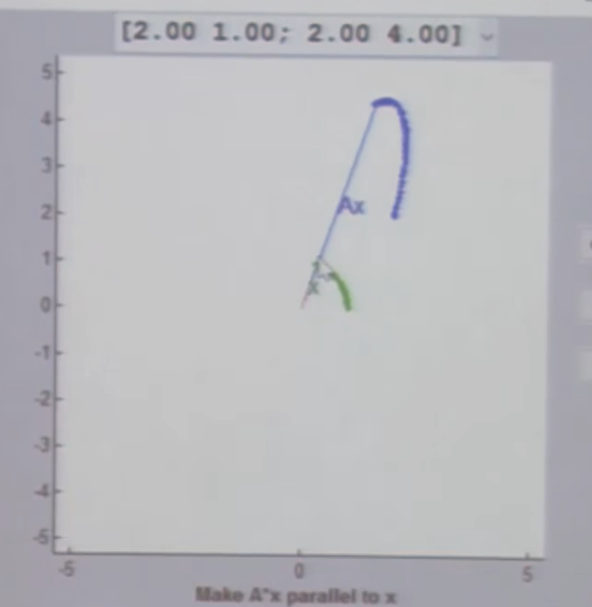
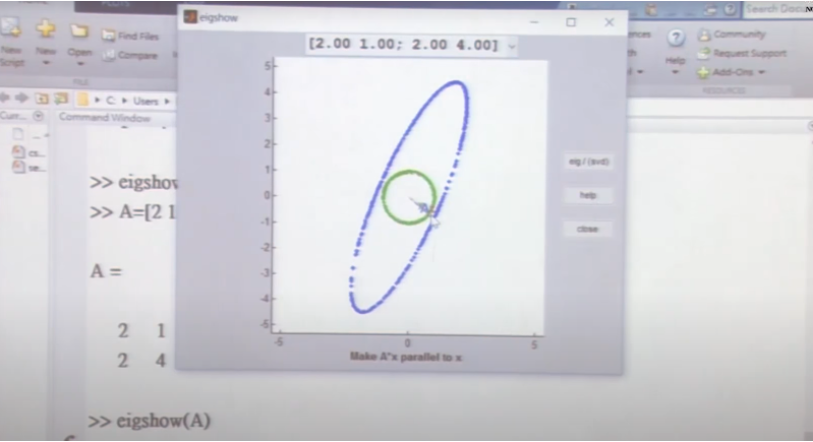
2.2.2 可视化

实际上，特征值以特征向量为核心，当我们定义好向量的模时，以该向量的端点画圆，会发现，特征值、线性变化A、特征向量之间仅在椭圆的长轴和短轴处产生这种联系，特征向量指示的方向，为椭圆的长短轴方向。

2.3 Diagonalization（矩阵的对角化）

对于一个矩阵 $ A_{n \times n} $ ， $ {\lambda}1 , \lambda_2,..., \lambda_n $ 是它的特征值， $ q_1, q_2, ..., q_n$是它的n个特征向量，则矩阵 $ A $ 可以被对角化为: $ A $ = $ Q \Lambda Q^{\top} $,其中特征向量就是主成分。