LeetCode(119):杨辉三角 II
Easy!
题目描述:
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 3 输出: [1,3,3,1]
进阶:
你可以优化你的算法到 O(k) 空间复杂度吗?
解题思路:
杨辉三角想必大家并不陌生,应该最早出现在初高中的数学中,其实就是二项式系数的一种写法。
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1
杨辉三角形第n层(顶层称第0层,第1行,第n层即第n+1行,此处n为包含0在内的自然数)正好对应于二项式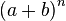 展开的系数。例如第二层1 2 1是幂指数为2的二项式
展开的系数。例如第二层1 2 1是幂指数为2的二项式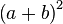 展开形式
展开形式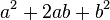 的系数。
的系数。
杨辉三角主要有下列五条性质:
- 杨辉三角以正整数构成,数字左右对称,每行由1开始逐渐变大,然后变小,回到1。
- 第
 行的数字个数为
行的数字个数为 个。
个。 - 第
 行的第
行的第 个数字为组合数
个数字为组合数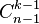 。
。 - 第
 行数字和为
行数字和为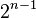 。
。 - 除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和(也就是说,第
 行第
行第 个数字等于第
个数字等于第 行的第
行的第 个数字与第
个数字与第 个数字的和)。这是因为有组合恒等式:
个数字的和)。这是因为有组合恒等式: 。可用此性质写出整个杨辉三角形。
。可用此性质写出整个杨辉三角形。
由于题目有额外限制条件,程序只能使用O(k)的额外空间,那么这样就不能把每行都算出来,而是要用其他的方法,。最先考虑用的是第三条性质,算出每个组合数来生成第n行系数,代码如下:
C++ 解法一:
1 /** 2 * NOT Correct! 3 */ 4 class Solution { 5 public: 6 vector<int> getRow(int rowIndex) { 7 vector<int> out; 8 if (rowIndex < 0) return out; 9 10 for (int i = 0; i <= rowIndex; ++i) { 11 if ( i == 0 || i == rowIndex) 12 out.push_back(1); 13 else 14 out.push_back (computeCnk(rowIndex, i)); 15 } 16 return out; 17 } 18 19 int computeCnk(int n, int k) { 20 if (k > n) return 0; 21 else if (k > n/2) k = n - k; 22 int numerator = 1, denomator = 1; 23 for (int i = 0; i < k; ++i) { 24 numerator *= n - i; 25 denomator *= k - i; 26 } 27 if (denomator != 0) return numerator/denomator; 28 else return 0; 29 } 30 };
本地调试输出前十行,没啥问题,拿到OJ上测试,程序在第18行跪了,中间有个系数不正确。那么问题出在哪了呢,仔细找找,原来出在计算组合数那里,由于算组合数时需要算连乘,而整形数int的数值范围只有-32768到32768之间,那么一旦n值过大,连乘肯定无法计算。而丧心病狂的OJ肯定会测试到成百上千行,所以这个方法不行。那么我们再来考虑利用第五条性质,除了第一个和最后一个数字之外,其他的数字都是上一行左右两个值之和。那么我们只需要两个for循环,除了第一个数为1之外,后面的数都是上一次循环的数值加上它前面位置的数值之和,不停地更新每一个位置的值,便可以得到第n行的数字。
C++ 解法二:
1 class Solution { 2 public: 3 vector<int> getRow(int rowIndex) { 4 vector<int> out; 5 if (rowIndex < 0) return out; 6 7 out.assign(rowIndex + 1, 0); 8 for (int i = 0; i <= rowIndex; ++i) { 9 if ( i == 0) { 10 out[0] = 1; 11 continue; 12 } 13 for (int j = rowIndex; j >= 1; --j) { 14 out[j] = out[j] + out[j-1]; 15 } 16 } 17 return out; 18 } 19 };





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 终于写完轮子一部分:tcp代理 了,记录一下
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理